“字节跳动-文远知行杯”广东工业大学第十四届程序设计竞赛——解题报告
前言:
Easy:A B C G
Medium:H J
Hard:D E F I
最近要忙一些别的事,等有空了再继续补全。
A:hzy 和zsl 的挑战
其中A是签到题,因为他们“足够聪明”,又因为每次只有两种可能的答案,所以他们可以采取一定的策略使得百分百得到答案。所以输出4个1.00即可。
B:人类史上最大最好的希望事件
这个题目主要难在题意理解上,本质上是求斐波那契平方前缀和。再来看题意:
“如果我们以四分之一圈为单位,那么我们用类似带分数的形式表示螺旋线转动的起点和终点。例如,0+0 到 0 + 1 意即从第一个方格转到第二个方格,划过了前两个方格,他们的面积之和为2(1+1)。同理,0+0 到 1+0 划过了前五个方格,他们的面积之和为40(1+1+4+9+25)。”
从最里面最小的矩形开始看,题意来看它是第1个矩形,那么a+b位置的矩形方格其实就是第4*a+b+1个矩形。(按照螺旋曲线由内向外数)所以题意就是问从第a+b个矩形到第c+d个矩形的面积和,而由于第一个和第二个矩形是边长为1的正方形,所以所求即斐波那契数列平方和。
既然读懂了题意,就会发现本题就是简单的求前缀和,而数据又小,因此前缀和完全可以解决。不过有个求斐波那契平方和的公式:
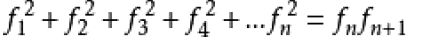
代码示例:
#include
using namespace std;
const int maxn = 60000;
typedef long long ll;
const ll M = 192600817;
ll f[maxn],fib[maxn];
int main(){
int q;
fib[1] = fib[2] = 1;
for(int i = 3;i < maxn;i++) fib[i] = (fib[i-1]+fib[i-2])%M;
f[1] = 1;
f[2] = 2;
for(int i = 3;i < maxn;i++){
f[i] = (f[i-1] + fib[i]*fib[i]%M)%M;
}
while(cin >> q){
while(q--){
int a,b,c,d;
cin >> a >> b >> c >> d;
int x = 4*a+b+1;
int y = 4*c+d+1;
//cout << x << " "<< y << " ";
if(x > y) swap(x,y);
cout << (f[y] - f[x-1]+M)%M << endl;
}
}
return 0;
}
代码示例2:
#include
using namespace std;
const int maxn = 60000;
typedef long long ll;
const ll M = 192600817;
ll fib[maxn];
int main(){
int q;
fib[1] = fib[2] = 1;
for(int i = 3;i < maxn;i++) fib[i] = (fib[i-1]+fib[i-2])%M;
while(cin >> q){
while(q--){
int a,b,c,d;
cin >> a >> b >> c >> d;
int x = 4*a+b+1;
int y = 4*c+d+1;
//cout << x << " "<< y << " ";
if(x > y) swap(x,y);
cout << (fib[y]*fib[y+1]%M-fib[x]*fib[x-1]%M+M)%M << endl;
}
}
return 0;
}
C:超级无敌简单题
本题 k < 150000,而我们实际上判断一个“鸽子数”所需要不过八次循环,所以暴力是可以解决的。但(详情请百度happy number)实际上只要我们在计算过程中出现4这个数子,那么这个数就一定不是”鸽子数“,所以我们可以根据这一点来简化判断。
代码示例:
#include
#include
using namespace std;
const int maxn = 160000;
int f[maxn];
int cnt = 0;
bool check(int x){
while(x != 1 && x != 4){
int t = 0;
while(x)
{
t += (x % 10) * (x % 10);
x /= 10;
}
x = t;
}
return x == 1;
}
void init(){
for(int i = 1;cnt < maxn;i++){
if(check(i)) f[++cnt] = i;
}
}
int main(){
int q;
scanf("%d",&q);
init();
while(q--){
int k;
scanf("%d",&k);
printf("%d\n",f[k]);
}
return 0;
}
D:免费送气球
E:水题
F:清一色
G:简单数学题
这题据说是套路题,老师说是常见套路。我先给出题解文件中的公式化简:
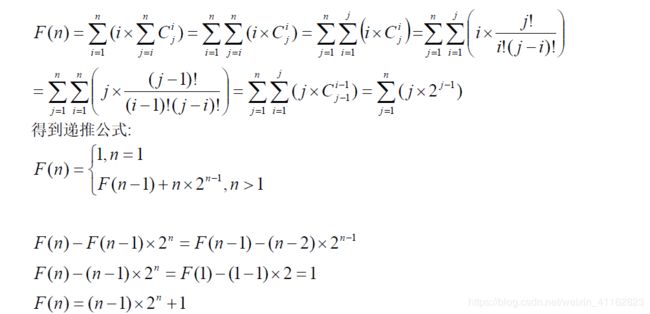
看到了吧,主要是化简公式。上面说的常见套路体现在第二步到第三步,注意这里 i 和 j 的变化,为什么可以这样我也不知道,既然是常见套路那么下次遇到类似的就往这方面思考就好了。
代码示例:
既然公式都推出来了,接下来就是快速幂了。
#include
using namespace std;
const int M = 1000000007;
typedef long long ll;
ll qpow(ll a,ll b){
ll res = 1;
while(b){
if(b&1) res = res*a%M;
a = a*a%M;
b >>= 1;
}
return res;
}
int main(){
ll n;
while(cin >> n){
cout << ((n-1)%M*qpow(2,n)%M+1)%M << endl;
}
return 0;
}
H:zyb的面试
这题似乎是某个面试题。首先题意很好理解,将1~n的数字按照字典序排列,我们可以考虑建立一颗十叉树(???)。简单的说就是每个根有十个子节点(0,1,2,…,9),像这样不断建立到n;这样bfs得到的就是自然序,dfs得到的则是字典序。但是这样遍历会超时,所以需要剪枝一下,很显然,我们可以根据k来确定它所处的深度以及位置。
I:故事
J:Count
这题我比赛时的思路是求通项公式,求了俩小时后我哭了,然后放弃了。我后来转念一想这说不定可以用矩阵加速链乘,但奈何本人做题少,不会总结转移矩阵(说白了是不会分解n3。但实际上转移矩阵与目标矩阵如下:
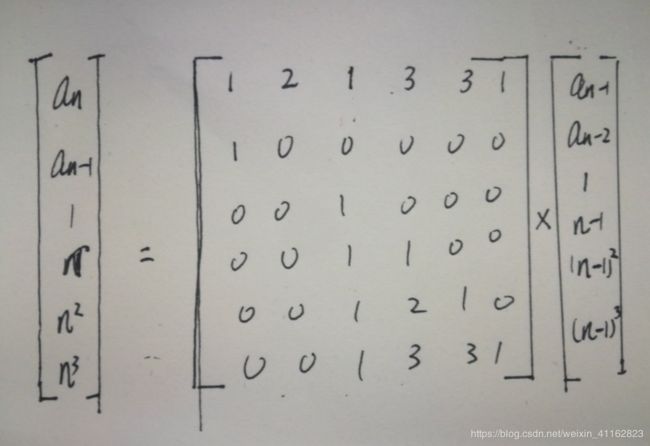
如此一来就可以用矩阵加速链乘来做了。(即矩阵快速幂)
代码示例:
由于测试矩阵是否正确的代码没有删去,所以略显累赘,但真正需要思考的代码不过四五十行以内。(主要是实现矩阵)
#include
#include
#include
using namespace std;
const int M = 123456789;
typedef long long ll;
struct Matrix{
ll v[10][10];
int n;
Matrix(int n):n(n){}
void init(){
for(int i = 0;i < n;i++)
for(int j = 0;j < n;j++) v[i][j] = 0;
}
Matrix operator *(const Matrix b) const {
Matrix C(n);
C.init();
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
for(int k = 0;k < n;k++){
C.v[i][j] = (C.v[i][j] + v[i][k]*b.v[k][j]%M)%M;
}
}
}
return C;
}
void qpow(ll x){
Matrix C(n);
C.init();
for(int i = 0;i < n;i++) C.v[i][i] = 1;
while(x){
if(x&1) C = C*(*this);
*this = *this*(*this);
x >>= 1;
}
*this = C;
}
void print(){
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
cout << v[i][j] << " ";
}
cout << endl;
}
}
};
ll f(ll x){
Matrix A(6);
A.init();
A.v[0][0] = 1; A.v[0][1] = 2;
A.v[0][2] = 1; A.v[0][3] = 3;
A.v[0][4] = 3; A.v[0][5] = 1;
A.v[1][0] = 1; A.v[2][2] = 1;
A.v[3][2] = 1; A.v[3][3] = 1;
A.v[4][2] = 1; A.v[4][3] = 2;
A.v[4][4] = 1; A.v[5][2] = 1;
A.v[5][3] = 3; A.v[5][4] = 3;
A.v[5][5] = 1;
// A.print();
Matrix B(6);
B.init();
B.v[0][0] = 2; B.v[1][0] = 1;
B.v[2][0] = 1; B.v[3][0] = 2;
B.v[4][0] = 4; B.v[5][0] = 8;
// B.print();
A.qpow(x-2);
Matrix C(6);
C = A*B;
// C.print();
cout << C.v[0][0] << endl;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
ll x;
scanf("%lld",&x);
f(x);
}
return 0;
}