KMP算法

一、字符串匹配场景

KMP算法可以解决以字符串匹配为模型的问题，算法应用场景非常广泛，并不仅仅限于文本的匹配。

以简单的字符串匹配为例，现有两个链分别为source和target，

要在Source链中匹配Target链，很容易观察出出从source链下标10的位置可以成功匹配，如下图所示：

 

二、非KMP算法对此类问题的求解方式

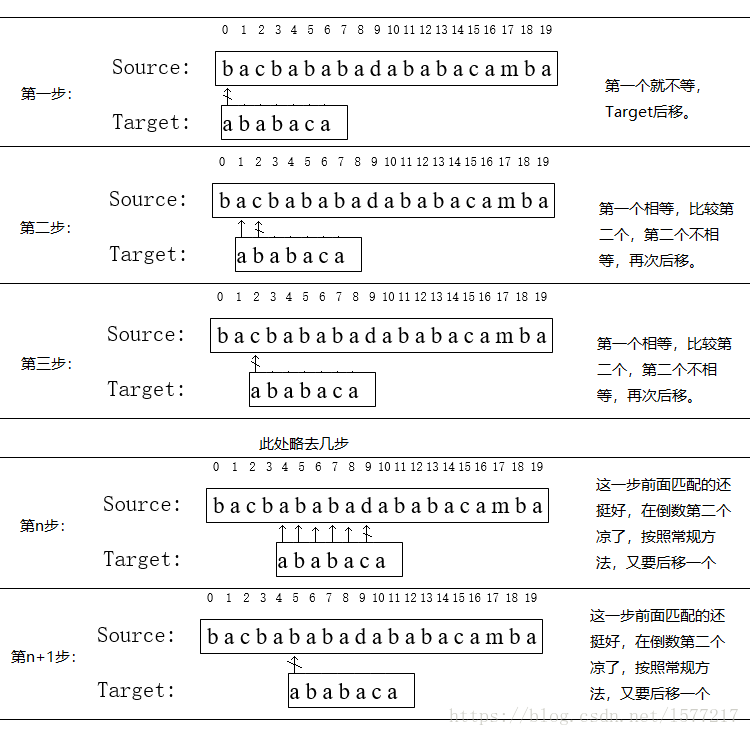
在字符串匹配问题中，最直观的想法就是，Source链保持不动，Target链从开始位置每次向后滑动一个字符长度，在该位置上按照字符对齐的位置逐个与Source链上的字符进行比较，若Target链上的所有字符在该位置均可以与Source链上对齐位置的字符成功匹配，则匹配结束，若失败，则Target链向后滑动一个字符长度，继续按照字符对齐位置逐比较，用一张图来表示该过程：

按照此方法，直到在Source下标为10处完成匹配，这养的复杂度是O（m*n）。

现在分析第n步和第n+1步，在第n步中，已经匹配了5个字符:ababa，但是因为c与d不相等，匹配失败，第n+1步Target链后移一个单位，从头开始匹配。

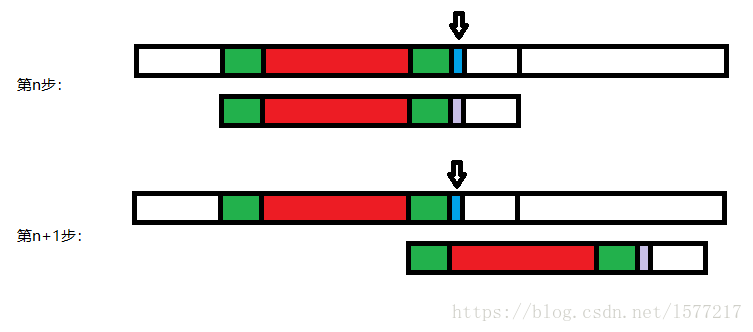
在匹配过程中，Target字符串的前5个字符已经被遍历并成功匹配，我们期望这5个字符串中有一些可以用于优化下一次匹配的信息，来看另一种第n+1步的做法：

按照最开始的思路继续运行，在多进行几步后，也可以到达上图中的状态，而且中间一定不存在成功匹配的情况，也就是说，如果按照最开始的方法，上图中的匹配场景一定会到达，从第n步到优化后的第n+1步，既省略了好几趟没有成功的比较，又可以不从Target下标为0的位置开始。优化过程利用了Target链本身的一些性质，KMP算法就是充分利用这些特性，下面就来分析这些特性！

三、KMP算法原理

首先说优化的目标：减少比较的次数，那么该怎么减少呢？先来个直观一些的：颜色一样的是相同的，第n步在箭头指向的位置匹配失败，下一步进行第n+1步：

这个图并不能很好的表示，原因有两个：第一，匹配过程中source链本身是不可知的，应该完全依靠Target链的信息；第二，能匹配的部分一定是相等的，在source链上再画出是多余的，改完之后（强调：第n步箭头位置标示匹配失败的地方，第n+1步箭头位置标示待匹配的地方）：

如果这两张图能看明白，那KMP的主要思想应该就懂了，关注点就在Target链上这种绿色的结构。

3.1字符串的特性分析

我们都知道，在匹配过程中，如果某次节点比较发现不相等，那么是一定需要回退的，只是回退多少的问题，但优化后可以减少比较的次数，像上面优化的第n+1步，相比于原来的比较方式，就可以很大程度上减少比较次数。

在进行分析前，我们可以先思考一下，什么情况下，在某个元素匹配失败后，不用全部回退，很容易想到，那就是在target串中有重复的子串，假如他们从左到右分别叫为substr1，substr2，并且substr1和substr2完全相等。

那么当我们开始考虑回退多少时，有一件事一定已经发生，那就是substr2后面紧接着的一个节点匹配失败了（这里的subStr2可以为空串，此处并不失一般性），这时候substr2已经完成了匹配，那么substr2的位置一定可以成功匹配substr1，那在接下来的比较中，不就可以直接跳过这一部分的比较了？但这里有一个条件，substr1必须是从下标为0的位置开始的，不难想象这个条件，如果不从0开始，那在substr1之前的节点是无法保证一定能匹配到substr2前面紧挨着的节点上的。

在直观上了解原理后，就要想办法把这些特性表示出来，然后用到代码里，首先，要做一个定义：

对于任意一个字符串，存在相等的最长前缀和最长后缀，说白了就是在一个字符串中，从下标为0的位置开始的一个子串（不包含最后一个字符）和从后面某位置开始的一个子串（一定要包含最后一个字符）相等，那么这两个子串分别就是相等最长前缀和最长后缀，下面列举一些例子，左边是字符串，右边是最长前缀和最长后缀：

只有一个字母的时候就是空串“”，在此基础上，为了实现我们的算法，需要的就是根据当前刚刚匹配失败的位置，想办法得到一个能够控制回退的值，也就是说已经成功匹配的那部分字符串中，包含着最优的回退方法，在KMP中，用一个整数来描述最优的回退的值，习惯把这些值存在名为next的数组中，针对上面的示例，得到next数组存储结果是：

这里-1表示不存在，0表示存在长度为1，2表示存在长度为3，这是为了和代码相对应（好多程序员写的书都是从第0章开始。。），也就是说next数组长度和Target数组长度一致，next[i]就表示Target[0:i]子串的最长前缀的长度值减一，这里next[i]的值一定小于i。

再回头看下我们之前匹配失败的第n步，假设i，j分别为当前比较的节点的下标，即i=9，j=5。

在这一步中，Target[5]匹配失败了，但是我们知道，Target[0~2]与Target[2~4]是相等的，此时Target[2~4]与Source[6~8]是成功匹配的，所以Target[0~2]也一定可以和Source[6~8]成功匹配，而无需再做多余的匹配，那么下一步i，j的值就可以根据这个进行相应的变换，i=9，j=3，有没有发现什么规律？在成功匹配的那部分子串ababa中，next值为2，j=2+1，到这应该就明白了，j=0,j=1,j=2那部分就是我们说的不用匹配的位置，直接从下一个位置开始就行了，所以j=2+1！。

 

3.2代码该如何实现呢？

如果到这里已经明白了大概的原理，那么接下来就可以看看别人的代码了>>_<<(别人的代码，还是各种骚操作，自己能能实现，但就显得有点复杂了，所以直接看优秀的代码吧。。。）

通过之前分析知道，KMP最重要的还是要依据待匹配字符串，也就是Target的特性，得到next数组，所以先从得到next数组开始,那next数组该怎么求呢，这里就有一个比较有意思的事情，求next数组本身又是一个字符串匹配的过程，所以在求next的过程中，可以用到已经求得的next值。

假设我们现在求next[i+1]，那么我么总希望结果是好的，那么什么算好的呢？在Target[0~i]中，存在相等最长前缀subStr1和最长后缀subStr2，两个长度都是m，最好的情况就是Target[m]=Target[i+1]，那next[i+1] = next[i] +1，举个例子：

在abcabc中求next[5]，那么此时已经得到的subStr1= subStr2 = ab，m=2，next[4] = 1，发现Target[2]与Target[5]相等，那么next[5]=next[4] + 1=2。

那如果情况不好怎么办？当发现Target[m]！=Target[i+1]时，我们可能还想继续偷懒：那把subStr2缩短一点吧，留下后面的部分，subStr1也变短点，留下前面那部分，但是保证变短后的两部分还是相等的，在进行同样的比较，不就又可以少比较几次了吗？那怎么实现呢，这部分也很有意思，我们来举个例子：

对于abacabad，假如我们要求next[7]，那么在Target[0:6]中，此时已经得到的subStr1= subStr2 = aba，m=3，next[6] = 2，发现Target[m]!=Target[7]，怎么缩短呢，subStr1自己有最长前缀和最长后缀，subStr2也有自己的最长前缀和最长后缀，那么我要开始说一句真理了：subStr1的最长前缀一定等于subStr2的最长后缀！为什么呢？因为subStr1等于subStr2，最长前缀等于最长后缀，这是一定成立的，放到例子中，subStr1的前缀是a，subStr2的后缀也是a，则m=1，此时比较Target[m]==Target[7]就可以了！接下来就来看下求next的代码：

public static int[] getNext(String target){
		int[] next = new int[target.length()];
		next[0] = -1; //一个字母的时候，不存在相等最长前缀和最长后缀，所以值为0；
		int k = -1;//若下一个待求位置是next[i+1],则k的初始值为next[i],因为next[0]是固定的，下一个待求位置是next[1]，所以k=next[0]=-1
		/**
		 * 这里更符合意义的写法是：
		 * int i = 0;
		 * next[i] = -1;
		 * int k = next[i];
		 * 直接给k=-1，如果不太理解过程就很难明白到底在干嘛，还有就是需要注意，k+1就等于我们上面谈到的m
		 */
		
		for(int i = 1; i < target.length(); i++){
			while(k > -1 && target.charAt(k + 1) !=  target.charAt(i)){ 
				//能运行到这里，就说明不是我们最希望的状况，而这个循环就是当状况不好时，退而求其次，“缩短”能偷得懒。
				//k > -1有两个作用，1是是防止访问越界2是k如果<=-1表示不存在最长前/后缀，就没有必要找了
				k = next[k];
			}
			//跳出循环有两种情况，一种是找到了一个缩短后能用的，一个就是k等于-1了
		if (target.charAt(k + 1) ==  target.charAt(i)){
	            k = k + 1;
	        }
			next[i] = k;
		}
		
		return next;
	}

 

有了next数组，那下面就好说了，因为在求next的过程中，我们一直在用KMP算法求next的值，在这里代码一般有两种具体的实现方式，一种是先得到next数组，在匹配，一个是一遍匹配一遍生成next数组。我们这里给出第一种实现。

 

public static int KMP(String target, String source){
		int next[] = getNext(target);
		int k = next[0];
		for(int i = 0; i < source.length(); i++){
			while(k > -1 && target.charAt(k + 1) != source.charAt(i)){
				k = next[k];
			}
			if(target.charAt(k + 1) == source.charAt(i)){
				k = k + 1;//成功匹配一个节点
			}
			if(k == target.length()-1){//上面一直说k等于已经匹配的长度-1
				return i - target.length() + 1;
			}
			
		}
		return -1;
	}

第一篇到此结束，参考博文：https://blog.csdn.net/starstar1992/article/details/54913261，如有疑问，欢迎大家交流分享。