动手学:线性回归学习笔记
新手写文写了自己的理解比较多,意在给自己看,不感兴趣的地方可能写的就随便一点,有错误请指出,伯禹学习平台学习笔记Task1。
动手学:线性回归学习笔记
模型
系统要学习的东西是一个线性关系。例如:房价 = k1面积 + k2房龄 + b,房价由面积和房龄两个因素造成,我们就是需要学习面积权重k1占多少,房龄k2占多少,和偏差值b。
数据集
我们如何让计算机学习到k1,k2和b呢,我们需要有数据集,数据集就是一堆数据的集合。让计算机学习就像教小孩一样,把例子和答案让它知道就行了(监督学习),例如如何让小孩子知道一个物体是苹果,就把苹果给他看告诉他这是苹果,把雪梨给他看这不是苹果,小孩子就会学习到苹果的模型,就是红色的,不规则形状的,例子里面给小孩子看的苹果和雪梨以及答案就是数据集。回到房价问题上,我们只要给足够的数据集就可以学习到房价
| 面积 | 房龄 | 房价 |
|---|---|---|
| 2 | 1 | 10 |
| 4 | 1 | 20 |
| … | … | … |
里面一行就是以一个样本,面积和房龄两个因素就是特征(苹果的样子特征,气味特征等等),房价就是标签(答案)。这是用来训练计算机学习模型用的数据集,就叫训练集。
损失函数
上面是比较直观的了解计算机如何学习模型,这里涉及到具体到细节计算机是如何学习的。损失函数是用来计算计算机预测的值和答案之间的误差(差距),因为计算机学习并不是一个样本就可以学习出来的,可以认为是一个理解能力有问题的小孩子,需要很多个样本,并且告诉他他现在学习到的东西离答案差多少,他就会一步步更改自身学习的内容(权重)来向答案靠近(想一想那个猜100以内的数字的游戏)。
损失函数就是用来计算计算机现在预测出来的值和真实值之间的误差的。一个常用于回归问题的损失函数就是平方函数,表达式为:w就是权重[k1,k2],b就是偏差
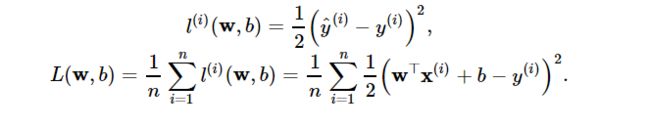
数学公式出现了,但是不要怕,我们是调参侠,我们受过专业的训练,无论多复杂的公式我们都不会怕。看一看公式,首先第一行是每个样本的损失函数计算公式,(预测值 - 真实值)^2 / 2 ,用这一条就可以算出计算机在预测这一个样本时得出的预测值和真实值的误差。但是我们一般都是从整体看差距,而不是一条条的看,所以我们使用下面的公式,这个公式就是如果数据集有n个样本,就把n个样本的损失值取平均值,公式可见n个损失值相加除以n。这样就得出现在阶段的损失值了。
优化函数 - 随机梯度下降
刚刚说了,计算机会根据误差来一步步修正自身的权重来靠近答案(标签),这是就是一个不断减小损失值的过程,具体如何修正呢?就是使用了优化函数。优化函数是用来更新自身权重的方法,学习了小批量随机梯度下降。小批量是什么意思呢?我们本来用的是批量梯度下降,使用全部样本的损失值的导数进行更新权重,而小批量的意思就是使用一部分样本的损失值的导数(梯度)进行权重更新。公式为:
B是小批量样本的数量,η 是学习率每次更新的大小。更新那个权重就使用损失函数对那个权重的偏导数进行计算。优化函数都有两个步骤,(1)初始化模型参数(权重)。(2)迭代,负梯度方向(所以用 - )多次更新参数。
Pytorch简易实现
导入包
torch.manual_seed为torch包设置随机种子
torch.set_default_tensor_type更改torch默认类型
import torch
from torch import nn
import numpy as np
torch.manual_seed(1)
print(torch.__version__)
torch.set_default_tensor_type('torch.FloatTensor')
生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
读取数据集
Data.DataLoader生成数据读取器,batch_size小批量数量
import torch.utils.data as Data
batch_size = 10
# combine featues and labels of dataset
dataset = Data.TensorDataset(features, labels)
# put dataset into DataLoader
data_iter = Data.DataLoader(
dataset=dataset, # torch TensorDataset format
batch_size=batch_size, # mini batch size
shuffle=True, # whether shuffle the data or not
num_workers=2, # read data in multithreading
)
定义模型
定义一层num_inputs × 1 的全连接层
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# other layers can be added here
)
print(net)
print(net[0])
定义损失函数
torch.nn.MSELoss为平方损失函数
loss = nn.MSELoss() # nn built-in squared loss function
# function prototype: `torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')`
初始化模型参数
使用torch.nn.init包进行模型参数的初始化
from torch.nn import init
init.normal_(net[0].weight, mean=0.0, std=0.01)
init.constant_(net[0].bias, val=0.0) # or you can use `net[0].bias.data.fill_(0)` to modify it directly
for param in net.parameters():
print(param)
定义优化函数
torch.optim里面包含各种优化函数,直接调用随机梯度下降SGD
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03) # built-in random gradient descent function
print(optimizer) # function prototype: `torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)`
训练
epochs为3,每迭代完整个数据集才算一个epochs。
训练顺序:预测,计算损失值,计算梯度,更新权重
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X) #预测
l = loss(output, y.view(-1, 1)) #计算损失值
optimizer.zero_grad() # reset gradient, equal to net.zero_grad()梯度清零,防止累加上次更新的梯度
l.backward() #计算梯度
optimizer.step() #更新权重
print('epoch %d, loss: %f' % (epoch, l.item()))
动手学:softmax回归与分类模型学习笔记
softmax回归
softmax回归作用在输出层通常用于分类问题,先看看不用softmax如何进行分类问题。一个三分类问题,类别猫=1,狗=2,猪=3,制作标签就是类别猫[1,0,0],狗[0,1,0],猪[0,0,1]。神经网络输出层三个神经元对应三个类别,那么就看哪个输出值大就认为这个样本属于这个类别,如输出10,50,30则该样本第二个神经元输出值50最大,则属于狗类别。这样做的问题是
1.输出值没有较为直观的意义,而且输出值的不确定范围比较大,
2.很难衡量与标签之间的误差。
所以我们需要用softmax作用于输出层解决这些问题。

softmax把输出层的值都转化为0-1范围的概率分布,这样每个输出神经元就等于对应类别的概率,并且归一为0-1范围易与非0即1的标签衡量误差。
交叉熵误差
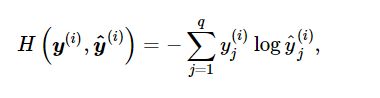
y(i)就是我们的标签,标签是非0即1的元素[1,0,1]。所以由公式可以得知,交叉熵误差函数只关心图片里存在的标签。如果每个图片只由一个存在则可以简化为H = -log*(该样本标签对应的预测值),比较简单。

动手学:多层感知机
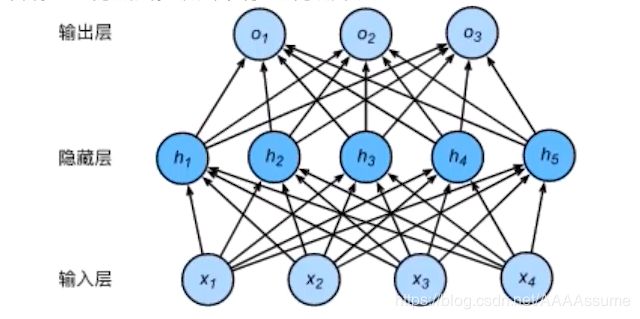
前面的神经网络都只有两层,输入层和输出层。深度学习探究的是大于2层以上的多层感知机,有一开始的输入层,结尾的输出层,中间的都叫隐藏层。两层之间的基础计算就是线性变换,和前面的计算没区别。
h1 = x1 * w11 + x2 * w21 + x3 * w31 + x4 * w41 + b1,
h2 = x1 * w12 + x2 * w22 + x3 * w32 + x4 * w42 + b2其他类推
第二层的计算也是一样,把隐藏层当作输入层,所以
o1 = h1 * w11 + h2 * w21 + h3 * w31 + h4 * w41 + h5 * w51 + b1,
o2 = h1 * w12 + h2 * w22 + h3 * w32 + h4 * w42 + h5 * w52 + b2,
这里的w和b和第一层的w和b是独立开来的,不是同一个,第一层就是第一层第二层就是第二层。每一条线都是权重,所以第一层权重有5 * 4+5(b)个,第二层有3 * 5+3个。由此可见两层之间就是简单的线性方程,即使加再多的隐藏层最多也只是线性变换的叠加,难以学习非线性关系,意义不大。
激活函数
为了解决这个问题,能让网络更好的学习到非线性关系,我们对隐藏层做一个非线性函数的变换再输出到下一层,这些非线性函数就是激活函数。常用的激活函数有ReLU函数,sigmoid函数,tanh函数。
ReLU(x) = max(x, 0)
sigmoid(x) = 1 / 1 + exp(-x)
tanh(x) = (1 - exp(-2x)) / (1 + exp(-2x))

文本预处理学习笔记()
文本就是词或者字符的序列,文本预处理有几个步骤
1.读入文本
2.分词
3.制作字典,每个词都映射到一个索引
4.把文本序列转换为索引序列,输入模型。因为计算机无法直接识别文本,所以要转换为词向量输入。
语言模型学习笔记()
语言模型就是一组词同时出现的概率,比如我_东西,通过训练的语言模型就可以得出填空里面是"拿"的概率比较大,填空里面是"海草"的概率很小。
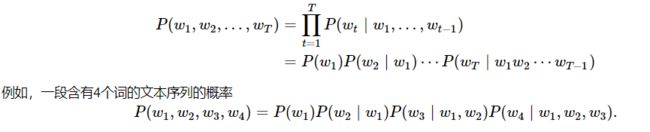
上面是语言模型的公式,P(w1) = n(w1) / n, P(w1|w2) = n(w1, w2) / n(w1)。n(w1)是指文本以w1作为第一个词的文本,n是指文本的数量。
n元语法
n元语法是上面的语言模型公式通过马尔可夫假设简化后的得到的语言模型方法。马尔可夫假设每个词只与前面的n个词有关系,而上面原始的是每个词与前面的全部词有关系。假设n = 2,
所以P(w1, w2, w3, w4) = P(w1)P(w2 | w1)P(w3 | w1,w2)P(w4 | w1,w2,w3)
就可以简化成P(w1, w2, w3, w4) = P(w1)P(w2 | w1)P(w3 | w1, w2)P(w4 | w2, w3)。
循环神经网络学习笔记()
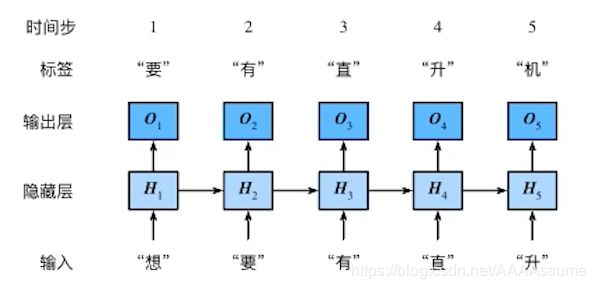
循环神经网络的不同处在于隐藏层Ht的计算,每个Ht的计算都依赖当前t的输入和前一个t的H,这样做可以考虑到前面的历史信息,因为文本后面的词都可能与前面的有关。并且这里的参数w和b只有一批,是一个网络循环使用,比如"想“用完就到"要","有"接着后面用。
![]()