阅读Disentangling and Unifying Graph Convolutions for Skeleton-Based Action Recognition(CVPR2020)

Disentangling and Unifying Graph Convolutions for Skeleton-Based Action Recognition(CVPR2020)
paper:https://arxiv.org/abs/2003.14111
code:github.com/kenziyuliu/ms-g3d

Abstract

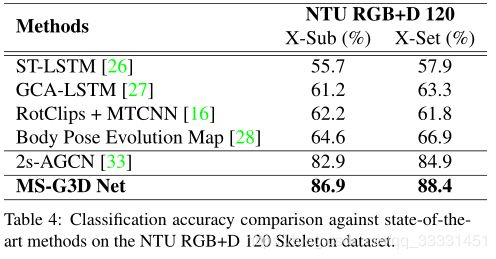
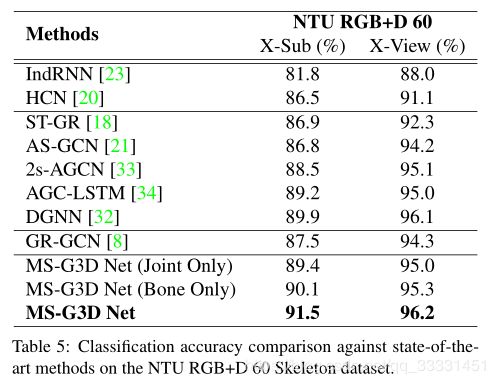
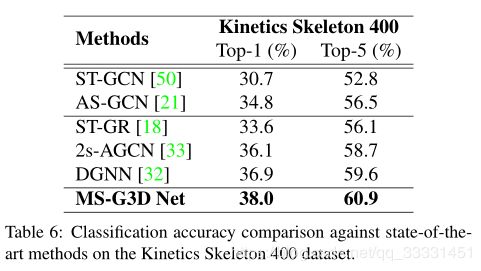
  基于骨架的动作识别算法中，时空图表示已广泛的应用于人体行为动力学的建模。为了从这些图表示中获得鲁棒性较好的模型，长距离、多尺度的上下文聚合和时空依赖建模是powerful特征提取的关键。然而，现有的方法在实现上存在局限性(1)多尺度算子下的无偏长距离联合关系建模(现有方法对邻域多采用多次求解来获取k阶邻接矩阵，这样会造成距离远近和重要程度成正相关，也就是有偏长距离关系建模)(2)无障碍跨时空信息流捕获复杂时空依赖(现有方法是时空交替训练，这样可以有效的使时空长距离建模，但阻碍了跨时空信息流直接交互，无法捕捉复杂区域时空节点关系)。根据上述问题，论文中作者提出了(1)分离多尺度图卷积的一种简单方法(2)统一的时空图卷积算子G3D，所提出的多尺度聚合方案将不同邻域中节点的重要性分离开来，以便进行有效的长距离建模。提出的G3D模块利用稠密的跨时空边作为跳跃连接，便于在时空图上直接传播信息。通过将这些方法结合起来，作者开发了一个功能强大的特征提取程序MS-G3D，在此基础上，作者的模型在三个大规模数据集（NTU RGB+d60、NTU RGB+d120和动力学骨架400）上优于以往的最优方法。

Introduction(摘)

  对于骨架的鲁棒动作识别，理想的算法应该超越局部关节的连通性，提取多尺度的结构特征和长距离相关性，因为结构上不相连关节也可能具有很强的相关性。现有方法通过骨架邻接矩阵的高阶多项式进行图卷积实现，幂级数表示节点的距离。虽然可以增加图卷积的感受野，但是公式存在有偏问题，较近的关节点总是比较远的关节点权重高。这意味着更高的多项式阶数在远距离关节特征捕捉时效果有限。
  鲁棒的算法能够利用复杂的跨时空联合关系进行动作识别，所以现有方法都是通过交叉部署时空模块，图卷积提取空间信息，采用1D Conv进行时间卷积。虽然这种方法可以捕捉长期的时间建模，但是它阻碍了跨时空的信息流交互。
  作者从两个方面来解决上述问题：

1. 提出了一种新的多尺度聚合方法，通过消除相邻邻域之间的冗余依赖解决有偏加权问题，从而在多尺度聚合下分离出它们的特征。
2. 提出了一种新的统一时空图卷积模块G3D，可以直接对跨时空的联合依赖建模。
   
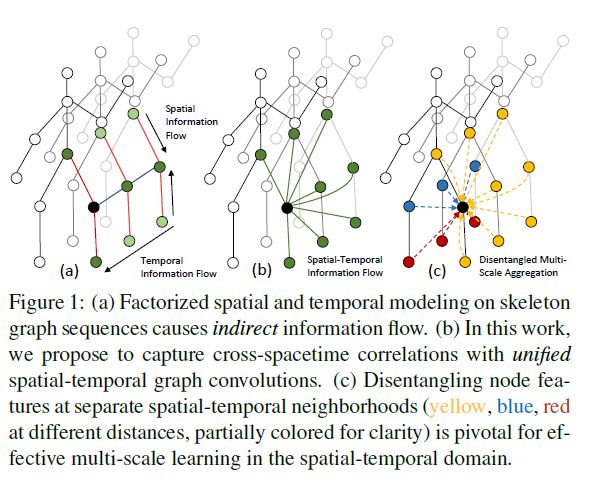
   G3D通过在“3D”时空域中引入图形边缘作为无障碍信息流的跳跃连接(图1(b))，实质上促进了时空特征学习。值得注意的是，尽管引入了额外的边，作者提出的分离聚合方案在时空中使用多尺度推理来增强G3D(图1©)，而不受有偏加权问题的影响。由此产生的强大的特征提取方法，名为MSG3D，构成了作者最终模型体系结构的一个构建块，在三个数据集上都优于最先进的方法。
   （i） 提出了一种分离的多尺度聚合方案，消除了不同邻域节点特征之间的冗余依赖，使得强大的多尺度聚合器能够有效地捕捉人体骨骼上的图关节关系。
   （ii）提出了一个统一的时空图卷积（G3D）算子，该算子有助于信息在时空间的直接流动，从而有效地进行特征学习。
   （iii）将分离聚合方案与G3D相结合，给出了一个功能强大的特征抽取器（MS-G3D），它具有跨时空维度的多尺度感受野。时空特征的直接多尺度聚合进一步提高了模型的性能。

Related Work

  G3D相比于GR-GCN，可以从多时间上下文学习，从多窗口和跳跃学习，更加具有普适性。

MS-G3D

3.2 Disentangled Multi-Scale Aggregation

Biased Weighting Problem. 现有方法都是通过高阶多项式来聚合时间t的多尺度结构信息$$X_t^{(l+1)}=\sigma (\sum _{k=0}^K{\hat{A}}^k{X}_t^{(l)}{\theta }_{(k)}^{(l)})\text{\hspace{1em}(2)}$$作者分析由于循环游走，距离较近的节点的k步可能比实际的k跳邻居的要多得多，这会导致对局部区域以及具有更高阶数的节点的偏移。GCN中的节点自循环允许更多可能的循环（因为游走总是可以在自循环），从而放大偏差。图示见图2。在骨架图的多尺度聚合下，聚合的特征将被局部身体部位信息支配，这使得获取具有更高多项式阶的长程联合依赖变得无效。如图2所示，如果按照之前的方法，k阶多项式的方法会出现高阶的信息“稀释”，低阶节点参数反而更大。

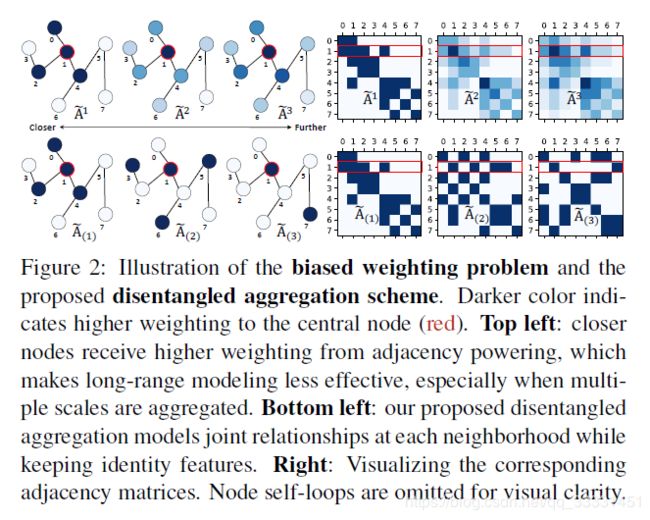
  提出了加权方案并对有偏问题进行了说明。颜色越深，表示中心节点的权重越大（红色）。左上：距离较近的节点从邻接能量中获得更高的权重，这使得远程建模的有效性降低，尤其是当多个尺度被聚合时。左下：我们提出的分离聚合模型在保持身份特征的同时，在每个邻域建立联合关系。右：显示相应的邻接矩阵。为了视觉清晰，省略了节点自循环。
Disentangling Neighborhoods. 作者定义的k阶邻接矩阵定义为：
$$[{\hat{A}}_{(k)}{]}_{i,j}=\{\begin{array}{rlrl}1& & \mathrm{i}\mathrm{f}& d(v_i,v_j)=k\\ 1& & \mathrm{i}\mathrm{f}& i=j\\ 0& & \mathrm{i}\mathrm{f}& otherwise\end{array}\text{\hspace{1em}(3)}$$
使用做差求解高阶邻接矩阵${\tilde{\mathrm{A}}}_{(\mathrm{k})}=\mathrm{I}+\mathbb{I}({\tilde{\mathrm{A}}}^{\mathrm{k}}\ge 1)-\mathbb{I}({\tilde{\mathrm{A}}}^{\mathrm{k}-1}\ge 1)$,最后得到的图卷积方程如下:
$$X_t^{(l+1)}=\sigma (\sum _{k=0}^K{\tilde{\mathrm{D}}}_{(\mathrm{k})}^{-\frac{1}{2}}{\tilde{\mathrm{A}}}_{(\mathrm{k})}{\tilde{\mathrm{D}}}_{(\mathrm{k})}^{-\frac{1}{2}}{\mathrm{X}}_{\mathrm{t}}^{(\mathrm{l})}{\mathrm{\Theta }}_{(\mathrm{k})}^{(\mathrm{l})})\text{\hspace{1em}(4)}$$
  与前面的情况不同，可能的长度k游走主要取决于长度k−1的游走，公式4中提出的分离公式通过消除远程邻域对近邻权重的冗余依赖来解决有偏权重问题。因此，在多尺度算子下，具有较大k的附加尺度以相加的方式聚合，使得具有较大k值的远距离建模保持有效。由此得到的k-邻接矩阵也比它们的高阶指数幂对应矩阵更稀疏（见图2），允许更有效的表示。

G3D: Unified Spatial-Temporal Modeling

  大多数现有的工作将骨架动作视为一系列分解图，其中特征是通过空间(例如gcn)和时间(例如TCNs)模块提取的。作者认为这样的“因子化公式”对于捕捉复杂的时空联合关系是不太有效的。显然，如果一对节点之间存在强连接，那么在分层传播过程中，该对节点应包含彼此的显著特征部分，以反映这种连接。然而，当信号通过一系列本地聚合器（gcn和tcn一样）跨时空传播时，当冗余信息从一个越来越大的时空感受野聚集时，它们会被削弱。如果观察到gcn没有执行加权聚合来区分每个邻居，那么问题就更明显了。
Cross-Spacetime Skip Connections. 为了解决上述问题，提出了一种更合理的方法来允许跨时空跳跃连接，这种连接很容易在时空图中用跨时空边进行建模。首先考虑输入图序列上$\tau$大小的滑动时间窗口，它在每一步都得到一个时空子图${\mathcal{G}}_{(\tau )}=({\mathcal{V}}_{(\tau )},{\epsilon }_{(\tau )})$,式中${\mathcal{V}}_{(\tau )}={\mathcal{V}}_{(1)}\cup ...\cup {\mathcal{V}}_{(\tau )}$是窗口中$\tau$帧上所有节点的并集。边集${\epsilon }_{(\tau )}$通过新的邻接矩阵$\tilde{A}$邻接矩阵块${\tilde{A}}_{(\tau )}$表示,其中：$${\tilde{A}}_{(\tau )}=\begin{array}{c}\left[\begin{array}{ccc}\tilde{A}& \dots & \tilde{A}\\ ⋮& \ddots & ⋮\\ \tilde{A}& \dots & \tilde{A}\end{array}\right]\in {\mathbb{R}}^{\tau N\tau N}\end{array}\text{\hspace{1em}(5)}$$每个邻接矩阵都是NxN的，每行每列都有$\tau$个，所以是$\tau N\times \tau N$,所以得到了3D特征模型：$$[{\mathrm{X}}_{(\tau )}^{(\mathrm{l}+1)}{]}_{\mathrm{t}}=\sigma ({\tilde{\mathrm{D}}}_{(\tau )}^{-\frac{1}{2}}{\tilde{\mathrm{A}}}_{(\tau )}{\tilde{\mathrm{D}}}_{(\tau )}^{-\frac{1}{2}}[{\mathrm{X}}_{(\tau )}^{(\mathrm{l})}{]}_{\mathrm{t}}{\mathrm{\Theta }}^{(\mathrm{l})})\text{\hspace{1em}(6)}$$其中，${\mathrm{X}}_{(\tau )}\in {\mathbb{R}}^{\mathrm{T}\times \tau \mathrm{N}\times \mathrm{C}}$
Dilated Windows. 上述加窗口结构的另一个重要方面是帧不必相邻。每d帧选取一帧，重复使用相同的时空结构${\tilde{A}}_{\tau }$，构造出具有$\tau$帧和膨胀率为d的扩展窗口。重复使用相同的时空结构${\tilde{A}}_{(\tau )}$。同样，我们可以得到节点特征${\mathrm{X}}_{\tau ,\mathrm{d}}\in {\mathbb{R}}^{\mathrm{T}\times \tau \mathrm{N}\times \mathrm{C}}$(如果省略，d=1)扩大的窗口允许更大的时间感受野，而不增加${\tilde{A}}_{\tau }$的大小，类似于扩张的卷积如何保持恒定的复杂性

Multi-Scale G3D. 我们也可以将所提出的分离多尺度聚合方案（式4）整合到G3D中，直接在时空域进行多尺度推理。因此，我们从等式6推导出MS-G3D模块为：$$[{\mathrm{X}}_{(\tau )}^{(\mathrm{l}+1)}{]}_{\mathrm{t}}=\sigma (\sum _{\mathrm{k}=0}^{\mathrm{K}}{\tilde{\mathrm{D}}}_{(\tau ,\mathrm{k})}^{-\frac{1}{2}}{\tilde{\mathrm{A}}}_{(\tau ,\mathrm{k})}{\tilde{\mathrm{D}}}_{(\tau ,\mathrm{k})}^{-\frac{1}{2}}[{\mathrm{X}}_{(\tau )}^{(\mathrm{l})}{]}_{\mathrm{t}}{\mathrm{\Theta }}_{(\mathrm{k})}^{(\mathrm{l})})\text{\hspace{1em}(7)}$$值得注意的是，作者提出的分解聚合方案补充了这个统一的算子，因为G3D从时空连通性增加的节点度可以导致有偏加权问题。
Discussion. 下面我们对G3D进行了更深入的分析。（1） 它类似于经典的三维卷积块，其时空感受野由$\tau$,$d$和$\tilde{A}$定义。（2）与三维卷积不同，G3D的参数计数来自${\Theta }_{(\cdot )}^{(\cdot )}$独立于$\tau$或$|{\epsilon }_{(\tau )}|$，因此通常不太容易过度拟合大$\tau$。（3） G3D中密集的跨时空连接需要在$\tau$上进行折衷，因为$\tau$的值越大，则时间感受场越大，而邻近区域越大，则会以更一般的特征为代价。此外，较大的$\tau$意味着二次方较大的${\tilde{A}}_{(\tau )}$，因此具有更多的多尺度聚集操作。另一方面，更大的扩展带来了更大的时间覆盖率，但代价是时间分辨率（较低的帧速率）。因此，$\tau$和$d$必须仔细平衡。（4） G3D模块被设计成捕捉复杂的区域时空关系，而不是通过因子分解模块更经济地捕获的长期相关性。因此，我们观察到当G3D模块被长程、因子化模块扩充时的最佳性能，这将在下一节中讨论。

3.4. Model Architecture

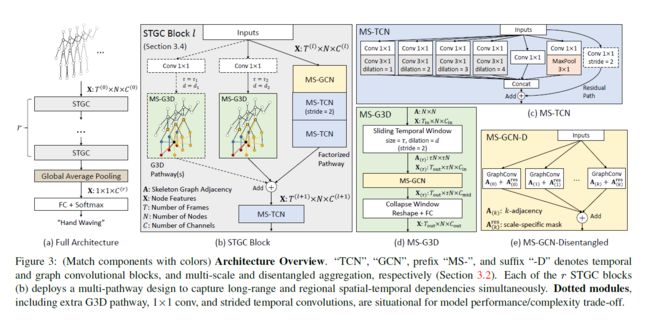
Overall Architecture. 最终的模型架构如图3所示。在较高的层次上，它包含一系列r个时空图卷积（STGC）块，从骨架序列中提取特征，然后是全局平均池层化和softmax分类器。每个STGC块都部署了两种类型的路径来同时捕获复杂的区域时空联合关联以及长期的时空依赖性：（1）G3D路径首先构造时空窗，对其进行分解多尺度图卷积，然后用一个完全连接的层将它们折叠起来，以便读取窗口特征。图3（b）所示的额外虚线G3D路径表明，该模型可以同时从具有不同$\tau$和$d$的多个时空上下文中学习；（2） 因子化路径通过长距离、仅空间和仅时间的模块扩充了G3D路径：第一层是多尺度的图卷积层，能够用最大K来建模整个骨架图；接着是两个多尺度时间卷积层，以捕获扩展的时间上下文（下面讨论）。所有路径的输出被聚合为STGC块输出，在典型的r=3块结构中，STGC块输出分别具有96、192和384个特征信道。批处理规范化和ReLU在除最后一层之外的每层末尾添加。除第一个外，所有STGC块降采样时间维度都使用stride 为2时间转换和滑动窗口。
Multi-Scale Temporal Modeling. G3D所使用的时空窗${\mathcal{G}}_{(}\tau )$本身是一个封闭的结构，这意味着G3D必须伴随时间模块进行跨窗口信息交换。许多现有的工作在整个体系结构中使用固定内核大小$k_t\times 1$的时间卷积来执行时间建模。作为多尺度空间聚集的自然延伸，我们通过多尺度学习增强了普通的时间卷积层，如图3（c）所示。为了降低额外分支所带来的计算成本，我们采用了bottleneck设计，将核大小固定为3×1，并使用不同的膨胀率，而不是更大的核来获得更大的感受野。我们还利用残差连接来促进训练。
Adaptive Graphs. 为了提高执行齐次邻域平均的图卷积层的灵活性，我们在每个${\tilde{A}}_{(k)}$和${\tilde{A}}_{(\tau ,k)}$上添加一个简单的可学习、无约束的图残差掩模，以动态地增强、减弱、添加或删除边。例如，公式4更新为:$${\mathrm{X}}_{(\mathrm{t})}^{(\mathrm{l}+1)}=\sigma (\sum _{\mathrm{k}=0}^{\mathrm{K}}{\tilde{\mathrm{D}}}_{(\mathrm{k})}^{-\frac{1}{2}}({\tilde{\mathrm{A}}}_{(\mathrm{k})}+{\mathrm{A}}_{(\mathrm{k})}^{\mathrm{r}\mathrm{e}\mathrm{s}}){\tilde{\mathrm{D}}}_{(\mathrm{k})}^{-\frac{1}{2}}{\mathrm{X}}_{\mathrm{t}}^{(\mathrm{l})}{\mathrm{\Theta }}_{(\mathrm{k})}^{(\mathrm{l})})\text{\hspace{1em}(8)}$$ $A^{res}$被初始化为0左右的随机值，并且对于每个k和τ都是不同的，允许每个多尺度上下文（空间或时空）选择最适合的掩码。还要注意的是，由于$A^{res}$针对所有可能的动作进行了优化，这些动作可能具有不同的特征传播的最佳边集，因此，当图结构存在重大缺陷时，它可能会给出较小的边校正，并且可能不够。特别是，$A^{res}$仅部分缓解了有偏权重问题（见第4.3节）。

Joint-Bone Two-Stream Fusion. 受到多篇文献中的双流方法的启发，以及可视化骨骼和关节可以帮助人类识别骨骼动作的直觉，我们使用了一个双流框架，其中使用初始化为远离身体的相邻关节向量差异的骨骼特征训练具有相同结构的单独模型居中。将来自关节/骨骼模型的softmax分数相加，以获得最终预测分数。由于骨架图是树，我们在身体中心添加一个零骨骼向量，从N个关节中获取N个骨骼，并重用A进行连接定义。

Experiments