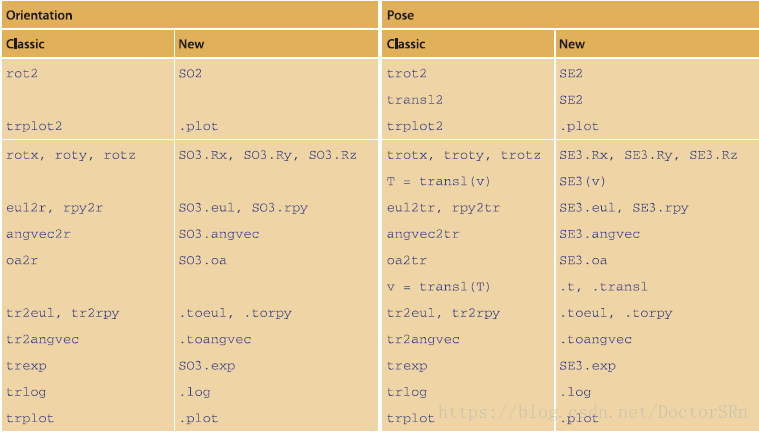
Robotics, Vision and Control, Second Edition读书笔记
Reading Note
Book: Robotics, Vision and Control, Second Edition
Author: Peter Corke
公开课: The open online robotics education resource
个人主页:www.doctorsrn.cn
摘录
- Robots are data-driven machines. They acquire data,
process it and take action based on it.- instant gratification: 及时行乐
- Robot definition: a goal oriented machine that can sense, plan and act.
- Further Reading: The Handbook of Robotics (Siciliano and Khatib 2016)
一个非常重要的问题:Matlab Robotics Toolbox中函数的参数涉及角度时使用的单位默认是弧度rad,但是在使用时发现实际情况是度deg,该问题的主要原因是调用的函数可能与MATLAB自带工具箱Phased Array System Toolbox中的函数重名导致的,比如rotx函数。所以可将该工具箱卸载来解决该问题。该问题可以参考Matlab Robotics Toolbox的官网,其中有介绍“Toolbox is using degrees not radians”问题。
2.1 Working in Two Dimensions (2D)
2.1.1 Orientation in 2-Dimensions
2.1.1.1 Orthonormal Rotation Matrix 正交旋转矩阵
Y坐标系相对于X坐标系的正交旋转矩阵为:
X R Y ( θ ) = ( c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ) ^{X}R_{Y}(\theta) = \begin{pmatrix} cos(\theta)& -sin(\theta)\\ sin(\theta)& cos(\theta) \end{pmatrix} XRY(θ)=(cos(θ)sin(θ)−sin(θ)cos(θ))
2.1.1.2 Matrix Exponential 矩阵指数
矩阵指数存在的性质:
R = rot2( θ \theta θ) 正交旋转矩阵
S = logm®
R = expm(S) 矩阵指数
S = skew( θ \theta θ)
θ \theta θ = vex(S)
2.1.2 Pose in 2-Dimensions
2.1.2.1 Homogeneous Transformation Matrix 齐次变换矩阵
从B坐标系到A坐标系的变换:
( A x A y 1 ) = ( A R B t 0 1 × 2 1 ) ( B x B y 1 ) \begin{pmatrix} ^{A}x& \\ ^{A}y& \\ 1& \end{pmatrix} = \begin{pmatrix} ^{A}R_{B}& t\\ 0_{1\times2}& 1 \end{pmatrix} \begin{pmatrix} ^{B}x& \\ ^{B}y& \\ 1& \end{pmatrix} ⎝⎛AxAy1⎠⎞=(ARB01×2t1)⎝⎛BxBy1⎠⎞
其中t=(x,y)。
引入齐次坐标,则上述变换可写为:
A p ~ = ( A R B t 0 1 × 2 1 ) B p ~ = A T B B p ~ ^{A}\tilde{p} = \begin{pmatrix} ^{A}R_{B}& t\\ 0_{1\times2}& 1 \end{pmatrix} \, ^{B}\tilde{p} = \, ^{A}T_{B}\,^{B}\tilde{p} Ap~=(ARB01×2t1)Bp~=ATBBp~
其中 A T B ^{A}T_{B} ATB是齐次变换矩阵。T的值为:
T = ( c o s ( θ ) − s i n ( θ ) x s i n ( θ ) c o s ( θ ) y 0 0 1 ) T = \begin{pmatrix} cos(\theta)& -sin(\theta)& x\\ sin(\theta)& cos(\theta)& y \\ 0& 0& 1 \end{pmatrix} T=⎝⎛cos(θ)sin(θ)0−sin(θ)cos(θ)0xy1⎠⎞
T的性质:
T − 1 = ( R t 0 1 × 2 1 ) − 1 = ( R T − R T t 0 1 × 2 1 ) T^{-1} = \begin{pmatrix} R& t\\ 0_{1\times2}& 1 \end{pmatrix}^{-1} = \begin{pmatrix} R^{T}& -R^{T}t\\ 0_{1\times2}& 1 \end{pmatrix} T−1=(R01×2t1)−1=(RT01×2−RTt1)
MATLAB相关命令:
T1 = transl2(1, 2) * trot2(30, 'deg')
plotvol([0 5 0 5]);
trplot2(T1, 'frame', '1', 'color', 'b')
T2 = transl2(2, 1)
T3 = T1*T2
trplot2(T2, 'frame', '2', 'color', 'r');
trplot2(T3, 'frame', '3', 'color', 'g');
T4 = T2*T1
trplot2(T4, 'frame', '4', 'color', 'c');
注意:T3和T4结果的差别说明,T1*T2表示,T2的变换是相对于T1坐标系进行的,所以3坐标系的原点不是(3,3),而4坐标系的原点是(3,3)。
另一个例子:
P=[3;2] %坐标(3,2)点
plot_point(P, 'label', 'P', 'solid', 'ko');
%求P点相对于坐标系1的坐标
P1 = inv(T1) * [P;1] %此处将P点写为齐次坐标的形式
%使用e2h函数也可实现普通点到齐次坐标的变化,h2e反之,即:
P1 = h2e(inv(T1) * e2h(P))
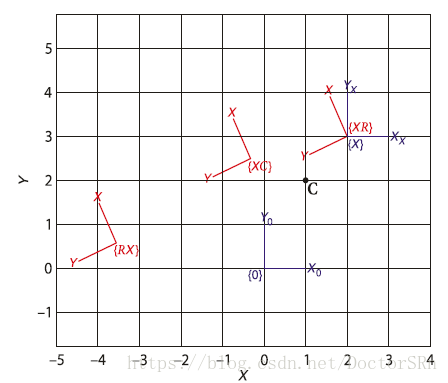
2.1.2.2 Centers of Rotation旋转中心
plotvol([-5 4 -1 5]);
T0 = eye(3,3);
trplot2(T0, 'frame', '0');
X = transl2(2, 3);
trplot2(X, 'frame', 'X');
R = trot2(2);
trplot2(R*X, 'framelabel', 'RX', 'color', 'r');
trplot2(X*R, 'framelabel', 'XR', 'color', 'r');
C = [1 2]';
plot_point(C, 'label', ' C', 'solid', 'ko')
RC = transl2(C) * R * transl2(-C)
trplot2(RC*X, 'framelabel', 'XC', 'color', 'r');
R*X: 旋转中心是原始坐标原点
X*R: 旋转中心是X坐标系原点
以任意点为旋转中心对X旋转变换:transl2© * R * transl2(-C) * X
2.1.2.3 Twists in 2D
- 使用Twist类型进行旋转变换
%创建以C点为旋转中心的Twist,C=[1 2]'
tw = Twist('R', C)
%获取以C点为旋转中心,旋转2 radians的变换矩阵
%该结果与上一节RC = transl2(C) * R * transl2(-C)得到的结果一样
T = tw.T(2)
%从Twist得到旋转中心
tw.pole()
- 使用Twist类型完成某方向上的平移变换
%沿(1,1)方向平移的Twist
tw = Twist('T', [1 1])
%平移√2
tw.T(sqrt(2))
- 更一般的变换
T = transl2(2, 3) * trot2(0.5)
%计算Twist向量值
tw = Twist(T)
%得到T
tw.T
#2.2 Working in Three Dimensions (3D)
Euler’s rotation theorem:
Any two independent orthonormal coordinate frames can be related by a sequence of rotations (not more than three) about coordinate axes, where no two successive rotations may be about the same axis.
2.2.1 Orientation in 3-Dimensions
2.2.1.1 Orthonormal Rotation Matrix
从B坐标系旋转至A坐标系:
( A x A y A z ) = A R B ( B x B y B z ) \begin{pmatrix} ^{A}x& \\ ^{A}y& \\ ^{A}z& \end{pmatrix} = \, ^{A}R_{B} \begin{pmatrix} ^{B}x& \\ ^{B}y& \\ ^{B}z& \end{pmatrix} ⎝⎛AxAyAz⎠⎞=ARB⎝⎛BxByBz⎠⎞
3维旋转矩阵的一些性质:
- 正交性,每列是单位向量,且列与列之间是正交的
- R − 1 = R T R^{-1} = R^{T} R−1=RT
- 正交旋转矩阵共9个元素,但是并不是彼此独立,各列是单位向量且彼此正交,提供6个约束条件,所以9个元素只有三个是独立的
各个轴的正交旋转矩阵:
R x ( θ ) = ( 1 0 0 0 c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) ) R_{x}(\theta) = \begin{pmatrix} 1& 0& 0\\ 0& cos(\theta)& -sin(\theta)\\ 0& sin(\theta)& cos(\theta) \end{pmatrix} Rx(θ)=⎝⎛1000cos(θ)sin(θ)0−sin(θ)cos(θ)⎠⎞
R y ( θ ) = ( c o s ( θ ) 0 s i n ( θ ) 0 1 0 − s i n ( θ ) 0 c o s ( θ ) ) R_{y}(\theta) = \begin{pmatrix} cos(\theta)& 0& sin(\theta)\\ 0& 1& 0\\ -sin(\theta)& 0& cos(\theta) \end{pmatrix} Ry(θ)=⎝⎛cos(θ)0−sin(θ)010sin(θ)0cos(θ)⎠⎞
R z ( θ ) = ( c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) 0 0 0 1 ) R_{z}(\theta) = \begin{pmatrix} cos(\theta)& -sin(\theta)& 0 \\ sin(\theta)& cos(\theta)& 0\\ 0& 0& 1 \end{pmatrix} Rz(θ)=⎝⎛cos(θ)sin(θ)0−sin(θ)cos(θ)0001⎠⎞
相关Matlab函数:
- rotx, roty, rotz (单位是deg)
- 可视化函数:trplot®, 动画tranimate®
2.2.1.2 Three- Angle Representations
根据Euler’s rotation theorem,有两类旋转方法:Eulerian and Cardanian
- Eulerian type: XYX, XZX, YXY, YZY, ZXZ, or ZYZ
- Cardanian type: XYZ, XZY, YZX, YXZ, ZXY, or ZYX
欧拉角
比如ZYZ序列: R = R z ( ϕ ) R y ( θ ) R z ( ψ ) R=R_{z}(\phi)R_{y}(\theta)R_{z}(\psi) R=Rz(ϕ)Ry(θ)Rz(ψ)
其对应的欧拉角为: Γ = ( ϕ , θ , ψ ) \Gamma=(\phi,\theta,\psi) Γ=(ϕ,θ,ψ)
例如欧拉角 Γ = ( 0.1 , 0.2 , 0.3 ) \Gamma=(0.1,0.2,0.3) Γ=(0.1,0.2,0.3),其对应的ZYZ旋转矩阵为:
R = rotz(0.1) * roty(0.2) * rotz(0.3);
%更便捷的求法
R = eul2r(0.1, 0.2, 0.3)
逆问题从旋转矩阵求欧拉角:
gamma = tr2eul(R)
注意:当 θ \theta θ角为负时,从旋转矩阵求出的欧拉角将和之前的值不一样, θ \theta θ将变为正值, ϕ , ψ \phi,\psi ϕ,ψ都将不同。这是因为从旋转矩阵到欧拉角的映射是不唯一的,且Matlab ToolBox中的函数总是返回正的 θ \theta θ角。
万向角
另一种常用的角度是Cardan angles(万向节角): roll, pitch and yaw.
常用序列为:ZYX or XYZ
- ZYX: R = R z ( θ y ) R y ( θ p ) R x ( θ r ) R=R_{z}(\theta_{y})R_{y}(\theta_{p})R_{x}(\theta_{r}) R=Rz(θy)Ry(θp)Rx(θr), 常用于船舶、汽车、航行器的姿态描述, X轴指向前进方向
- XYZ: R = R X ( θ y ) R y ( θ p ) R Z ( θ r ) R=R_{X}(\theta_{y})R_{y}(\theta_{p})R_{Z}(\theta_{r}) R=RX(θy)Ry(θp)RZ(θr),常用于机械臂末端执行器,Z轴指向前方,X轴指向上或者下
Matlab Toolbox默认ZYX序列,可使用’xyz’参数进行设置
R = rpy2r(0.1, 0.2, 0.3)
%逆操作
gamma = tr2rpy(R)
%xyz序列
R = rpy2r(0.1, 0.2, 0.3, 'xyz')
gamma = tr2rpy(R, 'xyz')
2.2.1.3 Singularities and Gimbal Lock 奇异点现象和万向节锁
当两个连续轴对齐时,欧拉角和万向节角的表示方法都会出现奇异点现象,即只能表示两个轴的姿态,第三个轴的姿态无法表示,出现自由度丢失的情况。对于ZYZ形式的欧拉角,当 θ = k π , k ∈ Z \theta = k\pi, k\in \mathbb{Z} θ=kπ,k∈Z时出现奇异点;对于万向节角,当pitch角 θ p = ± ( 2 k + 1 ) π 2 \theta_{p}=\pm(2k+1)\frac{\pi}{2} θp=±(2k+1)2π时出现奇异点。
2.2.1.4 Two Vector Representation双向量表示法
这种表示方法主要用于机械臂,考虑末端执行器坐标系为E,如下图
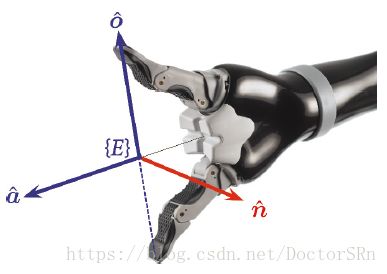
设工具指向的方向为Z轴,其对应的方向向量命名为approach vector(z向矢量),设为 a ^ = ( a x , a y , a z ) \hat{a}=(a_x,a_y,a_z) a^=(ax,ay,az)。设两指之间的指向为orientation vector(y向矢量), 设为 o ^ = ( o x , o y , o z ) \hat{o}=(o_x,o_y,o_z) o^=(ox,oy,oz)。使用 a ^ , o ^ \hat{a},\hat{o} a^,o^已经足够得到旋转矩阵R:
R = ( n x o x a x n y o y a y n z o z a z ) R = \begin{pmatrix} n_x& o_x& a_x \\ n_y& o_y& a_y\\ n_z& o_z& a_z \end{pmatrix} R=⎝⎛nxnynzoxoyozaxayaz⎠⎞
n ^ , o ^ , a ^ \hat{n},\hat{o},\hat{a} n^,o^,a^向量依次对应X,Y,Z轴。
- 当 a ^ , o ^ \hat{a},\hat{o} a^,o^正交时: n ^ = a ^ × o ^ \hat{n} = \hat{a}\times\hat{o} n^=a^×o^, n ^ \hat{n} n^称为normal vetor(x向矢量)。
Matlab对应指令:a = [1 0 0]'; o = [0 1 0]'; R = oa2r(o, a) - 当 a ^ , o ^ \hat{a},\hat{o} a^,o^不正交, a ^ , o ^ \hat{a},\hat{o} a^,o^也可以定义一个平面,并且可以计算出与该平面垂直的法向量 n ^ \hat{n} n^,然后可以得到与 a ^ , n ^ \hat{a},\hat{n} a^,n^正交的向量 o ^ ′ = a ^ × n ^ \hat{o}'=\hat{a}\times\hat{n} o^′=a^×n^
2.2.1.5 Rotation about an Arbitrary Vector绕任意向量旋转
任意朝向的两个坐标轴可以通过绕空间中某个轴旋转一次而重合。设旋转轴为向量v,旋转角为theta,Matlab实现:
R = rpy2r(0.1 , 0.2, 0.3);
[theta, v] = tr2angvec(R)
%求R的特征值和特征向量
[x,e] = eig(R)
%通过R的特征值求取旋转角
theta = angle(e(1,1))
v和theta不唯一。同时旋转矩阵R的特征值和特征向量存在如下关系:
因为特征值和特征向量存在关系: R v = λ v Rv={\lambda}v Rv=λv
当 λ = 1 \lambda=1 λ=1,即特征值为1时: R v = v Rv=v Rv=v
此时对应的特征向量v在旋转矩阵R的变换下不发生改变,即该特征向量就是旋转轴。一个正交旋转矩阵总有一个特征值 λ = 1 \lambda=1 λ=1,且另外两个特征值为共轭复数,满足 λ = c o s θ ± i s i n θ \lambda=cos\theta{\pm}isin\theta λ=cosθ±isinθ,此处 θ \theta θ就是旋转角。
逆问题:从旋转角和转轴向量求解旋转矩阵,使用Rodrigues旋转公式:
R = I 3 × 3 + s i n θ [ v ^ ] × + ( 1 − c o s θ ) [ v ^ ] × 2 R=I_{3\times3}+sin{\theta}[\hat{v}]_{\times}+ (1-cos\theta)[\hat{v}]^{2}_{\times} R=I3×3+sinθ[v^]×+(1−cosθ)[v^]×2
此处 [ v ^ ] × [\hat{v}]_{\times} [v^]×是偏斜对称矩阵。对应的Matlab实现为:
%绕X轴旋转pi/2的旋转矩阵
R = angvec2r(pi/2, [1 0 0])
2.2.1.6 Matrix Exponentials矩阵指数
R = rotx(0.3)
%求解矩阵对数
%结果是拥有两个元素的稀疏矩阵,大小为0.3
S = logm(R)
%S也是偏斜对称矩阵
%vex结果的第一个元素为旋转角0.3,对应于X轴为旋转轴
vex(S)'
%使用工具箱函数获取旋转角和旋转轴
[th,w] = trlog(R)
%矩阵对数函数logm的逆函数为矩阵指数函数expm
%重新得到旋转矩阵
expm(S)
%所以以下两个命令等价
R = rotx(0.3);
R = expm( skew([1 0 0]) * 0.3 );
绕任意轴旋转的情况可以写为:
R = e [ ω ] ^ × θ ∈ S O 3 R = e^{\hat{[\omega]}_\times\theta}\in{SO_3} R=e[ω]^×θ∈SO3
θ \theta θ是旋转角, ω ^ \hat{\omega} ω^是平行于旋转轴的单位向量,符号 [ ∙ ] × : R 3 ↦ R 3 × 3 [\bullet]_\times:\mathbb{R}^3\mapsto\mathbb{R}^{3\times3} [∙]×:R3↦R3×3表示从一个向量到偏斜对称矩阵的映射。
2.2.1.7 Unit Quaternions单位四元数
Quaternions定义:
q = s + v 1 i + v 2 j + v 3 k q=s+v_{\tiny1}i+v_{\tiny2}j+v_{\tiny3}k q=s+v1i+v2j+v3k
Unit Quaternions 满足:
∥ q ∥ = s 2 + v 1 2 + v 2 2 + v 3 2 = 1 \left \|q \right \| =s^2+v^2_{1}+v^2_{2}+v^2_{3} =1 ∥q∥=s2+v12+v22+v32=1
可以看做是绕单位向量 v ^ \hat{v} v^旋转 θ \theta θ角,满足关系式:
q ˚ = c o s θ 2 < v ^ s i n θ 2 > \mathring{q}=cos\frac{\theta}{2}<\hat{v}sin\frac{\theta}{2}> q˚=cos2θ<v^sin2θ>
对应的Matlab实现:
%注意角度单位是度还是弧度
q = UnitQuaternion( rpy2tr(0.1, 0.2, 0.3) )
inv(q)
q*inv(q)
q.R
q.plot()
%借助四元数进行旋转变换
q*[1 0 0]'
2.2.2 Pose in 3-Dimensions
2.2.2.1 Homogeneous Transformation Matrix
3维齐次变换矩阵与2维类似:
( A x A y A z 1 ) = ( A R B t 0 1 × 3 1 ) ( B x B y B z 1 ) \begin{pmatrix} ^{A}x& \\ ^{A}y& \\ ^{A}z& \\ 1& \end{pmatrix} = \begin{pmatrix} ^{A}R_{B}& t\\ 0_{1\times3}& 1 \end{pmatrix} \begin{pmatrix} ^{B}x& \\ ^{B}y& \\ ^{B}z& \\ 1& \end{pmatrix} ⎝⎜⎜⎛AxAyAz1⎠⎟⎟⎞=(ARB01×3t1)⎝⎜⎜⎛BxByBz1⎠⎟⎟⎞
引入齐次坐标,则上述变换可写为:
A p ~ = ( A R B t 0 1 × 3 1 ) B p ~ = A T B B p ~ ^{A}\tilde{p} = \begin{pmatrix} ^{A}R_{B}& t\\ 0_{1\times3}& 1 \end{pmatrix} \, ^{B}\tilde{p} = \, ^{A}T_{B}\,^{B}\tilde{p} Ap~=(ARB01×3t1)Bp~=ATBBp~
A T B ^{A}T_{B} ATB是4x4的齐次变换矩阵。
T的性质:
T 1 T 2 = ( R 1 t 1 0 1 × 3 1 ) ( R 2 t 2 0 1 × 3 1 ) = ( R 1 R 2 t 1 + R 1 t 2 0 1 × 3 1 ) T_1T_2 = \begin{pmatrix} R_1& t_1\\ 0_{1\times3}& 1 \end{pmatrix} \begin{pmatrix} R_2& t_2\\ 0_{1\times3}& 1 \end{pmatrix}= \begin{pmatrix} R_1R_2& t_1+R_1t_2\\ 0_{1\times3}& 1 \end{pmatrix} T1T2=(R101×3t11)(R201×3t21)=(R1R201×3t1+R1t21)
T − 1 = ( R t 0 1 × 3 1 ) − 1 = ( R T − R T t 0 1 × 3 1 ) T^{-1} = \begin{pmatrix} R& t\\ 0_{1\times3}& 1 \end{pmatrix}^{-1} = \begin{pmatrix} R^{T}& -R^{T}t\\ 0_{1\times3}& 1 \end{pmatrix} T−1=(R01×3t1)−1=(RT01×3−RTt1)
相关Matlab程序:
%注意角度单位问题
T = transl(1, 0, 0) * trotx(pi/2) * transl(0, 1, 0)
tranimate(T)
%旋转矩阵求解
t2r(T)
%坐标变换部分,一个列向量
transl(T)'
2.2.2.2 Vector-Quaternion Pair向量-四元数对
位姿的简洁、实用表示方法是向量-四元数对:
ξ ∼ ( t , q ˚ ) \xi \sim (t, \mathring{q}) ξ∼(t,q˚)
其中 t ∈ R 3 t \in \mathbb{R}^3 t∈R3是一个表征原坐标系与参考坐标系之间关系的向量, q ˚ ∈ S 3 \mathring{q} \in \mathbb{S}^3 q˚∈S3表征原坐标系相对于参考坐标系的朝向。
Note:这种方法Matlab Robotics Toolbox没有实现。
2.2.2.3 Twists
在三维空间,刚体的任意运动等效于螺旋运动–绕着空间中某条线旋转的同时沿着该线移动。
定义3维向量对Twist表征螺旋运动, s = ( v , ω ) ∈ R 6 s=(v,\omega) \in \mathbb{R}^6 s=(v,ω)∈R6。 ω \omega ω表征旋转轴, v v v表征twist轴在空间中的位置和螺旋运动的俯仰角。
Matlab相关代码:
%初始化一个单位twist,且转轴为x轴
tw = Twist('R', [1 0 0], [0 0 0])
%绕x轴旋转0.3rad,等价于trotx(0.3)
tw.T(0.3)
%创建沿y轴平移的twist
tw = Twist('T', [0 1 0])
%平移2个单位
tw.T(2)
一个关于螺旋运动模型的例子:
X = transl(3, 4, -4);
angles = [0:0.3:15];
%定义旋转轴
tw = Twist('R', [0 0 1], [2 3 2], 0.5);
%可视化
tranimate( @(theta) tw.T(theta) * X, angles, 'length', 0.5, 'retain', 'rgb', 'notext');
%获取旋转轴,并绘制出来
L = tw.line
L.plot('k:', 'LineWidth', 2)
将任意齐次变换转换为非单位twist:
T = transl(1, 2, 3) * eul2tr(0.3, 0.4, 0.5);
tw = Twist(T)
%俯仰角
tw.pitch
%关于轴的旋转
tw.theta
%旋转轴上的一点
tw.pole'
关于Twists的更多知识可参看该书籍和博客。
2.3 Advanced Topics
2.3.1 Normalization
矩阵或者四元数经过多次乘积运算会出翔精度丢失的问题,可以使用归一化的方法进行解决:
- 针对旋转矩阵:
trnorm(R) - 针对四元数:
q.unit()
2.3.2 Understanding the Exponential Mapping
本章讲解旋转矩阵(rotation matrices)、偏斜对称矩阵(skewsymmetric matrices)和矩阵指数(matrix exponentiation)之间的关系。
设一点P,其坐标向量为p,以角速度向量 ω \omega ω旋转, ω \omega ω的方向即为转轴方向。若使P点旋转 θ \theta θ角,则P点的线速度为:
p ˙ = ω × p \dot{p} = \omega \times p p˙=ω×p
将交叉积替换为偏斜对称矩阵和向量的积:
p ˙ = [ ω ] × p \dot{p} = [\omega]_\times p p˙=[ω]×p
对于上述方程的一阶形式(标量形式):
x ˙ = a x \dot{x} = ax x˙=ax
得一阶形式的解为:
x ( t ) = e a t x ( 0 ) x(t) = e^{at}x(0) x(t)=eatx(0)
原方程的解为:
p ( t ) = e [ ω ] × t p ( 0 ) p(t) = e^{[\omega]_{\times}t} p(0) p(t)=e[ω]×tp(0)
当 ∥ ω ∥ = 1 \left \| \omega \right \| = 1 ∥ω∥=1时,表示t秒之后旋转t rad。我们需要旋转 θ \theta θ角,所以设置 t = θ t = \theta t=θ,可得:
p ( θ ) = e [ ω ^ ] × θ p ( 0 ) p(\theta) = e^{[\hat{\omega}]_{\times}\theta} p(0) p(θ)=e[ω^]×θp(0)
该方程表示 p ( 0 ) p(0) p(0)被旋转至 p ( θ ) p(\theta) p(θ)。一个矩阵对向量进行旋转,该矩阵即是旋转矩阵:
R ( θ , ω ^ ) = e [ ω ^ ] × θ ∈ S O ( 3 ) R(\theta,\hat{\omega}) = e^{[\hat{\omega}]_{\times}\theta} \in \mathrm{SO(3)} R(θ,ω^)=e[ω^]×θ∈SO(3)
考虑一般情况下的旋转和平移运动:
p ˙ = [ ω ] × p + v \dot{p} = [\omega]_\times p + v p˙=[ω]×p+v
写为矩阵形式:
( p ˙ 0 ) = ( [ ω ] × v 0 0 ) ( p 1 ) \begin{pmatrix} \dot{p} \\ 0 \end{pmatrix} = \begin{pmatrix} [\omega]_\times& v\\ 0& 0 \end{pmatrix} \begin{pmatrix} p\\ 1 \end{pmatrix} (p˙0)=([ω]×0v0)(p1)
引入齐次坐标,上述方程写为:
p ~ ˙ = ( [ ω ] × v 0 0 ) p ~ = Σ p ~ \dot{\tilde{p}} = \begin{pmatrix} [\omega]_\times& v\\ 0& 0 \end{pmatrix} \tilde{p} =\Sigma \tilde{p} p~˙=([ω]×0v0)p~=Σp~
其中 Σ \Sigma Σ是4x4阶增广斜对称矩阵,可得其标量形式的解为:
p ~ ( θ ) = e Σ θ p ~ ( 0 ) \tilde{p}(\theta) = e^{\Sigma\theta}\tilde{p}(0) p~(θ)=eΣθp~(0)
可得齐次变换矩阵 T ( θ , ω ^ , v ) T(\theta,\hat\omega,v) T(θ,ω^,v)为:
T ( θ , ω ^ , v ) = e ( [ ω ^ ] × v 0 0 ) θ ∈ S E ( 3 ) T(\theta,\hat\omega,v) = e^{ \begin{pmatrix} [\hat\omega]_\times& v\\ 0& 0 \end{pmatrix} \theta } \in \mathrm{SE(3)} T(θ,ω^,v)=e([ω^]×0v0)θ∈SE(3)
以上讲解旋转矩阵(rotation matrices)、偏斜对称矩阵(skewsymmetric matrices)和矩阵指数(matrix exponentiation)之间的关系,Matlab实现的函数为expm和trexp。
2.3.4 Dual Quaternions对偶四元数
常规四元数只能表示空间旋转,而对偶四元数可以表示空间任意旋转和平移的组合。
2.3.5 Configuration Space构型空间
构型空间又称为C空间(C-Space),是系统所有可能的状态或配置(configuration)的集合,包括:
- 运动学:不考虑物理学时所有可能配置的几何形状
- 动力学:随时间推移,系统配置的演变
每个自由度就是C空间的其中一维,同时C空间张成的空间受到障碍物、关节限制等因素的约束。
配置(configuration)是系统参数的最小集合,且该集合可以描述系统上的任意一个点的位置,又被称为广义坐标。配置空间中的任意一个点可以映射到工作空间中的一个点,反之不一定为真。
工作空间的维度小于配置空间:系统过驱动(冗余),比如蛇形机器人
工作空间的维度大于配置空间:系统欠驱动
更多关于构型空间资料。
2.4 Using the Toolbox
Chapter 3 Time and Motion
3.1 Time-Varying Pose
3.1.1 Derivative of Pose
指数形势下位姿的导数:
表示坐标系朝向的方法有很多种,这里我们使用最方便的指数形式:
A R B ( t ) = e [ A ω ^ ( t ) ] × θ ( t ) ∈ S O ( 3 ) ^{A}\mathrm{R}_{B}(t) = e^{[^{A}\hat{\omega}(t)]_{\times}\theta(t)} \in \mathrm{SO(3)} ARB(t)=e[Aω^(t)]×θ(t)∈SO(3)
A ω ^ ( t ) ^{A}\hat{\omega}(t) Aω^(t)表示相对于A坐标系的旋转轴,转角为 θ ( t ) \theta(t) θ(t), [ ∙ ] × [\bullet]_{\times} [∙]×表示偏斜对称矩阵。
关于时间的导数:
A R ˙ B ( t ) = [ A ω ^ ( t ) ] × θ ˙ e [ A ω ^ ( t ) ] × θ ( t ) ∈ R 3 × 3 = [ A ω ^ ( t ) ] × θ ˙ A R B ( t ) ^{A}\dot{R}_{B}(t) = [^{A}\hat{\omega}(t)]_{\times} \dot{\theta} e^{[^{A}\hat{\omega}(t)]_{\times}\theta(t)} \in \mathbb{R^{3\times3}} =[^{A}\hat{\omega}(t)]_{\times}\dot{\theta} \, ^{A}\mathrm{R}_{B}(t) AR˙B(t)=[Aω^(t)]×θ˙e[Aω^(t)]×θ(t)∈R3×3=[Aω^(t)]×θ˙ARB(t)
令 A ω = A ω ^ θ ˙ ^A\omega= \, ^{A}\hat{\omega}\dot{\theta} Aω=Aω^θ˙,则 A ω ^A\omega Aω是相对于A坐标系的角速度,上述方程可重写为:
A R ˙ B = [ A ω ^ ] × A R B ∈ R 3 × 3 ^{A}\dot{R}_{B} = [^{A}\hat{\omega}]_\times \, ^{A}{R}_{B} \in \mathbb{R^{3\times3}} AR˙B=[Aω^]×ARB∈R3×3
B坐标系下的角速度变换至A坐标系:
A ω = A R B B ω ^A\omega = \, ^AR_B \, ^B\omega Aω=ARBBω
齐次变换矩阵形式下位姿的导数:
位姿的齐次矩阵形式:
ξ ∼ A T B = ( A R B A t B 0 1 × 3 1 ) \xi \sim\, ^AT_B = \begin{pmatrix} ^{A}R_{B}& ^At_B\\ 0_{1\times3}& 1 \end{pmatrix} ξ∼ATB=(ARB01×3AtB1)
其导数形式为:
ξ ˙ ∼ A T ˙ B = ( A R ˙ B A t ˙ B 0 1 × 3 0 ) = ( [ A ω ] × A R B A t ˙ B 0 1 × 3 0 ) \dot\xi \sim\, ^A\dot{T}_B = \begin{pmatrix} ^{A}\dot{R}_{B}& ^A\dot{t}_B\\ 0_{1\times3}& 0 \end{pmatrix} =\begin{pmatrix} [^{A}{\omega}]_\times \,^{A}{R}_{B}& ^A\dot{t}_B\\ 0_{1\times3}& 0 \end{pmatrix} ξ˙∼AT˙B=(AR˙B01×3At˙B0)=([Aω]×ARB01×3At˙B0)
B坐标系相对于A坐标系的平移速度即线速度为: v = A t ˙ B v=^A\dot{t}_{B} v=At˙B,B坐标系相对于A坐标系的角速度是 A ω B ^A{\omega}_B AωB。将上述两个速度向量组合为一个空间速度向量:
A v B = ( A v B , A ω B ) ∈ R 6 ^{\tiny{A}}v_{\tiny{B}} = (^{\tiny{A}}v_{\tiny{B}}, ^{\tiny{A}}\omega_{\tiny{B}}) \in \mathbb{R^6} AvB=(AvB,AωB)∈R6
这就是坐标系B相对于坐标系A的瞬时速度。
3.1.2 Transforming Spatial Velocities空间速度的变换
如下图,坐标系A是世界参考坐标系,坐标系B是运动物体坐标系:

空间速度 A v , B v , C v ^Av,\,^Bv,\,^Cv Av,Bv,Cv之间的变换关系为:
A v = ( A R B 0 3 × 3 0 3 × 3 A R B ) B v = A J B ( A ξ B ) B v ^Av = \begin{pmatrix} ^{A}R_{B}& 0_{3\times3}\\ 0_{3\times3}& ^{A}R_{B} \end{pmatrix} {^Bv} = {^A\mathit{J}_B}{(^A\xi_B)}{^Bv} Av=(ARB03×303×3ARB)Bv=AJB(AξB)Bv
C v = ( C R B [ C t B ] × C R B 0 3 × 3 C R B ) B v = A d ( C ξ B ) B v ^Cv = \begin{pmatrix} ^{C}R_{B}& [^Ct_B]_{\times}{^{C}R_{B}}\\ 0_{3\times3}& ^{C}R_{B} \end{pmatrix} {^Bv} = Ad{(^C\xi_B)}{^Bv} Cv=(CRB03×3[CtB]×CRBCRB)Bv=Ad(CξB)Bv
3.1.3 Incremental Rotation旋转的增量
占位?
3.1.4 Incremental Rigid-Body Motion 刚体运动的增量
占位?
3.2 Accelerating Bodies and Reference Frames
3.2.1 Dynamics of Moving Bodies动力学
占位?
3.2.2 Transforming Forces and Torques力和力矩的变换
占位?
wrench:力螺旋
3.2.3 Inertial Reference Frame惯性参考系
占位?
3.3 Creating Time-Varying Pose
- Path路径:空间曲线,从初始位姿到终时位姿
- Trajectory轨迹:指定时间参数的路径(运动时间、速度、加速度等),要求轨迹平滑
平滑:要求关于时间的前几阶导数是连续的,即要求速度、加速度、甚至加加速度是连续的。
3.3.1 Smooth One-Dimensional Trajectories
符合一维轨迹平滑要求的函数最常见的是多项式函数,比如五阶多项式函数:
s ( t ) = A t 5 + B t 4 + C t 3 + D t 2 + E t + F , t ∈ [ 0 , T ] s(t)=At^5+Bt^4+Ct^3+Dt^2+Et+F, \, t \in [0,T] s(t)=At5+Bt4+Ct3+Dt2+Et+F,t∈[0,T]
基于多项式函数的轨迹规划
- Matlab函数:
tpoly(),可指定初始时刻和终止时刻的参数 - 存在的问题:最大速度区域较少,没有充分利用电机的能力,会使机械臂的运动时间变长
混合轨迹的规划
为使最大速度的区域增大,可以使轨迹的某一段保持最大速度运动。
- Matlab函数:
lspb(),可指定最大速度 - 缺点:速度是平滑的,但是加速度不平滑
3.3.2 Multi-Dimensional Trajectories多维空间的轨迹规划
- Matlab函数:
mtraj(),使用示例:q = mtraj(@lspb, [0 2], [1 -1], 50)
3.3.3 Multi-Segment Trajectories多段轨迹
- Matlab函数:
mstraj(),生成多段多轴轨迹
3.3.4 Interpolation of Orientation in 3D
通过rpy角进行插值
%SO3.Rz输入参数的单位是度,而不是弧度
R0 = SO3.Rz(-10) * SO3.Ry(-10);
R1 = SO3.Rz(10) * SO3.Ry(10);
%.rpy的输出参数的单位是弧度
rpy0 = R0.torpy(); rpy1 = R1.torpy();
rpy = mtraj(@tpoly, rpy0, rpy1, 50);
rpy = rad2deg(rpy)
%SO3.rpy 输入参数rpy的默认单位是角度而不是弧度
SO3.rpy(rpy). animate;
通过单位四元数进行插值
使用spherical linear interpolation(球面线性插值)
q0 = R0. UnitQuaternion; q1 = R1.UnitQuaternion;
q = interp(q0, q1, 50);
q.animate
3.3.4.1 Direction of Rotation
不同方向的旋转即使都能到达目标点,但是角位移不一样。
Matlab程序:
%正常旋转,角位移较大
q0 = UnitQuaternion.Rz(-2); q1 = UnitQuaternion.Rz(2);
q = interp(q0, q1, 50);
q.animate()
%使用'shortest'参数,将选择最短路径
q = interp(q0, q1, 50, 'shortest');
q.animate()
3.3.5 Cartesian Motion in 3D
通常要求SE(3)空间中的位姿之间的路径平滑,即位置和方向的变化都要求平滑。
Matlab程序:
n = 180/pi;
T0 = SE3([0.4, 0.2, 0]) * SE3.rpy(0, 0, 3*n);
T1 = SE3([-0.4, -0.2, 0.3]) * SE3.rpy(-pi/4*n, pi/4*n, -pi/2*n);
Ts = interp(T0, T1, 50);
Ts.animate
%绘制位置坐标变换情况
P = Ts.transl;
plot(P);
%绘制方向坐标变化情况
rpy = Ts.torpy;
plot(rpy);

从运行结果可知,位置坐标的变化是平滑且线性的,方向坐标的变化是平滑的。但是在起点和终点的速度和加速度不是连续的。
interp函数:interp对两点之间的归一化路径进行插值,所以Ts = interp(T0, T1, 0.5)表示T0和T1之间路径的中点。
如果使用多项式插值或者多段插值的方法就可以克服速度和加速度不连续的问题,使用方法为:Ts = T0. interp(T1, lspb(0, 1, 50) ),或者直接使用笛卡尔轨迹规划函数:Ts = ctraj(T0, T1, 50)

Part III Arm-Type Robots
7.1 Forward Kinematics
从关节坐标系或者配置空间到末端执行器位姿的映射。
7.1.1 2-Dimensional (Planar) Robotic Arms
- 图a的变换公式:
ξ E ( q ) = R z ( q 1 ) ⊕ T x ( a 1 ) \xi_E(q) = \mathcal{R}_z(q_{\tiny{1}}) \oplus \mathcal{T}_x(a_{\tiny{1}}) ξE(q)=Rz(q1)⊕Tx(a1) - 图b的变换公式:
ξ E ( q ) = R z ( q 1 ) ⎵ j o i n t 1 ⊕ T x ( a 1 ) ⎵ l i n k 1 ⊕ R z ( q 2 ) ⎵ j o i n t 2 ⊕ T x ( a 2 ) ⎵ l i n k 2 \xi_E(q) = \underbrace{\mathcal{R}_z(q_{\tiny{1}}) }_{joint1} \oplus \underbrace{\mathcal{T}_x(a_{\tiny{1}})}_{link1} \oplus \underbrace{\mathcal{R}_z(q_{\tiny{2}}) }_{joint2} \oplus \underbrace{\mathcal{T}_x(a_{\tiny{2}})}_{link2} ξE(q)=joint1 Rz(q1)⊕link1 Tx(a1)⊕joint2 Rz(q2)⊕link2 Tx(a2)
对应的Matlab仿真程序:
这种两关节结构自由度为2,配置空间为: C = S 1 × S 1 \mathcal{C} = \mathbb{S}^1 \times \mathbb{S}^1 C=S1×S1,可以到达的工作空间为 T ⊂ R 2 \mathcal{T} \subset \mathbb{R}^2 T⊂R2,对于工作空间 T ⊂ S E ( 2 ) \mathcal{T} \subset \mathrm{SE}(2) T⊂SE(2)则无法完全到达。import ETS2.* a1 = 1; a2 = 1; E = Rz('q1') * Tx(a1) * Rz('q2') * Tx(a2) E.fkine( [30, 40], 'deg') E.plot( [30, 40], 'deg') E.teach %关节类型 %R:表示铰链结构 P:表示滑杆结构 %返回RR E.structure - 图c的变换公式:
ξ E ( q ) = R z ( q 1 ) ⎵ j o i n t 1 ⊕ T x ( a 1 ) ⎵ l i n k 1 ⊕ T x ( q 2 ) ⎵ j o i n t 2 \xi_E(q) = \underbrace{\mathcal{R}_z(q_{\tiny{1}}) }_{joint1} \oplus \underbrace{\mathcal{T}_x(a_{\tiny{1}})}_{link1} \oplus \underbrace{\mathcal{T}_x(q_{\tiny{2}}) }_{joint2} ξE(q)=joint1 Rz(q1)⊕link1 Tx(a1)⊕joint2 Tx(q2)
对应的Matlab仿真程序:import ETS2.* a1 = 1; E = Rz('q1') * Tx(a1) * Tx('q2') E.plot( [30, 40], 'deg') E.teach %关节类型 %R:表示铰链结构 P:表示滑杆结构 %返回RP E.structure - 三关节的平面机械臂变换公式:
ξ E ( q ) = R z ( q 1 ) ⎵ j o i n t 1 ⊕ T x ( a 1 ) ⎵ l i n k 1 ⊕ R z ( q 2 ) ⎵ j o i n t 2 ⊕ T x ( a 2 ) ⎵ l i n k 2 ⊕ R z ( q 3 ) ⎵ j o i n t 3 ⊕ T x ( a 3 ) ⎵ l i n k 3 \xi_E(q) = \underbrace{\mathcal{R}_z(q_{\tiny{1}}) }_{joint1} \oplus \underbrace{\mathcal{T}_x(a_{\tiny{1}})}_{link1} \oplus \underbrace{\mathcal{R}_z(q_{\tiny{2}}) }_{joint2} \oplus \underbrace{\mathcal{T}_x(a_{\tiny{2}})}_{link2} \oplus \underbrace{\mathcal{R}_z(q_{\tiny{3}}) }_{joint3} \oplus \underbrace{\mathcal{T}_x(a_{\tiny{3}})}_{link3} ξE(q)=joint1 Rz(q1)⊕link1 Tx(a1)⊕joint2 Rz(q2)⊕link2 Tx(a2)⊕joint3 Rz(q3)⊕link3 Tx(a3)
该结构的机械臂可以到达任务空间 T ⊂ S E ( 2 ) \mathcal{T} \subset \mathrm{SE}(2) T⊂SE(2)中的任何点。
7.1.2 3-Dimensional Robotic Arms
真正有用的机械臂它的工作空间应该是 T ⊂ S E ( 3 ) \mathcal{T} \subset \mathrm{SE}(3) T⊂SE(3),就是说机械臂末端执行器可以到达空间中的任意位置和姿态。

如上图,使用PUMA560机械臂模型作为仿真对象,MATLAB中调用该模型的方法如下:
%matlab 2018a
mdl_puma560
p560.teach
对应的正运动学的变换公式为:
ξ E ( q ) = T z ( L 1 ) ⊕ R z ( q 1 ) ⊕ R y ( q 2 ) ⊕ T y ( L 2 ) ⊕ T z ( L 3 ) ⊕ R y ( q 3 ) \xi_E(q) = \mathcal{T}_z(L_{\tiny{1}}) \oplus \mathcal{R}_z(q_{\tiny{1}}) \oplus \mathcal{R}_y(q_{\tiny{2}}) \oplus \mathcal{T}_y(L_{\tiny{2}}) \oplus \mathcal{T}_z(L_{\tiny{3}}) \oplus \mathcal{R}_y(q_{\tiny{3}}) ξE(q)=Tz(L1)⊕Rz(q1)⊕Ry(q2)⊕Ty(L2)⊕Tz(L3)⊕Ry(q3)
⊕ T x ( L 4 ) ⊕ T y ( L 5 ) ⊕ T z ( L 6 ) ⊕ R z ( q 4 ) ⊕ R y ( q 5 ) ⊕ R z ( q 6 ) ⎵ w r i s t \oplus \mathcal{T}_x(L_{\tiny{4}}) \oplus \mathcal{T}_y(L_{\tiny{5}}) \oplus \mathcal{T}_z(L_{\tiny{6}}) \oplus \underbrace{\mathcal{R}_z(q_{\tiny{4}}) \oplus \mathcal{R}_y(q_{\tiny{5}}) \oplus \mathcal{R}_z(q_{\tiny{6}}) }_{wrist} ⊕Tx(L4)⊕Ty(L5)⊕Tz(L6)⊕wrist Rz(q4)⊕Ry(q5)⊕Rz(q6)
最后的腕部(wrist)使用欧拉角的ZYZ变换顺序。
相关的Matlab程序:
import ETS3.*
L1 = 0; L2 = -0.2337; L3 = 0.4318; L4 = 0.0203; L5 = 0.0837; L6 = 0.4318;
E3 = Tz(L1) * Rz('q1') * Ry('q2') * Ty(L2) * Tz(L3) * Ry('q3')
* Tx(L4) * Ty(L5) * Tz(L6) * Rz('q4') * Ry('q5') * Rz('q6');
%正向运动学
E3.fkine([0 0 0 0 0 0])
7.1.2.1 Denavit-Hartenberg Parameters
假设一个机械臂有N个关节,标号为1到N,则其有N+1个连杆,可以标号为0到N。所以关节j连接着连杆j-1和连杆j,同时连杆l连接着关节l和关节l+1。通常连杆0是机械臂的底座,是固定的;连杆N是机械臂的末端执行器。
D-H参数法通过定义两个相邻关节坐标轴之间的空间关系来表示机械臂连杆的几何结构。并且D-H参数在定义时,机械臂必须处于一个特殊的配置–the zero-angle configuration(零位)。
同时要求坐标系{j}连接在连杆j的远端,坐标系{j}的z轴与j+1关节轴对齐。如下图所示:
D-H参数图示:
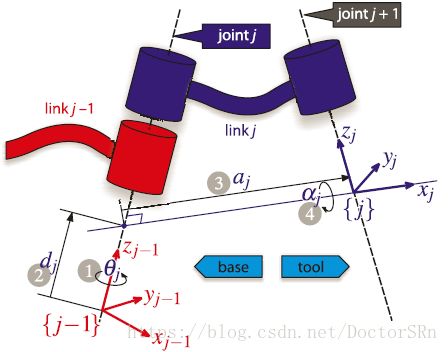
从连杆坐标系 {j-1}到坐标系{j}的变换为:
j − 1 ξ j ( θ j , d j , a j , α j ) = R z ( θ j ) ⊕ T z ( d j ) ⊕ T x ( a j ) ⊕ R x ( α j ) ^{j-1}\xi_j(\theta_j,d_j,a_j,\alpha_j)= \mathcal{R}_z(\theta_{\tiny{j}}) \oplus \mathcal{T}_z(d_{\tiny{j}}) \oplus \mathcal{T}_x(a_{\tiny{j}}) \oplus \mathcal{R}_x(\alpha_{\tiny{j}}) j−1ξj(θj,dj,aj,αj)=Rz(θj)⊕Tz(dj)⊕Tx(aj)⊕Rx(αj)
写为齐次矩阵形式:
j − 1 A j = ( c o s θ j − s i n θ j c o s α j s i n θ j s i n α j a j c o s θ j s i n θ j c o s θ j c o s α j − c o s θ j s i n α j α j s i n θ j 0 s i n α j c o s α j d j 0 0 0 1 ) ^{j-1}A_j = \begin{pmatrix} cos\theta_j& -sin\theta_jcos\alpha_j& sin\theta_jsin\alpha_j& a_jcos\theta_j\\ sin\theta_j& cos\theta_jcos\alpha_j& -cos\theta_jsin\alpha_j& \alpha_jsin\theta_j\\ 0& sin\alpha_j& cos\alpha_j& d_j\\ 0& 0& 0& 1 \end{pmatrix} j−1Aj=⎝⎜⎜⎛cosθjsinθj00−sinθjcosαjcosθjcosαjsinαj0sinθjsinαj−cosθjsinαjcosαj0ajcosθjαjsinθjdj1⎠⎟⎟⎞
Note:对于旋转关节(revolute joint), θ j \theta_j θj是随关节转动而变化的, d j d_j dj是常数;而对于平移型关节(prismatic joint), d j d_j dj是变化的, θ j \theta_j θj是固定不变的,且 α j = 0 \alpha_j = 0 αj=0。所以使用广义关节坐标系 q j q_j qj统一表示revolute joint情况下的 θ j \theta_j θj和prismatic joint情况下的 d j d_j dj。
对于N轴机械臂,广义关节坐标 q ∈ C q \in \mathcal{C} q∈C,此处的 C ∈ R N \mathcal{C} \in \mathbb{R}^N C∈RN就是关节空间或配置空间。
相关Matlab程序:
%创建一个revolution型关节
L = Revolute('a', 1)
%q=0.5 进行变换
L.A(0.5)
正向运动学是关节坐标的函数,简单来说就是由每个链接的相对姿势的决定的:
0 ξ N = K ( q ; θ , d , a , α , σ ) = 0 ξ 1 ⊕ 1 ξ 2 ⋯ N − 1 ξ N ^0\xi_N = \mathcal{K}(\mathbf{q};\theta,\mathbf{d},\mathbf{a},\alpha, \sigma) = {^0\xi_1} \oplus {^1\xi_2} \cdots {^{N-1}\xi_N} 0ξN=K(q;θ,d,a,α,σ)=0ξ1⊕1ξ2⋯N−1ξN
上述公式中连杆0表示机器人的底座,通常 d 1 = 0 d_1=0 d1=0。
相关Matlab程序:
%使用SerialLink搭建机械臂模型
robot = SerialLink( [ Revolute('a', 1) Revolute('a', 1) ], 'name', 'my robot')
%进行正运动学解算
robot.fkine([30 40], 'deg')
7.1.2.2 Product of Exponentials
使用指数积表示机械臂正运动学:
ξ E ∼ 0 T E = e [ S 1 ] q 1 ⋯ e [ S N ] q N 0 T E ( 0 ) \xi_E \sim {^0T_E} = e^{[S_1]q_1} \cdots e^{[S_N]q_N} {^0T_E(0)} ξE∼0TE=e[S1]q1⋯e[SN]qN0TE(0)
此处的 0 T E ( 0 ) {^0T_E(0)} 0TE(0)表示末端执行器在关节坐标全为0时的位姿。
7.1.2.3 6-Axis Industrial Robot
Puma560 6轴机器人模型的仿真示例:
mdl_puma560
%绘制机械臂处于零位(zero angle)的模型图
p560.plot(qz)
%零位时的正运动学运算
TE = p560.fkine(qz)
%设置末端工具的位姿
p560.tool = SE3(0, 0, 0.2);
%设置机械臂底座的参数,默认全为零
%puma560有一个30-inch高的基座
p560.base = SE3(0, 0, 30*0.0254);
%再次进行正运动学运算
p560.fkine(qz)
7.2 Inverse Kinematics
逆运动学:
q = K − 1 ( ξ ) \mathbf{q} = \mathcal{K}^{-1}(\xi) q=K−1(ξ)
可以使用两种方法来求解逆运动学:
- 封闭形式或解析解可以使用几何或代数方法确定。但随着关机数增多,封闭形式的解可能不存在。
- 迭代数值解
7.2.1 2-Dimensional (Planar) Robotic Arms
使用一个两关节的平面机械臂进行逆运动学原理的说明。
7.2.1.1 Closed-Form Solution
求解封闭解的Matlab程序:
import ETS2.*
a1 = 1; a2 = 1;
E = Rz('q1') * Tx(a1) * Rz('q2') * Tx(a2)
syms q1 q2 real
%正运动学求解
TE = E.fkine( [q1, q2] )
%定义末端执行器的位姿
syms x y real
%TE.t = (x,y)
%第一个方程。在符号工具箱中‘=’表示赋值
% ‘==’表示相等
e1 = x == TE.t(1)
%第二个方程
e2 = y == TE.t(2)
%求解方程组
%得到的解有两组
[s1,s2] = solve( [e1 e2], [q1 q2] )
7.2.1.2 Numerical Solution 数值解
可将逆运动学看成是优化问题–使正向运动学的解和目标位姿之间的误差最小化:
q ∗ = a r g m i n q ∥ K ( q ) ⊖ ξ ∗ ∥ \mathbf{q}^* = arg \mathop{min}\limits_{q} \left \| \mathcal{K}(\mathbf{q}) \ominus \xi^* \right \| q∗=argqmin∥K(q)⊖ξ∗∥
所以对于2连杆结构的平面机械臂,其误差函数为:
E ( q ) = ∥ [ K ( q ) ] t − ( x ∗ y ∗ ) T ∥ E(q) = \left \| [\mathcal{K}(\mathbf{q})]_t - (x^* \, y^*)^T \right \| E(q)=∥∥[K(q)]t−(x∗y∗)T∥∥
使用Matlab进行数值解求解:
%初始化目标位置
pstar = [0.6; 0.7];
%数值解,只得到一组解,而解析解有两组
%q的初始值决定了所得到的解析解
q = fminsearch( @(q) norm( E.fkine(q).t - pstar ), [0 0] )
%测试求解结果
E.fkine(q).print
7.2.2 3-Dimensional Robotic Arms
7.2.2.1 Closed-Form Solution
六轴机械臂封闭解存在的必要条件是它是球形腕部结构。使用PUMA560的D-H参数模型进行原理说明(PUMA560是球形腕部结构)。
Matlab程序:
mdl_puma560
%标称关节坐标nominal joint coordinates
qn
%正向运动学
T = p560.fkine(qn)
%使用ikine6s求解逆运动学的封闭解
%ikine6s函数会根据D-F判断是否满足封闭解的条件
qi = p560.ikine6s(T)
p560.fkine(qi)
%强制使用右手解模式,此时所得结果与qn一致
%ikine6s不同的求解模式:
%left or right handed 'l', 'r'
%elbow up or down 'u', 'd'
%wrist fl ipped or not fl ipped 'f', 'n'
qi = p560.ikine6s(T, 'ru')
%逆解不存在
p560.ikine6s( SE3(3, 0, 0) )
%q5=0出现奇异点现象
q = [0 pi/4 pi 0.1 0 0.2];
p560.ikine6s(p560.fkine(q), 'ru')
q(4)+q(6)
可以发现使用ikine6s函数求得的逆解和qn不一样,但是qi的正运动学结果和qn一致:
事实上有8组关节坐标其正运动学对应的末端执行器的位姿一致。但由于机械结构的限制和障碍物的存在,8组解并不是都能在物理上实现。同时也存在一些不可达位姿。
由于奇异点问题,有的位姿也是不可达的,因为轴的对齐使有效自由度减少(万向节锁定问题)。
对于PUMA560,当 q 5 = 0 q_5=0 q5=0,时关节4和6对齐。此时只要 q 4 + q 5 q_4+q_5 q4+q5的值不变,任意 q 4 q_4 q4、 q 5 q_5 q5的值对应的位姿一样。
7.2.2.2 Numerical Solution
对于非6关节和球形腕部结构的机械臂,可以使用迭代数值方法求解逆运动学解。Matlab中迭代数值求解函数为ikine。
Matlab程序:
%标称关节坐标nominal joint coordinates
qn
T = p560.fkine(qn)
qi = p560.ikine(T)
p560.fkine(qi)
p560.plot(qi)
%给定关节角初始值,默认全为0
qi = p560.ikine(T, 'q0', [0 0 3 0 0 0])
Note:数值法ikine比解析法ikine6s运行慢,但是在解决机械臂奇异点问题和机械臂关节角个数不为6的情况时有很大的优势。
7.2.2.3 Under-Actuated Manipulator欠驱动机械臂
关节数少于6的机械臂称为欠驱动机械臂,因为其末端执行器在空间中所能到达的位姿存在限制。通常情况下工作空间是 x − y − z − θ x-y-z-\theta x−y−z−θ,即 T ⊂ R 3 × S 1 \mathcal{T} \subset \mathbb{R}^3 \times \mathbb{S}^1 T⊂R3×S1,配置空间是 C ⊂ ( S 1 ) 3 × R \mathcal{C} \subset (\mathbb{S}^1)^3 \times \mathbb{R} C⊂(S1)3×R。
以SCARA Robot为例,这是一个RRPR型4轴机械臂:
mdl_cobra600
c600
%注意RPY的单位,我的MATLAB默认是deg
%书中程序是:
%T = SE3(0.4, -0.3, 0.2) * SE3.rpy(30, 40, 160, 'deg')
T = SE3(0.4, -0.3, 0.2) * SE3.rpy(30, 40, 160)
%逆运动学求解,忽略x、y轴的旋转
q = c600.ikine(T, 'mask', [1 1 1 0 0 1])
Ta = c600.fkine(q);
Ta.print('xyz')
trplot(T, 'color', 'b')
hold on
trplot(Ta, 'color', 'r')
由于该型机械臂末端执行器的姿态只能以z-轴为旋转轴进行旋转,所以目标位姿T是过约束的,T沿x和y轴的旋转是无效的,所以使用ikine数值法求逆解时,使用’mask’参数将沿x和y轴的旋转进行忽略。最终求得的关节角q对应的末端执行器的位姿是满足该机械臂物理约束的,即末端执行器坐标系的z轴是垂直的。
7.2.2.4 Redundant Manipulator冗余机械臂
关节数大于6的机械臂称为冗余机械臂。虽然理论上拥有6个关节的机械臂就可以到达笛卡尔工作空间的任意期望位姿,但实际上由于关节限制、奇异点等因素的存在,并不能完全实现到达任意位姿。所以添加更多的关节就是解决这个问题的一个办法,但是这又会导致关节坐标的解有无数个。为了解决关节坐标的解无数多的问题,需要引入约束条件,常用的约束是最小范数–返回的关节坐标向量解满足范数值最小。
以Baxter robot为例,该机器人有两个机械臂,且每个机械臂有7个关节。
mdl_baxter
%左臂
left
TE = SE3(0.8, 0.2, -0.2) * SE3.Ry(pi);
%此时ikine获得的逆解关节坐标向量q满足范数最小
q = left.ikine(TE)
left.fkine(q).print('xyz')
left.plot(q)
7.3 Trajectories
对于机械臂最普遍的需求是可以将末端执行器从一个位姿平滑的移动至另一个位姿。常用的生成轨迹的两种方法是:在配置空间(也即关节空间)直线移动,或者在任务空间(也即笛卡尔空间)直线移动。
7.3.1 Joint-Space Motion 关节空间的运动
Matlab仿真程序:
mdl_puma560
T1 = SE3(0.4, 0.2, 0) * SE3.Rx(pi);
T2 = SE3(0.4, -0.2, 0) * SE3.Rx(pi/2);
q1 = p560.ikine6s(T1);
q2 = p560.ikine6s(T2);
%50 ms步长,2s内移动到
t = [0:0.05:2]';
%借助mtraj函数生成轨迹
%使用tpoly插值
q = mtraj(@tpoly, q1, q2, t);
%使用lspb
q = mtraj(@lspb, q1, q2, t);
%或者使用将mtraj和tpoly封装的函数jtraj
%可获取速度和加速度:
%[q,qd,qdd] = jtraj(q1, q2, t);
q = jtraj(q1, q2, t);
%可使用类方法进行轨迹规划
q = p560.jtraj(T1, T2, t)
%可视化
p560.plot(q)
qplot(t, q); %绘制所有关节角的变化
%绘制笛卡尔空间的运动轨迹
T = p560.fkine(q);
p = T.transl;
plot(p(1,:), p(2,:)) %位置变化
plot(t, T.torpy('xyz')) %姿态变化XYZ roll-pitch-yaw
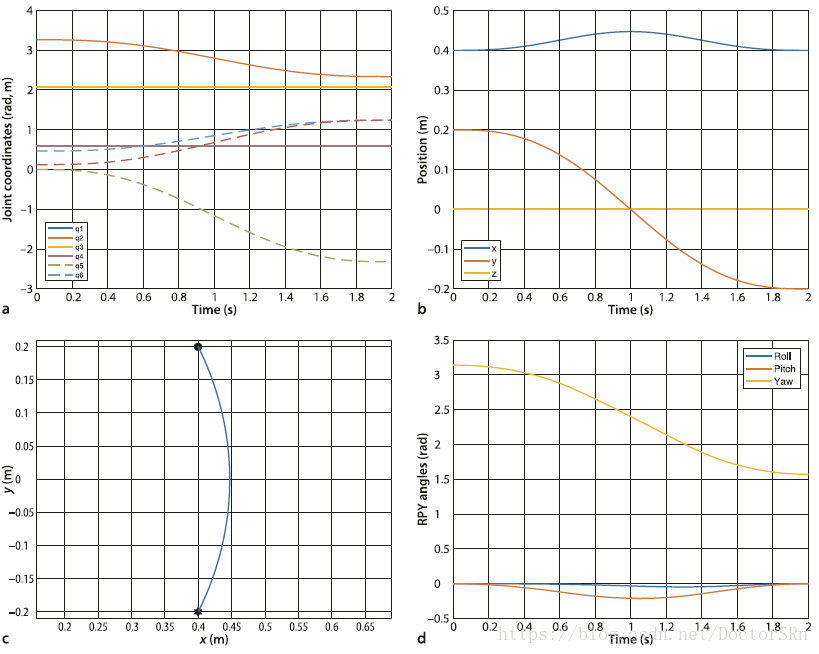
可以发现在关节空间的移动是平滑的。在笛卡尔空间末端执行器在x-y平面的移动轨迹不是直线,所以这是意料之中的,但这样移动可能导致碰撞,即使障碍物不在起始点和目标点之间。
7.3.2 Cartesian Motion 笛卡尔空间的运动
Matlab仿真程序:
%使用ctraj函数
Ts = ctraj(T1, T2, length(t));
plot(t, Ts.transl);
plot(t, Ts.torpy('xyz'));
%关节空间的变化
qc = p560.ikine6s(Ts);
p560.plot(qc)
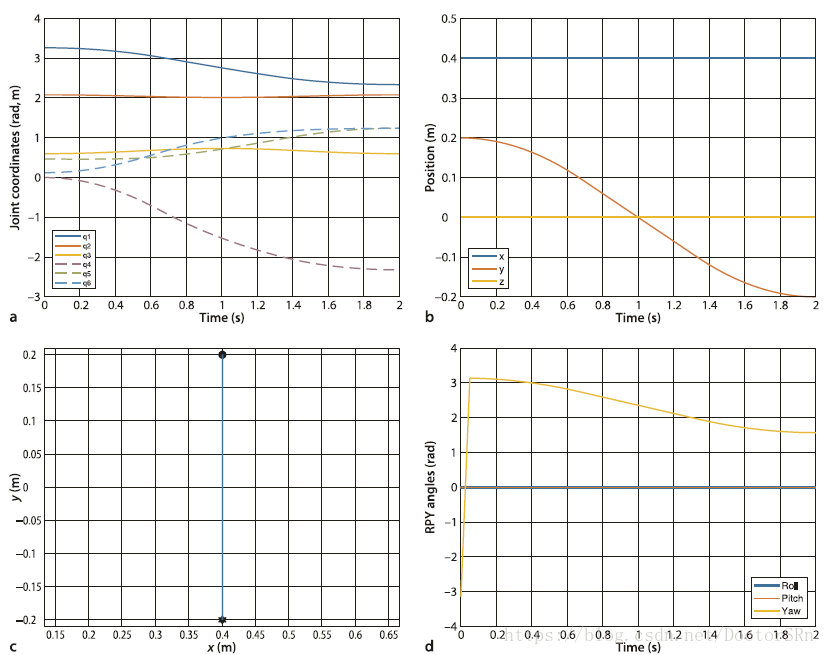
与关节空间的运动相比:末端执行器在x-y平面沿直线运动,同时roll和pitch角在路径上恒为0度。
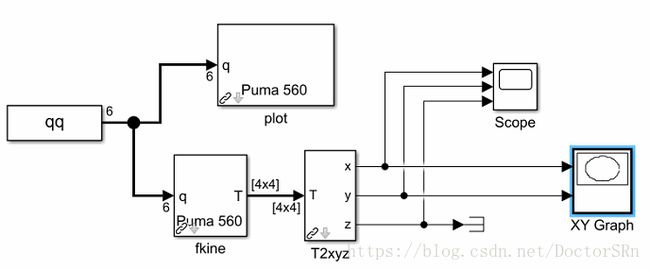
7.3.3 Kinematics in Simulink
使用simulink进行运动学仿真:sl_jspace
7.3.4 Motion through a Singularity
探究轨迹通过奇异点的运动:
mdl_puma560
%z轴指向直接坐标系的x轴
T1 = SE3(0.5, 0.3, 0.44) * SE3.Ry(pi/2);
T2 = SE3(0.5, -0.3, 0.44) * SE3.Ry(pi/2);
t = [0:0.05:2]';
%笛卡尔空间轨迹生成
Ts = ctraj(T1, T2, length(t));
%用解析解方法逆解算对应的关节角,对应图a
qc = p560.ikine6s(Ts);
%图d:qc的可操纵性
m = p560.maniplty(qc);
- 从图a可以看到在 q 5 q_5 q5=0附近 q 4 , q 6 q_4,q_6 q4,q6变化剧烈,这是因为 q 5 q_5 q5接近0度时, q 4 , q 6 q_4,q_6 q4,q6的旋转轴几乎平齐,发生万向节锁现象(也即奇异点)。关节轴对齐意味着机械臂丢失一个自由度,所以现在有效轴只有5轴(有效轴为5,实际关节角为6,相当于机械臂成为冗余机械臂),我们能确定的是 q 4 + q 6 q_4+q_6 q4+q6的和,而它们的具体取值有无数种。
- 图b是使用广义逆运动学方法ikine求解的结果,由于该方法会使用最小范数约束使 q 4 , q 6 q_4,q_6 q4,q6的范数值最小,同时满足 q 4 + q 6 q_4+q_6 q4+q6的和正确。
- 图c是这两个位姿在关节空间的运动,可以发现不存在奇异点问题,这是因为不涉及逆运动学过程。
- 图d是机械臂可操纵性图:
m = p560.maniplty(qc)。可操纵性:机械臂的灵活性,表征其在任意方向上容易移动的能力。是一个标量,可以计算轨迹上每个点的可操纵性值,越高越好。可以看到在奇异点附近可操纵性值接近0。可操纵性和广义逆运动学函数ikine都建立在机械臂Jacobian矩阵的基础上。
7.3.5 Configuration Change
之前讨论过机械臂左右手工作方式和肘部向上向下工作方式。比如左右手工作方式的图解:
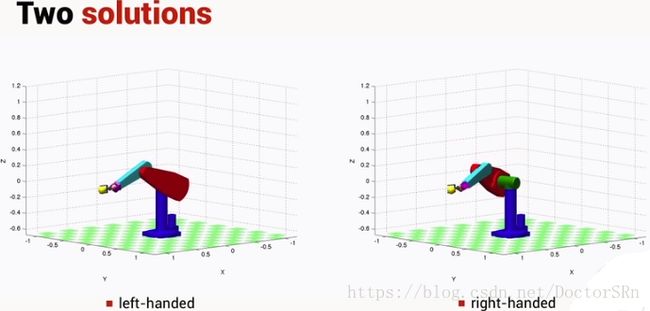
图片来自本书对应的公开课所对应的Configuration change章节。
如果从一个配置点运动至另一个配置点(比如从右手方式运动至左手方式),因为末端执行器对应的笛卡尔空间位姿一样,所以无法在笛卡尔空间进行轨迹规划,只能在关节空间进行轨迹规划。
Matlab示例程序:
T = SE3(0.4, 0.2, 0) * SE3.Rx(pi);
qr = p560.ikine6s(T, 'ru');
ql = p560.ikine6s(T, 'lu');
%从右手工作方式到左手工作方式的轨迹规划
q = jtraj(qr, ql, t);
p560.plot(q)
7.4 Advanced Topics
7.4.1 Joint Angle Offsets
零度关节角位姿(zero joint angles)是机械臂设计者任意确定的,甚至可能是不可达的位姿。下图是PUMA560的零度关节角位姿,这样定义零度关节角位姿是为了方便确定标准D-H参数:

而关节坐标偏移机制的存在可以任意设置零度关节坐标,设关节坐标偏移向量为 q 0 q_0 q0,则有:
ξ E = K ( q + q 0 ) \xi_E = \mathcal{K}(\mathbf{q}+\mathbf{q_0}) ξE=K(q+q0)
q = K − 1 ( ξ E ) − q 0 \mathbf{q} = \mathcal{K}^{-1}(\xi_E) -\mathbf{q_0} q=K−1(ξE)−q0
Matlab中通过设置Link对象的offset属性或者SerialLink结构的’offset’选项来赋值。
7.4.2 Determining Denavit-Hartenberg Parameters
确定D-H参数的经典方法是系统的为每个连杆分配一个坐标系,如PUMA560机械臂D-H参数的确定。但是这种方法设置每个坐标系时存在很强的局限性,因为关节必须绕z轴转动且连杆的移动必须沿着x轴方向,这又对基座和末端执行器的坐标系的放置施加了约束,并最终决定了零角度位姿。所以说确定一个D-H参数对应的连杆坐标系比确定D-H参数本身更难。
在Matlab Toolbox的支持下,一个可选的方法是:将机械臂简单描述为从基座到末端执行器的一系列基本的平移和旋转变换,其中有一些基本变换是恒定的,比如平移变换代表连杆的长度或者偏移,还有一些是广义关节坐标的函数。这种方法和之前所说的传统方法相比,对旋转或平移的轴没有进行约束。
以PUMA560为例,MATLAB程序:
%使用string平移和旋转变换序列
s = 'Tz(L1) Rz(q1) Ry(q2) Ty(L2) Tz(L3) Ry(q3) Tx(L4) Ty(L5)
Tz(L6) Rz(q4) Ry(q5) Rz(q6)'
%将string输入到字符代数函数
%该函数将机械臂的运动学结构分解为标准的D-H参数
dh = DHFactor(s);
%显示各个关节的D-H参数
dh
%使用得到的D-H参数生成对应的机械臂模型
%生成名为puma的机械臂模型对应的matlab命令
cmd = dh.command('puma')
%执行上述生成的命令,生成机器人模型
robot = eval(cmd)
可以看到上述程序在描述第二个关节时使用"Ry(q2)",这在传统方法D-H形式主义中是不允许(D-H形式主义要求旋转必须绕z轴)。
7.4.3 Modified Denavit-Hartenberg Parameters 改进型D-H参数
改进型D-H参数与普通的D-H参数相比:前者连杆坐标系连接到每个连杆的近端(近端)而不是远端(远端)。这种改进使符号在某些方面更加清晰和整洁。D-H参数的定义直接影响到运动学、Jacobian行列式和动力学算法。
改进型D-H参数约定的连杆见变换矩阵为:
j − 1 ξ j ( α j − 1 , a j − 1 , d j , θ j ) = R x ( α j − 1 ) ⊕ T x ( a j − 1 ) ⊕ T z ( d j ) ⊕ R z ( θ j ) ^{j-1}\xi_j(\alpha_{j-1},a_{j-1},d_j,\theta_j)= \mathcal{R}_x(\alpha_{\tiny{j-1}}) \oplus \mathcal{T}_x(a_{\tiny{j-1}}) \oplus \mathcal{T}_z(d_{\tiny{j}}) \oplus \mathcal{R}_z(\theta_{\tiny{j}}) j−1ξj(αj−1,aj−1,dj,θj)=Rx(αj−1)⊕Tx(aj−1)⊕Tz(dj)⊕Rz(θj)
改进型D-H参数坐标系定义图示:
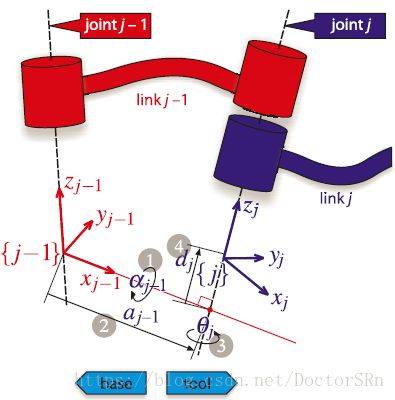
Note: 使用论文中提供的D-H参数建立机器人模型时,首先需要确定该论文使用的是哪一种约定的参数表达方式。一般来说,表头是 θ j , d j , a j , α j \theta_j,d_j,a_j,\alpha_j θj,dj,aj,αj的是标准D-H参数形式,表头是 θ j , d j , a j − 1 , α j − 1 \theta_j,d_j,a_{j-1},\alpha_{j-1} θj,dj,aj−1,αj−1的是改进型D-H参数。
在Matlab中使用L1 = RevoluteMDH('d', 1)来建立一个使用改进型D-H(MDH)参数的旋转铰链结构模型,然后就可以进一步建立完整的机械臂模型。
标准D-H参数和改进型D-H参数的联系:
设标准D-H参数的表达式为:
R z ( θ 1 ) ⊕ T z ( d 1 ) ⊕ T x ( a 1 ) ⊕ R x ( α 1 ) ⎵ D H 1 ⊕ R z ( θ 2 ) ⊕ T z ( d 2 ) ⊕ T x ( a 2 ) ⊕ R x ( α 2 ) ⎵ D H 2 ⋯ \underbrace{\mathcal{R}_z(\theta_{\tiny{1}}) \oplus \mathcal{T}_z(d_{\tiny{1}}) \oplus \mathcal{T}_x(a_{\tiny{1}}) \oplus \mathcal{R}_x(\alpha_{\tiny{1}})}_{DH_1} \oplus \underbrace{\mathcal{R}_z(\theta_{\tiny{2}}) \oplus \mathcal{T}_z(d_{\tiny{2}}) \oplus \mathcal{T}_x(a_{\tiny{2}}) \oplus \mathcal{R}_x(\alpha_{\tiny{2}})}_{DH_2} \cdots DH1 Rz(θ1)⊕Tz(d1)⊕Tx(a1)⊕Rx(α1)⊕DH2 Rz(θ2)⊕Tz(d2)⊕Tx(a2)⊕Rx(α2)⋯
改进型D-H参数的表达式可由上式重写为:
R z ( θ 1 ) ⊕ T z ( d 1 ) ⎵ b a s e ⊕ T x ( a 1 ) ⊕ R x ( α 1 ) ⊕ R z ( θ 2 ) ⊕ T z ( d 2 ) ⎵ M D H 1 ⊕ T x ( a 2 ) ⊕ R x ( α 2 ) ⋯ ⎵ M D H 2 \underbrace{\mathcal{R}_z(\theta_{\tiny{1}}) \oplus \mathcal{T}_z(d_{\tiny{1}})}_{base} \oplus \underbrace{ \mathcal{T}_x(a_{\tiny{1}}) \oplus \mathcal{R}_x(\alpha_{\tiny{1}}) \oplus \mathcal{R}_z(\theta_{\tiny{2}}) \oplus \mathcal{T}_z(d_{\tiny{2}})}_{MDH_1} \oplus \underbrace{\mathcal{T}_x(a_{\tiny{2}}) \oplus \mathcal{R}_x(\alpha_{\tiny{2}}) \cdots}_{MDH_2} base Rz(θ1)⊕Tz(d1)⊕MDH1 Tx(a1)⊕Rx(α1)⊕Rz(θ2)⊕Tz(d2)⊕MDH2 Tx(a2)⊕Rx(α2)⋯
其中 M D H j MDH_j MDHj的形式与
j − 1 ξ j ( α j − 1 , a j − 1 , d j , θ j ) = R x ( α j − 1 ) ⊕ T x ( a j − 1 ) ⊕ T z ( d j ) ⊕ R z ( θ j ) ^{j-1}\xi_j(\alpha_{j-1},a_{j-1},d_j,\theta_j)= \mathcal{R}_x(\alpha_{\tiny{j-1}}) \oplus \mathcal{T}_x(a_{\tiny{j-1}}) \oplus \mathcal{T}_z(d_{\tiny{j}}) \oplus \mathcal{R}_z(\theta_{\tiny{j}}) j−1ξj(αj−1,aj−1,dj,θj)=Rx(αj−1)⊕Tx(aj−1)⊕Tz(dj)⊕Rz(θj)
是等价的,因为沿着同一个轴进行平移和旋转的变换是可以交换的,即满足:
R i ( θ ) ⊕ T i ( d ) = T i ( d ) ⊕ R i ( θ ) , i ∈ { x , y , z } R_i(\theta) \oplus T_i(d) = T_i(d) \oplus R_i(\theta), \, i \in \left \{ x,y,z \right \} Ri(θ)⊕Ti(d)=Ti(d)⊕Ri(θ),i∈{x,y,z}
7.5 Applications
7.5.1 Writing on a Surface [examples/drawing.m]
使用Hershey font作为字体输入数据。
Matlab程序:
%载入hershy字体数据
load hershey
%载入‘B’的字体数据
B = hershey{'B'};
%两行数据分别代表x,y轴的点,NaN表示分段点--起笔或落笔点
B.stroke
%将坐标乘以0.25,限制路径在0.85*0.25cm的范围内,,并添加z轴
%将Nan点替换为其上一时刻的坐标
path = [ 0.25*B.stroke; zeros(1,numcols(B.stroke))];
k = find(isnan(path(1,:)));
path(:,k) = path(:,k-1); path(3,k) = 0.2;
%使用mstraj进行多段轨迹规划,更多信息help mstraj查看
traj = mstraj(path(:,2:end)', [0.5 0.5 0.5], [], path(:,1)', 0.02, 0.2);
%得到路径的信息
about(traj)
%沿此路径移动的时间
numrows(traj) * 0.02
%将该轨迹可视化
plot3(traj(:,1), traj(:,2), traj(:,3))
通过上面的程序得到的只是轨迹的位置序列,为了使用PUMA560绘制该轨迹,需要添加姿态信息,我们设置绘制平面为x-y平面(水平面),其末端执行的z向矢量(approach vector)为 a = [ 0 , 0 , − 1 ] a=[0,0,-1] a=[0,0,−1],y向矢量(orientation vector)为 o = [ 010 ] o=[0 1 0] o=[010],同时将绘制的起点设为[0.6,0,0],对应的Matlab程序为:
Tp = SE3(0.6, 0, 0) * SE3(traj) * SE3.oa( [0 1 0], [0 0 -1]);
q = p560.ikine6s(Tp);
%设置显示轨迹
p560.plot(q, 'trail',{'r', 'LineWidth', 2})
此外也可以使用simulink模块进行绘制,步骤如下:
-
使用
sl_jspace打开simulink示例模型,将其输入部分替换为From Workspace模块,按照该模块的配置要求在工作空间中设置好导入的数据。我们需要导入的是之前生成的轨迹对应的关节坐标序列q,按照From Workspace模块配置要求设置新变量:qq.time = [] qq.signals.values = q qq.signals.dimensions = 6;
7.5.2 A Simple Walking Robot [examples/walking.m]
本章搭建一个行走机器人。行走机器人的腿和机械臂类似,由于脚与地面有点接触且朝向重要,所以三关节串联结构足以满足要求。
Kinematics
下图是行走机器人的零位示意图:

第一个关节负责前后运动,旋转轴是z轴,旋转变换 R z ( q 1 ) R_z(q_1) Rz(q1);第二个关节负责上下运动,旋转轴是x轴,旋转变换是 R x ( q 2 ) R_x(q_2) Rx(q2);第三个关节式膝盖,负责远离或者靠近身体,旋转变换是 R x ( q 3 ) R_x(q_3) Rx(q3)。则从臀部至脚趾的变换序列是:
ξ = R z ( q 1 ) R x ( q 2 ) T y ( L 1 ) R x ( q 3 ) T z ( L 2 ) \xi = R_z(q_1)R_x(q_2)T_y(L_1)R_x(q_3)T_z(L_2) ξ=Rz(q1)Rx(q2)Ty(L1)Rx(q3)Tz(L2)
使用Matlab建立模型:
s = 'Rz(q1) Rx(q2) Ty(L1) Rx(q3) Tz(L2)';
%得到标准D-H参数,最后三项为末端Tool朝向变换,无关紧要
dh = DHFactor(s)
%D-H后三项
dh.tool
%得到建立模型的MATLAB指令
dh.command('leg')
%建立模型
L1 = 0.1; L2 = 0.1;
leg = eval( dh.command('leg') )
%零位下脚的位置
transl( leg.fkine([0,0,0]) )
%可视化零位
leg.plot([0,0,0], 'nobase', 'noshadow', 'notiles')
set(gca, 'Zdir', 'reverse'); view(137,48);
Motion of One Leg
接下来确定末端执行器–脚的移动路径。考虑行走机器人向前移动的过程:
- 所有脚以同样的速度向后移动,重置腿的位置–将脚抬起向前移动后放下,重复上述动作
- 为保持机器人的稳定,需要至少三只脚在地上,所以需要依次重置腿的位置
Matlab程序:
%xf,xb是前后移动(沿x轴)的限制,单位mm
%y是脚和身体之间的距离(沿y轴)
%zu,zd是脚上下移动的相对高度(沿z轴)
xf = 50; xb = -xf; y = 50; zu = 20; zd = 50;
%得到路径
path = [xf y zd; xb y zd; xb y zu; xf y zu; xf y zd] * 1e-3;
%轨迹规划
p = mstraj(path, [], [0, 3, 0.25, 0.5, 0.25]', path(1,:), 0.01, 0);
%使用逆运动学解算关节坐标
qcycle = leg.ikine( SE3(p), 'mask', [1 1 1 0 0 0] );
leg.plot(qcycle, 'loop')
脚移动时x,z轴的变化,以及四个脚再向前移动过程中x轴方向的位移图像:
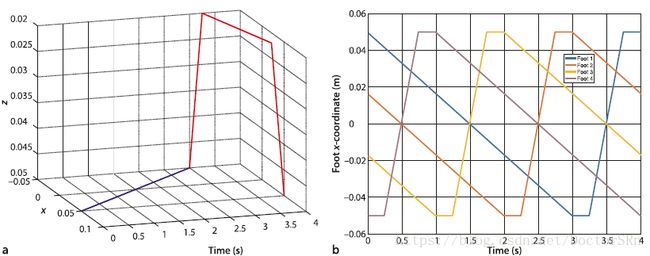
Motion of Four Legs
Matlab程序:
W = 0.1; L = 0.2;
legs(1) = SerialLink(leg, 'name', 'leg1');
legs(2) = SerialLink(leg, 'name', 'leg2', 'base', SE3(-L, 0, 0));
legs(3) = SerialLink(leg, 'name', 'leg3', 'base', SE3(-L, -W, 0) * SE3.Rz(pi));
legs(4) = SerialLink(leg, 'name', 'leg4', 'base', SE3(0, -W, 0) * SE3.Rz(pi));
clf; k = 1;
while 1
legs(1).plot( gait(qcycle, k, 0, false) );
if k == 1, hold on; end
legs(2).plot( gait(qcycle, k, 100, false) );
legs(3).plot( gait(qcycle, k, 200, true) );
legs(4).plot( gait(qcycle, k, 300, true) );
drawnow
k = k+1;
end
完整的Walking程序:
%walking
clear all
L1 = 0.1; L2 = 0.1;
% create the leg links based on DH parameters
% theta d a alpha
links(1) = Link([ 0 0 0 pi/2 ], 'standard');
links(2) = Link([ 0 0 L1 0 ], 'standard');
links(3) = Link([ 0 0 -L2 0 ], 'standard');
% now create a robot to represent a single leg
leg = SerialLink(links, 'name', 'leg', 'offset', [pi/2 0 -pi/2]);
% define the key parameters of the gait trajectory, walking in the
% x-direction
xf = 5; xb = -xf; % forward and backward limits for foot on ground
y = 5; % distance of foot from body along y-axis
zu = 2; zd = 5; % height of foot when up and down
% define the rectangular path taken by the foot
segments = [xf y zd; xb y zd; xb y zu; xf y zu] * 0.01;
% build the gait. the points are:
% 1 start of walking stroke
% 2 end of walking stroke
% 3 end of foot raise
% 4 foot raised and forward
%
% The segments times are :
% 1->2 3s
% 2->3 0.5s
% 3->4 1s
% 4->1 0.5ss
%
% A total of 4s, of which 3s is walking and 1s is reset. At 0.01s sample
% time this is exactly 400 steps long.
%
% We use a finite acceleration time to get a nice smooth path, which means
% that the foot never actually goes through any of these points. This
% makes setting the initial robot pose and velocity difficult.
%
% Intead we create a longer cyclic path: 1, 2, 3, 4, 1, 2, 3, 4. The
% first 1->2 segment includes the initial ramp up, and the final 3->4
% has the slow down. However the middle 2->3->4->1 is smooth cyclic
% motion so we "cut it out" and use it.
segments = [0 0 0;segments; segments];
tseg = [3 0.25 0.5 0.25]';
tseg = [1;tseg; tseg];
x = mstraj(segments, [], tseg, segments(1,:), 0.01, 0.1);
% pull out the cycle
xcycle = x(100:500,:);
qcycle = leg.ikine( transl(xcycle), 'mask', [1 1 1 0 0 0] );
% dimensions of the robot's rectangular body, width and height, the legs
% are at each corner.
W = 0.1; L = 0.2;
% a bit of optimization. We use a lot of plotting options to
% make the animation fast: turn off annotations like wrist axes, ground
% shadow, joint axes, no smooth shading. Rather than parse the switches
% each cycle we pre-digest them here into a plotopt struct.
% plotopt = leg.plot({'noraise', 'nobase', 'noshadow', ...
% 'nowrist', 'nojaxes'});
% plotopt = leg.plot({'noraise', 'norender', 'nobase', 'noshadow', ...
% 'nowrist', 'nojaxes', 'ortho'});
plotopt = {'noraise', 'nobase', 'noshadow', 'nowrist', 'nojaxes', 'delay', 0};
% create 4 leg robots. Each is a clone of the leg robot we built above,
% has a unique name, and a base transform to represent it's position
% on the body of the walking robot.
legs(1) = SerialLink(leg, 'name', 'leg1');
legs(2) = SerialLink(leg, 'name', 'leg2', 'base', transl(-L, 0, 0));
legs(3) = SerialLink(leg, 'name', 'leg3', 'base', transl(-L, -W, 0)*trotz(pi));
legs(4) = SerialLink(leg, 'name', 'leg4', 'base', transl(0, -W, 0)*trotz(pi));
% create a fixed size axis for the robot, and set z positive downward
clf; axis([-0.3 0.1 -0.2 0.2 -0.15 0.05]); set(gca,'Zdir', 'reverse')
hold on
% draw the robot's body
patch([0 -L -L 0], [0 0 -W -W], [0 0 0 0], ...
'FaceColor', 'r', 'FaceAlpha', 0.5)
% instantiate each robot in the axes
for i=1:4
legs(i).plot(qcycle(1,:), plotopt{:});
end
hold off
% walk!
k = 1;
%A = Animate('walking');
%while 1
for i=1:500
legs(1).animate( gait(qcycle, k, 0, 0));
legs(2).animate( gait(qcycle, k, 100, 0));
legs(3).animate( gait(qcycle, k, 200, 1));
legs(4).animate( gait(qcycle, k, 300, 1));
drawnow
k = k+1;
%A.add();
end