线性回归 & Softmax与分类模型 & 多层感知机

目录

一、线性回归

1 线性回归

2 动手实践

2.1 尽量使用矢量/矩阵运算，提高计算效率

2.2  Pytorch 梯度累积机制

二 Softmax与分类模型

1 Softmax

2 分类模型

3 动手实践

（1）广播机制

（2）关于softmax函数

3 测验题

三 多层感知机

1 多层感知机

2 激活函数

---

一、线性回归

大学的时候，统计学专业，线性回归这个内容足足有一本书，包含了很多内容。《动手学深度学习》这本书，书如其名，侧重于实践。

1 线性回归

统计学习方法=模型+策略+算法，下面就从这三部分对线性回归进行描述。

待更新

 

2 动手实践

实现一个模型的pipeline包括以下几个部分：

1 准备数据集

2 数据读取

3 定义模型

4 定义损失函数

5 定义优化器/优化函数

6 参数初始化

参数初始化方法有很多，什么？你想要初始化为一个常数？你摊上大事了！！！

如果初始化后同一层神经元的参数都相同，那么在模型训练时，该层中每个神经元将根据相同输入计算出相同的输出，反向传播时梯度都一样，这种情况下，无论该层神经元有多少，本质上只有1个神经元在发挥作用。
 

7 模型训练

8 模型预测

这里不详细写每一步的具体实现，只总结一些编程中的二三事：

2.1 尽量使用矢量/矩阵运算，提高计算效率

为了提高计算效率，尽量避免用for循环，应尽可能的使用矢量运算。这是因为for循环是串行的，而工具库封装的向量运算、矩阵运算等是做了优化的，比如并行实现，所以效率会更高。

2.2  Pytorch 梯度累积机制

对于求解数值解，都需要用到梯度计算与梯度更新（对各个参数同时进行更新），若使用Pytorch，要格外注意一件事情，那就是每轮迭代要记得梯度清零，因为Pytorch中实现的梯度计算是累积梯度。若使用tensorflow就不需要梯度清0了，因为它计算的就是当前batch中的梯度。

l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # reset gradient
l.backward()  # compute gradient
optimizer.step() # update gradient

也许你要问了，既然还要显式梯度清零这么麻烦，为什么pytorch还要这么设计呢？因为有时候我们会用到梯度累加。当你GPU显存较少时，你又想要调大batch-size，此时你就可以利用梯度累加来进行backward，在每次反向传播后，先不进行优化器的迭代，多累积几个batch的梯度后，再进行优化器迭代、梯度清零的操作。这样做可以达到用时间换效果的目的。

二 Softmax与分类模型

Softmax常用于多分类模型

1 Softmax

待更新

 

2 分类模型

统计学习方法 = 模型+策略+算法

策略，即如何定义损失函数，分类模型中常用交叉熵损失函数，那么，为什么用交叉熵损失函数而不用平方损失函数呢？

 

 

3 动手实践

仅记录一些编程中的二三事。

（1）广播机制

什么是广播机制？以下介绍复制于《动手学深度学习》

                                      

了解了广播机制的定义，那么为什么要用广播机制呢？自然是为了进行矢量运算加快计算效率。下图同样来源于《动手学深度学习》，如果没有广播机制，XW与b的维度不同，不能直接进行矩阵运算。

                            

（2）关于softmax函数

softmax函数在使用时，容易出现上溢或者下溢，为了保证数值稳定性，根据性质softmax(x) = softmax(x-c)，c常取为max(x),对softmax进行如下实现：

def softmax(x):
    """Compute the softmax function for each row of the input x.

    Numpy broadcasting documentation:
    http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html

    Arguments:
    x -- A D dimensional vector or N x D dimensional numpy matrix.

    Return:
    x -- You are allowed to modify x in-place
    """

    if len(x.shape) > 1:
        # Matrix
        f = lambda vec: np.exp(vec)/np.sum(np.exp(vec))
        # numpy.apply_along_axis(func, axis, arr)是一个根据func()函数以及维度axis运算后得到的的数组.
        x -= np.max(x, 1).reshape(-1, 1)
        x = np.apply_along_axis(f, 1, x)  # 1表示按行运算，x是一个二维数组，即矩阵

    else:
        # Vector
        x -= np.max(x)
        x = np.exp(x)/np.sum(np.exp(x))

    return x

3 测验题

关于第二题，本节课每个epoch结束后计算并输出测试集上的准确率，在epoch过程中，每个batch迭代完就计算一次该batch上的准确率，等整个epoch结束计算总的准确率并输出。具体代码见《动手学深度学习》。

三 多层感知机

多层感知机（MLP）是基础中的基础，直接做问答题好了=-=

1 多层感知机

                                         

1 上图所示感知机能否解决异或（XOR）问题？

 

2 激活函数

1 为什么使用激活函数？

全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）

2 激活函数及其优缺点

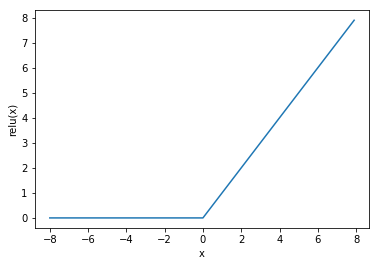
①Relu

             

               

 

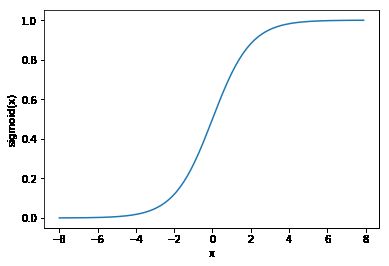
② Sigmoid 将元素的值变换到0和1之间

               

                  

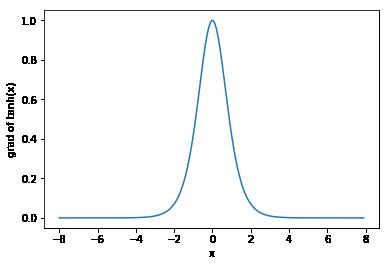
③tanh 双曲正切函数

                

               

激活函数的选择：

ReLu函数是一个通用的激活函数，目前在大多数情况下使用。但是，ReLU函数只能在隐藏层中使用，用于二分类时，sigmoid函数与Relu组合通常效果更好。

由于梯度消失问题，有时要避免使用sigmoid和tanh函数。

在神经网络层数较多的时候，最好使用ReLu函数，ReLu函数比较简单计算量少，而sigmoid和tanh函数计算量大很多。

在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。