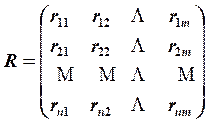数学建模之MATLAB编程

EverydayOneCat

✖️N


「Sushi shop!」

知识点

1.下载

链接：https://pan.baidu.com/s/1DbfysOOwIoSvt8HQUw0jhw
提取码：75mz

2.基本数学运算

2.1变量与数据操作

变量定义注意事项：

• 变量名区分字母大小写
• 变量名必须以字母开头，之后可以是任意字母、数字或下划线
• MATLAB语言将所识别的一切变量视为局部变量，若要将变量定义为全局变量，则应当对变量进行说明，即在该变量前加关键字global.

特殊变量表：

特殊变量	取值
ans	用于结果的缺省变量名
pi	圆周率
eps	计算机的最小数
flops	浮点运算数
inf	无穷大 如1/0
nan	不等量 如0/0
i j	i=j=虚数单位
nargin	函数的输入变量数目
nargout	函数的输出变量数目
realmin	最小的可用正实数
realmax	最大的可用正实数

2.2MATLAB常用数学函数

MATLAB 提供了许多数学函数，函数的自变量规定为矩阵变量，运算法则是将函数逐项作用于矩阵的元素上，因而运算的结果是一个与自变量同维数的矩阵。

1．基本数学函数：

abs(x)：纯量的绝对值或向量的长度

angle(z)：复数z的相角**(Phase angle) sqrt(x)：开平方 real(z)：复数z**的实部

imag(z)：复数z的虚部

conj(z)：复数z的共轭复数

round(x)：四舍五入至最近整数

fix(x)：无论正负，舍去小数至最近整数

floor(x)：地板函数，即舍去正小数至最近整数

ceil(x)：天花板函数，即加入正小数至最近整数

rat(x)：将实数x化为分数表示

rats(x)：将实数x化为多项分数展开

rem(x,y)：求x除以y的余数

gcd(x,y)：整数x和y的最大公因数

lcm(x,y)：整数x和y的最小公倍数

exp(x)：自然指数

pow2(x)：2的指数

log(x)：以e为底的对数，即自然对数

log2(x)：以2为底的对数

log10(x)：以10为底的对数

sign(x)：符号函数 (Signum function).

2．三角函数：

sin(x)：正弦函数 cos(x)：余弦函数

tan(x)：正切函数 asin(x)：反正弦函数

acos(x)：反余弦函数 atan(x)：反正切函数

atan2(x,y)：四象限的反正切函数 sinh(x)：超越正弦函数

cosh(x)：超越余弦函数 tanh(x)：超越正切函数

asinh(x)：反超越正弦函数 acosh(x)：反超越余弦函数atanh(x)：反超越正切函数

3．适用于向量的常用函数：

min(x): 向量x的元素的最小值 max(x): 向量x的元素的最大值

mean(x): 向量x的元素的平均值 median(x): 向量x的元素的中位数

std(x): 向量x的元素的标准差 diff(x): 向量x的相邻元素的差

sort(x): 对向量x的元素进行排序（Sorting） length(x): 向量x的元素个数

norm(x): 向量x的欧氏长度 sum(x): 向量x的元素总和

prod(x): 向量x的元素总乘积 cumsum(x): 向量x的累计元素总和

cumprod(x): 向量x的累计元素总乘积 dot(x, y): 向量x和y的内积

cross(x, y): 向量x和y的外积

+++

例：随机抽取10 名学生的高等数学课程成绩，并统计他们中的最高分、最低分以及他们的平均成绩。

>> math=[88,90,77,69,92,80,74,66,95,85]; %产生10维向量
mathaver=sum(math)/10 %计算平均成绩
h=max(math) %求出最高分
l=min(math) %求出最低分

2.3MATLAB矩阵

矩阵的建立：

（1）直接输入法——A=[1 2 3；4 5 6；7 8 9]

矩阵同行元素之间由空格或逗号分隔，行与行之间用分号或回车键分隔；若“[ ]”中无元素表示空矩阵.

（2）利用冒号和函数——函数linspace（a，b，n）产生第一个元素为a，最后一个元素为b总数为n的行向量

>> a=1:0.5:4 % 格式是初始值：步长：终止值
a=
Columns １ through 7
1 1.5 2 2.5 3 3.5 4

（3）矩阵合并

>> B=[1 1 1]
B =
1 1 1
>> C=[A;B]	%分号增加行
C =
1 2 3
4 5 6
7 8 9
1 1 1
>> D=[A,B']	%逗号增加列
D =
1 2 3 1
4 5 6 1
7 8 9 1

矩阵的截取：

（1） 矩阵元素

>> A(2,3) %下标引用
ans = 6
>> A(6)	%一列一列的开始数
ans = 8

序号(Index)与下标(Subscript )是一一对应的，其相互转换关系也可利用sub2ind和ind2sub函数求得。

>> sub2ind(size(A),2,3)
ans= 8
[i,j]=ind2sub(size(A),8)
i= 2
j= 3

（2） 使用冒号

可以用冒号表示“直到”以及“所有行”，“所有列”，还可利用一般向量和end运算符来表示矩阵下标，从而获得子矩阵。end表示某一维的末尾元素下

>> B=A (1:2, : ) %逗号前面是行数，表示第一行直到第二行；逗号后面列数，表示所有列
B=
1 2 3
4 5 6

>> C=A([1,3],2:end)	%行数：第一行和第三行；列数：第二列直到最后
C =
2 3
8 9

+++

特殊矩阵：

zeros(m,n)	生成一个 m 行 n 列的零矩阵，m=n 时可简写为 zeros(n)
ones(m,n)	生成一个 m 行 n 列的元素全为 1 的矩阵, m=n 时可写为 ones(n)
eye(m,n)	生成一个主对角线全为 1 的 m 行 n 列矩阵, m=n 时可简写为 eye(n)，即为 n 维单位矩阵
diag(X)	若 X 是矩阵，则 diag(X) 为 X 的主对角线向量 若 X 是向量，diag(X) 产生以 X 为主对角线的对角矩阵
tril(A)	提取一个矩阵的下三角部分
triu(A)	提取一个矩阵的上三角部分
rand(m,n)	产生 0～1 间均匀分布的随机矩阵 m=n 时简写为 rand(n)
randn(m,n)	产生均值为0，方差为1的标准正态分布随机矩阵 m=n 时简写为 randn(n)

例：

分别建立3×3、3×2和与矩阵A同样大小的零矩阵。

>> zeros(3)，zeros(3,2)，zeros(size(A))

建立随机矩阵：
(1) 在区间[20,50]内均匀分布的5阶随机矩阵。
(2) 均值为0.6、方差为0.1的5阶正态分布随机矩阵。

>> x=20+(50-20)*rand(5)
y=0.6+sqrt(0.1)*randn(5)

3.MATLAB运算

3.1基本算术运算

MATLAB的基本算术运算有：＋(加)、－(减)、*(乘)、/(右除)、\ (左除)、^(乘方)。

这个就是矩阵的乘法，线性代数知识：m* n的矩阵只有和n *x的矩阵才能相乘得出m *x的矩阵。(老汤别打我，我只记得这个了)

3.2点运算

在MATLAB中，有一种特殊的运算，因为其运算符是在有关算术运算符前面加点，所以叫点运算。

点运算符有:
点乘： .*
点除： ./ .
点幂： .^

两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵的维数相同。

>> A.^2
ans =
1 4 9
16 25 36
49 64 81

符号运算符	功 能	类别
= =	等于	关系运算符
~ =	不等于
<	小于
>	大于
<=	小于等于
>=	大于等于
&	逻辑与	逻辑运算符
|	逻辑或
~	逻辑非

例:

产生5阶随机方阵A，其元素为[10,90]区间的随机整数，然后判断A的元素是否能被3整除。

>> A=fix((90-10+1)*rand(5)+10) %生成5阶随机方阵A
P=rem(A,3)==0 %判断结果是一个布尔矩阵

fix()取整；rand生成0~1的随机方阵；rem(A,B)——A/B的余数

建立矩阵A，然后找出大于4的元素的位置。

>> A=[4,-65,-54,0,6;56,0,67,-45,0]
find(A>4) %返回的是索引值

3.3矩阵分析

用求逆矩阵的方法解线性方程组。备注：Ax=b其解为：x=A-1b

>> a=[2,-3,1;8,3,2;45,1,-9];
b=[4;2;17]; x=inv(a)*b

用求特征值的方法解方程：
$$3x^5-7x^4+5x^2+2x-18=0$$

>> p=[3,-7,0,5,2,-18];
A=compan(p); %友矩阵A，特征值与多项式根一样
x1=eig(A) %求A的特征值
x2=roots(p) %直接求多项式p的零点

4.MATLAB程序设计

4.1M文件

所谓M文件就是由MATLAB语言编写的可在MATLAB语言环境下运行程序源代码文件。

M文件可以根据调用方式的不同分为两类：
命令文件(Script File)：自动重复执行的一组MATLAB命令和函数组合，不需输出输入参数。
函数文件(Function File)：M文件的第一个可执行以function开始，便是函数文件，每一个函数文件定义一个函数。

例一：分别建立命令文件和函数文件，将华氏温度f转换为摄氏温度c。

命令文件：

clear; %清除工作空间中的变量
f=input('temperature：');
c=5*(f-32)/9

函数文件：

function c=demo2(f)
c=5*(f-32)/9;

命令窗口输入：

>> c=f2c_fun(20)
c =
-6.6667

注意：函数只能调用，不能直接运行，函数调用的一般格式是：[输出实参表]=函数名(输入实参表)实参传递给形参

同时，如果需要测试多个变量，只有函数才能实现。

>> f=[20,73];c=demo2(f)
c =
-6.6667   22.7778

+++

例二：编写函数文件求半径为r的圆的面积和周长。

编写函数文件：

function [s,p]=demo3(r)
%r 圆半径
%s 圆面
%p 圆周长
s=pi*r*r;
p=2*pi*r;

我们这里计算半径为2和3的面积和周长，命令行输入：

>> r=[2,3];[s,p]=demo3(r)
错误使用  * 
用于矩阵乘法的维度不正确。请检查并确保第一个矩阵中的列数与第二个矩阵中的行数匹配。要执行按元素相乘，请使用 '.*'。

出错 demo3 (line 5)
s=pi*r*r;

发现出错，根据提示我们发现需要用点乘才能计算

%s=pi*r*r;
s=pi*r.*r;

>> r=[2,3];[s,p]=demo3(r)
s =
12.5664   28.2743
p =
12.5664   18.8496

4.2输入输出

1. 数据的输入

   从键盘输入数据：A=input(‘提示信息’，‘s’)；加上‘s’选项，则允许用户输入一个字符串。

>> xm=input('What''s your name?','s');
What's your name?张三

2. 数据的输出

disp(输出项)——其中输出项既可以为字符串，也可以为矩阵。

求一元二次方程ax2 +bx+c=0的根。

>> a=input('a=?');
b=input('b=?');
c=input('c=?');
d=b*b-4*a*c;
x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)];%sqrt——平方根
disp(['x1=',num2str(x(1)),',x2=', num2str(x(2))]);%num2str——数字转为字符串
a=?1
b=?3
c=?2
x1=-1,x2=-2

4.3选择结构

4.3.1if语句：

例一：

随机变量x = {0，1，2}表示每分钟到达超市收款台的人数，有分布列

xk	0	1	2
pk	0.4	0.3	0.3

模拟十分钟内顾客到达收款台的状况.

r=rand(1,10);%生成10个0~1随机数，代表每分钟来人的pk
for i=1:10
    if r(i)<0.4
        n(i)=0;
    elseif 0.4> demo5
r =
    0.7060    0.0318    0.2769    0.0462    0.0971    0.8235    0.6948    0.3171    0.9502	0.0344    
n =
     2     0     0     0     0     2     1     0     2     0

4.3.2switch语句：

例二：

某商场对顾客所购买的商品实行打折销售，标准如下(商品价格用price来表示)：
price<200 没有折扣
200≤price<500 3%折扣
500≤price<1000 5%折扣
1000≤price<2500 8%折扣
2500≤price<5000 10%折扣
5000≤price 14%折扣
输入所售商品的价格，求其实际销售价格。

price=input('请输入商品价格');
switch fix(price/100)
case {0,1} %价格小于200
rate=0;
case {2,3,4} %价格大于等于200但小于500
rate=3/100;
case num2cell(5:9) %价格大于等于500但小于1000
rate=5/100;
case num2cell(10:24) %价格大于等于1000但小于2500
rate=8/100;
case num2cell(25:49) %价格大于等于2500但小于5000
rate=10/100;
otherwise %价格大于等于5000
rate=14/100;
end
price=price*(1-rate) %输出商品实际销售价格

请输入商品价格656
price =
  623.2000

num2cell函数：num2cell(A)是把A中的每一个元素作为cell的元素，这样每个元素是一个数；

4.3.3for语句

其中表达式1 的值为循环变量的初值，表达式2的值为步长，表达式3的值为循环变量的终值。步长为1时，表达式2可以省略。

执行过程是依次将矩阵的各列元素赋给循环变量，然后执行循环体语句，直至各列元素处理完毕。

例三：

y=0;
n=100;
for i=1:n
    y=y+1/(2*i-1);
end
y

写出下列程序的执行结果

>> s=0;
a=[12,13,14;15,16,17;18,19,20;21,22,23];
for k=a
s=s+k;
end
disp(s');

这里是一行一行累加的。

4.3.4while语句

while语句的一般格式为：

其执行过程为：若条件成立，则执行循环体语句，执行后再判断条件是否成立，如果不成立则跳出循环。

break：跳出整个循环

continue：跳出当前循环

例四：

从键盘输入若干个数，当输入0时结束输入，求这些数的平均值和它们之和。

>> sum=0;
cnt=0;
val=input('Enter a number (end in 0):');
while (val~=0)
sum=sum+val;
cnt=cnt+1;
val=input('Enter a number (end in 0):');
end
if (cnt > 0)
sum
mean=sum/cnt
end

求[100，200]之间第一个能被21整除的整数。

>> for n=100:200
if rem(n,21)~=0
continue
end
break
end
n

4.3.5循环的嵌套

若一个数等于它的各个真因子之和，则称该数为完数，如6=1+2+3，所以6是完数。求[1,500]之间的全部完数。

for m=1:500
    s=0;
    for k=1:m/2
        if rem(m,k)==0
            s=s+k;
        end
    end
    if m==s
        disp(m);
    end
end

4.4极限

(1) limit(f,x,a)：计算当变量x趋近于常数a时，f(x)函数的极限值；
(2) limit(f,x,a,‘right’)：‘right’表示变量x从右边趋近于a；
(3) limit(f,x,a,‘left’)： ‘left’表示变量x从左边趋近于a

注：正无穷，则可以用+inf

例：

syms x; %定义变量x
limit(1/x^2-cot(x)^2,x,0) 
ans=2/3

syms a,b,x;
limit((sin(a/x^2)+cos(b/x))^(x^2),x,inf)
ans=exp(a-1/2*b^2)

syms x;
limit(x^x,x,0,'right')
ans=1

syms t,x;
limit((1+2*t/x)^(3*x),x,inf)
ans = exp(6*t)

4.5代数方程(组)的解

1. roots§：这是求多项式根的命令，其中p是多项式的系数，按降幂方式排列
2. fzero(f,x0): 在x0的附近寻找函数f的近似零点
3. solve(f,x)：求解表达式f的代数方程，求解变量为x
4. solve(f1,f2,…,fn,x1,x2,…,xn)：求解符号表达式f1,f2,…,fn组成的代数方程组，求解变量分别是x1,x2,…xn。

syms x;
f='exp(x)-x-3'; %定义函数f
fzero(f,[1,2])
ans =1.5052

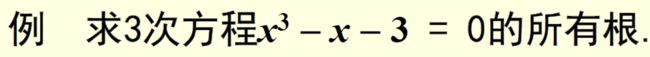
roots([1,0,-1,-3])
ans =
1.6717
-0.8358 + 1.0469i
-0.8358 - 1.0469i

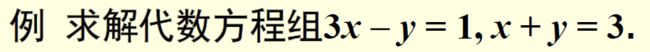
[a,b]=solve('3*x-y=1','x+y=3','x,y')

4.6导数

diff(f,x)：以x为自变量，对符号表达式f求一阶导数；

diff(f,x,n)：以x为自变量，对符号表达式f求n阶导数。

syms x;
y='x*exp(3*x)';
y1=diff(str2sym(y),x); % 1阶导数
y5=diff(str2sym(y),x,5); % 5阶导数
y1,y5

syms x
y=log(x+sqrt(1+x^2));
y1=diff(y,x); % 1阶导数
y2=diff(y,x,2); % 2阶导数
simplify(y1),simplify(y2)%结果化简

ans =1/(1+x^2)^(1/2)
ans =-x/(1+x^2)^(3/2)

这里需要留意：新版本化简用simplify函数

4.7函数极值

(1) fminbnd(f,x1,x2)——求函数f在区间[x1,x2]上的极小值；

(2) fminsearch(‘f’,x0)——求多元函数f在x0附近的极小值

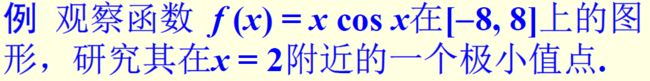
画图：

syms x;
f='x*cos(x)'; %定义函数f
fplot(f,[-8,8])
grid; %显示网格

用fminbnd函数求极小值：

[X,FVAL] = fminbnd(f,-8,8)
X = 3.4256
FVAL = -3.2884
[X,FVAL] = fminbnd(f,-8,0)
X = -6.4373
FVAL = -6.3610
[X,FVAL] = fminbnd(f,-4,0)
X = -0.8603
FVAL = -0.5611

用fminsearch函数求极小值：

[X,FVAL] = fminsearch (f,2)
X = 3.4256
FVAL = -3.2884
[X,FVAL] = fminsearch (f,-4)
X = -6.4373
FVAL = -6.3610
[X,FVAL] = fminsearch (f,-2)
X = -0.8603
FVAL = -0.5611

4.8积分的计算

int(f,x)：以x为自变量，对被积函数或符号表达式f求不定积分；
int(f,x,a,b)：求定积分运算。a,b分别表示定积分的下限和上限。该函数求被积函数在区间[a,b]上的定积分。

syms x s; % 表明x ,s为符号变量
f=sin(2*x)+s^2; % 定义符号表达式
int(f,x) % 对变量x求不定积分

注意：在所求结果后加常数运行结果如下：
$$ans=-1/2\ast cos(2\ast x)+s^2\ast x$$

syms x s; % 表明x ,s为符号变量
f=sin(2*x)+s^2; % 定义符号表达式
int(f,x, -pi/2,pi/2) % 对变量x求定积分，
ans = s^2*pi

4.9微分方程求解

Dy表示y’ ;
D2y表示y ’ ‘;
Dy(0)=5表示y’ (0)=5

dsolve(‘f’,’c’,’v’)：这个命令包括三部分，微分方程，初始条件，指定变量。

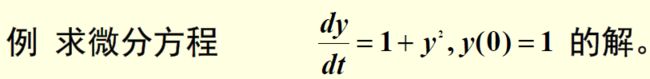
dsolve(‘Dy=1+y^2’) % 求一阶方程的通解
ans =tan(t+C1) % C1为积分常数。
dsolve('Dy=1+y^2', 'y(0)=1') % 求特解
ans =tan(t+1/4*pi)

4.10线性代数运算

1. 矩阵的转置
   转置运算符是单撇号(’)。

2. 矩阵的旋转
   利用函数rot90(A,k)将矩阵A旋转90º的k倍，当k为1时可省略。

3. 矩阵的左右翻转
   对矩阵实施左右翻转是将原矩阵的第一列和最后一列调换，第二列和倒数第二列调换，…，依次类推。MATLAB对矩阵A实施左右翻转的函数是fliplr(A)。

4. 矩阵的上下翻转
   MATLAB对矩阵A实施上下翻转的函数是flipud(A)。

5. 矩阵的逆
   对于一个方阵A，如果存在一个与其同阶的方阵B，使得：A·B=B·A=I (I为单位矩阵)则称B为A的逆矩阵，当然，A也是B的逆矩阵。
   求一个矩阵的逆是一件非常烦琐的工作，容易出错，但在MATLAB中，求一个矩阵的逆非常容易。
   求方阵A的逆矩阵可调用函数inv(A)。

6. 方阵的行列式
   把一个方阵看作一个行列式，并对其按行列式的规则求值，这个值就称为矩阵所对应的行列式的值。
   在MATLAB中，求方阵A所对应的行列式的值的函数是det(A)。

7. 矩阵的秩与迹
   1）矩阵的秩
   矩阵线性无关的行数与列数称为矩阵的秩。在MATLAB中，求矩阵秩的函数是rank(A)。
   2） 矩阵的迹
   矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。在MATLAB 中，求矩阵的迹的函数是trace(A)。

8. 矩阵的特征值与特征向量
   在MATLAB中，计算矩阵A 的特征值和特征向量的函数是eig(A)，常用的调用格式有3种：

   (1) E=eig(A)：求矩阵A 的全部特征值，构成向量E。
   (2) [V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。
   (3) [V,D]=eig(A,‘nobalance’)：与第2种格式类似，但第2种格式中先对A作相似变换后求矩阵A的特征值和特征向量，而格式3直接求矩阵A的特征值和特征向量。

编程训练

分段函数

根据我国个人所得税计算方法,编制程序,要求:使用者在系统提示下通过键盘输入月工资薪金收入总数,计算机则在屏幕上显示个人所得税额,界面友好,方便使用

个人所得税计算方法:
月个人所得税＝（月工资薪金收入－2000）*适用税率－速算扣除数
附表：个人所得税税率表（工资、薪金所得适用）

	全月应纳税所得额	税率（％）	速算扣除数
1	不超过500元的	5％	0
2	超过500元至2000元的部分	10％	25
3	超过2000元至5000元的部分	15％	125
4	超过5000元至20000元的部分	20％	375
5	超过20000元至40000元的部分	25％	1375
6	超过40000元至60000元的部分	30％	3375
7	超过60000元至80000元的部分	35％	6375
8	超过80000元至100000元的部分	40％	10375
9	超过100000元的部分	45％	15375

编写Matlab命令文件：

wages=input('请输入您的工资：');
wage=wages-2000;
if(wage<=0)
    tax=0;
elseif(wage<=500)
    tax=wage*0.05;
elseif(wage<=2000)
    tax=500*0.05+(wage-500)*0.1-25;
elseif(wage<=5000)
    tax=500*0.05+1500*0.1+(wage-2000)*0.15-25-125;
elseif(wage<=20000)
    tax=500*0.05+1500*0.1+3000*0.15+(wage-5000)*0.2-25-125-375;
elseif(wage<=40000)
    tax=500*0.05+1500*0.1+3000*0.15+15000*0.2+(wage-20000)*0.25-25-125-375-1375;
elseif(wage<=60000)
    tax=500*0.05+1500*0.1+3000*0.15+15000*0.2+20000*0.25+(wage-40000)*0.3-25-125-375-1375-3375;
elseif(wage<=80000)
    tax=500*0.05+1500*0.1+3000*0.15+15000*0.2+20000*0.25+20000*0.3+(wage-60000)*0.35-25-125-375-1375-3375-6375;
elseif(wage<=100000)
    tax=500*0.05+1500*0.1+3000*0.15+15000*0.2+20000*0.25+20000*0.3+20000*0.35+(wage-80000)*0.4-25-125-375-1375-3375-6375-10375;
else
    tax=500*0.05+1500*0.1+3000*0.15+15000*0.2+20000*0.25+20000*0.3+20000*0.35+20000*0.4+(wage-100000)*0.45-25-125-375-1375-3375-6375-10375-15375;
end
tax

素数

求［2，999］中同时满足下列条件的数
（１）该数各位数字之和为奇数
（２）该数是素数

for i=2:999
    a=rem(i,10);
    b=rem(fix(i/10),10);
    c=fix(i/100);
    if (rem((a+b+c),2)~=0)&(isprime(i)==1)%isprime判断素数
        disp(i);
    end
end

运行结果得出以下的数：
3 5 7 23 29 41 43 47 61 67 83 89 113 131 137 139 151 157 173 179 191
193 197 199 223 227 229 241 263 269 281 283 311 313 317 331 337 353
359 373 379 397 401 409 421 443 449 461 463 467 487 557 571 577 593
599 601 607 641 643 647 661 683 719 733 739 751 757 773 797 809 821
823 827 829 863 881 883 887 911 919 937 953 971 977 991 997

水仙花数

水仙花数是指一个3位自然数，其各位数字的立方和等于该数本身，输出1000以内的水仙花数，并求其个数。

y=[];%空矩阵
count=0;
for i=100:999
    a=rem(i,10);
    b=rem(fix(i/10),10);
    c=fix(i/100);
    if(a^3+b^3+c^3==i)
        y=[y,i];%不断扩充
        count=count+1;
    end
end
y,count

突变素数

当一个素数（只有两个正因数（1和自己）的自然数即为素数）与其前一个素数的差值大于等于5时，将其称之为“突变素数”(2不是“突变素数”)，求10000以内的“突变素数”的个数.

y=[];
k=0;
count=0;
for i=1:10000
    if isprime(i)==1
        if (i-k)>=5 
            y=[y,i];
            count=count+1;
        end
        k=i;
    end
end
y,count

结果：count=820

方差分析1

试验3种猪饲料的饲养效果，得到9头猪的增重(单位：kg)如下：

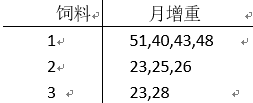
用MATLAB编程做作方差分析，估计各个总体的未知参数μi和μ。（不允许用anova1工具箱）

先用SAS得到结果方便后面检验：

data ex;
do a=1 to 3;input n@@;
do i=1 to n;input x@@;
output;end;end;
cards;
4 51 40 43 48   
3 23 25 26       
2 23 28 
;
proc anova data=ex;class a;model x=a;
run;

SST——(每个因素的均值-总均值)^2的和
SSA——每个水平的个数*(每个水平的均值-总均值)^2的和
SSE=SST-SSA
F=(SSA/(R-1))/(SSE/(n-R)) R为水平个数

a1=[51,40,43,48];
a2=[23,25,26];
a3=[23,28];
a=[a1,a2,a3];n=length(a);
b=[1 1 1 1 2 2 2 3 3];
sst=0;
for i=1:n
    sst=sst+(a(i)-mean(a))^2;
end
ssa=0;
for i=1:3
    an=a(b==i);num=length(an);
    ssa=ssa+num*(mean(an)-mean(a))^2;
end
sse=sst-ssa;
f=(ssa/2)/(sse/(n-3));
p=1-fcdf(f,2,n-3);
ssa,sse,sst,f,p

可以看出和SAS所得结果一样

方差分析2

测定4种种植密度下金皇后玉米的千粒重(单位：g)如下：

用MATLAB编程做作方差分析，估计各个总体的未知参数mI和μ。（不允许用anova1工具箱）

首先还是用SAS做出结果方便检验：

data ex;
do a=1 to 4;input n@@;
do i=1 to n;input x@@;
output;end;end;
cards;
4 247 258 256 251
4 238 244 246 236
4 214 227 221 218
4 210 204 200 210
;
proc anova data=ex;class a;model x=a;
run;

编写Matlab代码：

a=[247,258,256,251
238,244,246,236
214,227,221,218
210,204,200,210];
[m,n]=size(a);
sst=0;
for i=1:m
    for j=1:n
        sst=sst+(a(i,j)-mean(a(:)))^2;
    end
end
ssa=0;
for i=1:m
    for j=1:n
        ssa=ssa+(mean(a(i,:))-mean(a(:)))^2;
    end
end
sse=0;
for i=1:m
    for j=1:n
        sse=sse+(a(i,j)-mean(a(i,:)))^2;
    end
end
f=(ssa/m-1)/(sse/(m*n-n));
p=1-fcdf(f,m-1,m*n-n);
ssa,sse,sst,f,p

和SAS所得结果一样

主成分分析

下表是某地区某时间的气候综合指数，其中，x1为某地区平均降水量，x2为气压值，x3为气温值，x4为绝对湿度。试用主成分分析法分析该地区的气候综合指数。

x1	42.4	10.2	116.8	4.8	43.6	13.3	61.1	99.3	139.3	55.5	68.3
x2	12	19.4	24.6	28.8	24.7	28.3	18.7	18.3	9.4	8.1	3.5
x3	24	18.4	12.5	1	2.8	1.8	8.8	13.7	18.7	22.6	26.7
x4	22.7	15.1	12.1	4.4	5.4	4.7	8.5	11.8	17.9	22.3	29.1
x1	83.4	90	18.8	47.6	99.6	100.1	80.6	90	100.8	146.1	55.1
x2	5.7	12.8	19.4	22.8	21	23	2.8	21.2	15.1	8.4	6.7
x3	27.5	23.7	17.4	13.3	9.5	3.6	2.6	6.8	14.2	19.6	22.4
x4	29.4	23.6	15.1	12.3	10.6	6.7	6.2	8.3	13.7	18.6	21.2

主成分分析的一般步骤

（1）将观测数据标准化，并计算及。

（2）由相关系数矩阵****

（3）得到特征值及各个主成分的方差贡献率、贡献率和累计贡献率，并根据累计贡献率确定主成分保留的个数。

（4）写出个基本方程组：

其中，。

利用施密特正交方法，对每一个求它的对应基本方程组的解，然后令,从而得到用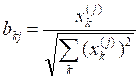所表示的主成分向量，或将代入后得到用所表示的主成分向量。

（5）将的观测值代入主成分向量的表达式中计算各个主成分向量。

（6）计算原指标与主成分的相关系数即因子载荷，解释主成分的意义。

请按照以上算法步骤编写MATLAB程序，不允许用princomp工具箱

+++

解：

由于数据较多，我们将数据写入excel表格并放入工作路径中，通过读取得到数据

x=xlsread('jy.xlsx','Sheet1','B1:W4');%读取表格中数据
x=x';
xx=zscore(x);%标准化
R=corrcoef(xx);%求相关系数矩阵
[v,d]=eig(R);%d-特征值，v-特征值对应的特征向量
lamda=diag(d);%将特征值抽取出来
gx=lamda/sum(lamda);%计算贡献比例
gx=sort(gx,'descend');%倒序排序，根据计算发现留下两个主成分
zcf=[v(:,4),v(:,3)];%将第一主成分和第二主成分特征向量抽取出来
defen=xx*zcf;%算出主成分得分
zhpj=defen*gx(1:2,:);%综合评价=得分*贡献率

第四问：
$$z1=0.2320\ast x1-0.5301\ast x2+0.5711\ast x3+0.5823\ast x4$$

$$z2=-0.9347\ast x1+0.1105\ast x2+0.2465\ast x3+0.2312\ast x4$$

综合评价

以下是某种算法

（１）确定因素集；

（２）确定评判集；

（３）进行单因素评判得；

（４）构造综合评判矩阵

（５）综合评判：对于权重A={a1,a2,,an}，计算，并根据最大隶属度原则作出评判．

在进行综合评判时，根据算子的不同定义，可以得到不同的模型．

请用MATLAB编写上面程序，并计算下面的问题。

考虑一个服装评判的问题，为此建立因素集，其中u1表示花色，u2表示式样，u3表示耐穿程度，u4表示价格．建立评判集，其中v1表示很欢迎，v2表示较欢迎，v3表示不太欢迎，v4表示不欢迎．进行单因素评判的结果如下：

，，

，．

设有两类顾客，他们根据自己的喜好对各因素所分配的权重分别为：

．

试分析这两类顾客对此服装的喜好程度．

+++

解：

1、因素集确定：根据题目要求，设u1 表示花色，u2 表示式样，u3 表示耐穿程度，u4 表示价格，则得到因素集为：

2、评判集确定：为了更好的对所有的因素做出评价，则设以下以下4 个程度：其中v1 表示很欢迎，v2 表示较欢迎，v3 表示不太欢迎，v4 表示不欢迎，由以上得到评判集：

3、单因素评判：对花色、式样、耐穿程度、价格4 种进行单因素评判得到以下结果：

4、构造评价矩阵：根据以上4 种单因素评判得到的结果，得到评价矩阵：

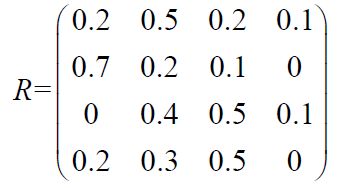
5、综合评判：

为了同时兼顾到所有因素对整体喜好程度的影响，则需要建立加权平均模型。

B = A* R = (b1,b2 ,b2 ,b4 )

根据以上模型在MATLAB 中编程：

r=[0.2,0.5,0.2,0.1
0.7,0.2,0.1,0
0,0.4,0.5,0.1
0.2,0.3,0.5,0];
a=[0.1,0.2,0.3,0.4
0.4,0.35,0.15,0.1];
B=a*r

根据最大隶属原则可以得到，A1类顾客对产品的喜好程度为不太欢迎，A2类顾客对产品的喜好程度为比较欢迎。

结语

芜湖，终于赶在忍界大战前写完了！今晚第三次忍界大战！应该比春晚好看多了

上场名单
TES 36鲛 宇智波卡萨 大手丸 宇智波水 药师预
IG 迈特晒 旋涡宁人 卡卡鸡 佐芙 春野蓝

大伙们今晚把饭盆收一收，该减减肥了(lll￢ω￢)