核函数(Kernels)
引言:核函数或核方法是将低维度数据映射成高维度特征的高效工具,它不仅帮助我们完成部分线性不可分问题的处理,同时计算的时间复杂度依然保持在低维度(即效率很高)。
1.核函数简述
以房屋建筑面积作为输入x的问题为例,我们可以构建一个x,x^2,x^3组成的三次方方程。为了区别两组不同的变量,我们称原始输入值x为问题的输入元素。当通过学习算法映射为一组新的数值后,我们称新的数值[x,x^2,x^3]^T为输入特征。将\phi称为特征映射。在当前的例子中可写作:
\phi(x)= \begin{bmatrix} x\\ x^2\\ x^3 \end{bmatrix} \qquad\qquad\qquad(1)
相比于输入元素x我们更愿意将特征\phi(x)应用于支持向量机算法中。要完成这一切很简单,我们只需将算法中所有的x替换成\phi(x)即可。
因为算法可以仅用\langle x,z\rangle内积的形式表示,我们可以将所有的内积替换成\langle\phi(x),\phi(z)\rangle。对于给定的输入特征\phi(x),对应的核函数定义为:
K(x,z) = \langle\phi(x),\phi(z)\rangle = \phi(x)^T\phi(z)
由上式可知,确定特征映射\phi后,我们可以通过求解\phi(x)和\phi(z)和它们的内积很轻松地计算出K(x,z)。但有趣的是,有时特征向量\phi(x)的计算量很大(特征映射可能是一个高阶的向量),但K(x,z)却很容易求解。在这种情况下,我们直接计算K(x,z),将SVM算法映射到高维度空间,不去求解具体的特征向量\phi(x)。
2.核函数示例
下面举一个例子。对于x,z\in\Bbb R^n,有:
K(x,z) = (x^Tz)^2.
将上式展开:
\begin{align} K(x,z) &= \left(\sum_{i=1}^nx_iz_i\right)\left(\sum_{j=1}^nx_jz_j\right)\\ &=\sum_{i=1}^n\sum_{j=1}^nx_ix_jz_iz_j\\ &=\sum_{i,j=1}^n(x_ix_j)(z_iz_j) \end{align}
又K(x,z) = \phi(x)^T\phi(z),则n=3时对应的特征映射\phi为:
\phi(x)= \begin{bmatrix} x_1x_1\\ x_1x_2\\ x_1x_3\\ x_2x_1\\ x_2x_2\\ x_2x_3\\ x_3x_1\\ x_3x_2\\ x_3x_3\\ \end{bmatrix}.
注意计算高维度向量\phi(x)需要O(n^2)的时间,但计算K(x,z)(即(x^Tz)^2)仅需要O(n)的时间——和计算输入属性的时间一致。
我们将上面的核函数再更改一下,有:
\begin{align} K(x,z) &= (x^Tz+c)^2\\ &=\sum_{i=1}^n\sum_{j=1}^nx_ix_jz_iz_j\\ &=\sum_{i,j=1}^n(x_ix_j)(z_iz_j)+\sum_{i=1}^n(\sqrt{2c}x_i)(\sqrt{2c}z_i)+c^2.\\ \end{align}
这个模型对应的映射(依然假设n=3):
\phi(x)= \begin{bmatrix} x_1x_1\\ x_1x_2\\ x_1x_3\\ x_2x_1\\ x_2x_2\\ x_2x_3\\ x_3x_1\\ x_3x_2\\ x_3x_3\\ \sqrt{2c}x_1\\ \sqrt{2c}x_2\\ \sqrt{2c}x_3\\ c\\ \end{bmatrix}.
参数c控制x_i(一阶)与x_ix_j(二阶)之间的相关权重。
更进一步来看,K(x,z)对应到{n+d \choose d}维特征空间的特征映射,其对应的所有单项式x_{i_1}x_{i_2}\ldots x_{i_k},最多至阶数d。然而尽管工作在O(n^d)的维度空间,计算K(x,z)依然只需要O(n)的时间,因此求解问题时,我们不去求解具体的输入特征。
3.核函数的理解
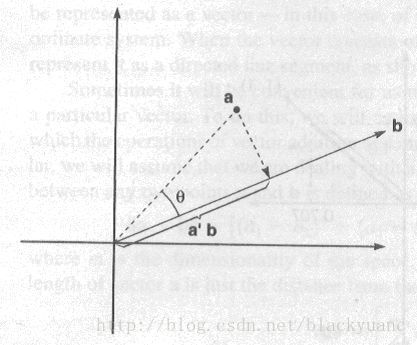
用几何方法直观地理解一下核函数,显然当\phi(x)与\phi(z)很接近时,我们预计K(x,z)=\phi(x)^T\phi(z)将会很大;相反地,当\phi(x)与\phi(z)相差很大甚至相互垂直,那么K(x,z)就会很小。所以我们可以将核看成\phi(x)与\phi(z)或x与z相似度的度量。
根据这一观点,当你在研究某一学习问题,你就需要找到一个核函数K(x,z)能够准确地描述x与z之间的相似度。假设你选择下面这个核函数:
K(x,z)=exp\left(-\frac{\Vert x-z\Vert^2}{2\sigma^2}\right).
这是一个x与z相似度的可靠描述吗?当x与z接近时函数值接近于1,当x与z相差很远时函数值接近于0。我们可以将这个核函数应用于SVM吗?对于这个函数,结果是肯定的(这个核函数称为高斯核,对应一个无穷维的特征映射)。
那么问题来了,对于任意一个核函数我们如何知道它是否是一个有效的核函数,即是否存在一个映射\phi使得K(x,z)=\phi(x)^T\phi(z)对于任意x,z均成立。要解决这个问题,我们就需要后面的Mercer定理。
4.核函数的有效条件
Mercer定理:
给定K:\Bbb{R}^n\times\Bbb{R}^n\to\Bbb{R},要使K为有效核,对于任意\{x^{(1)},x^{()},\ldots ,x^{(m)}\}(m\lt\infty),对应的核矩阵必是对称半正定矩阵。
证明:
假设有一个有效的核函数K,同时有一个包含m个样本的训练集\{x^{(1)},x^{(2)},\ldots ,x^{(m)}\}。我们定义一个m\times m的矩阵K,其中K_{ij}=K(x^{(i)},x^{(j)}),我们将这个矩阵称为核矩阵。则有:
\begin{align} K_{ij}&=K(x^{(i)},x^{(j)})=\phi(x^{(i)})^T\phi(x^{(j)})=\langle \phi (x^{(i)}),\phi(x^{(j)})\rangle\\ &=\langle \phi (x^{(j)}),\phi(x^{(i)})\rangle=\phi(x^{(j)})^T\phi(x^{(i)})=K(x^{(j)},x^{(i)})\\ &=K_{ji} \end{align}
由上式的证明可知,K矩阵一定是对称矩阵。接下来我们用\phi_k(x)表示向量\phi(x)的第k个元素,对于任意一个m维向量z有:
\begin{align} z^TKz &=\sum_i\sum_jz_iK_{ij}z_j\\ &=\sum_i\sum_jz_i\phi(x^{(i)})\phi(x^{(j)})z_j\\ &=\sum_i\sum_jz_i\sum_k\phi_k(x^{(i)})\phi_k(x^{(j)})z_j\\ &=\sum_k\sum_i\sum_jz_i\phi_k(x^{(i)})\phi_k(x^{(j)})z_j\\ &=\sum_k\left(\sum_iz_i\phi_k(x^{(i)})\right)^2\\ &\ge0 \end{align}
由z是任意的,我们可知K一个是个半正定矩阵。所以对于任何一个有效的核函数K,其对应生成的核矩阵是一个对称半正定矩阵。我们上面证明了命题的必要性,实际上这也是一个充分条件。