用CUDA求解矩阵的逆,有多种方法,也可以自己编写内核函数去实现,我查阅CSDN上用
cublas求解矩阵逆的方法,但是作者写的比较繁琐,其他观看学习的人会觉得比难懂。所以我
决定自己写一个。我采用的是LU分解法,cublas提供了相应的函数。代码如下:
#include
#include
#include
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include
#define cudacall(call) \
do \
{ \
cudaError_t err = (call); \
if(cudaSuccess != err) \
{ \
fprintf(stderr,"CUDA Error:\nFile = %s\nLine = %d\nReason = %s\n", __FILE__, __LINE__, cudaGetErrorString(err)); \
cudaDeviceReset(); \
exit(EXIT_FAILURE); \
} \
} \
while (0)
#define cublascall(call) \
do \
{ \
cublasStatus_t status = (call); \
if(CUBLAS_STATUS_SUCCESS != status) \
{ \
fprintf(stderr,"CUBLAS Error:\nFile = %s\nLine = %d\nCode = %d\n", __FILE__, __LINE__, status); \
cudaDeviceReset(); \
exit(EXIT_FAILURE); \
} \
\
} \
while(0)
void invert(float** src, float** dst, int n, const int batchSize)
{
cublasHandle_t handle;
cublascall(cublasCreate_v2(&handle));
int *P, *INFO;
cudacall(cudaMalloc(&P, n * batchSize * sizeof(int)));
cudacall(cudaMalloc(&INFO, batchSize * sizeof(int)));
int lda = n;
float **A = (float **)malloc(batchSize * sizeof(float *));
float **A_d, *A_dflat;
cudacall(cudaMalloc(&A_d, batchSize * sizeof(float *)));
cudacall(cudaMalloc(&A_dflat, n*n*batchSize * sizeof(float)));
A[0] = A_dflat;
for (int i = 1; i < batchSize; i++)
A[i] = A[i - 1] + (n*n);
cudacall(cudaMemcpy(A_d, A, batchSize * sizeof(float *), cudaMemcpyHostToDevice));
for (int i = 0; i < batchSize; i++)
cudacall(cudaMemcpy(A_dflat + (i*n*n), src[i], n*n * sizeof(float), cudaMemcpyHostToDevice));
cublascall(cublasSgetrfBatched(handle, n, A_d, lda, P, INFO, batchSize));
int *INFOh=new int[batchSize];
//int INFOh[batchSize];
cudacall(cudaMemcpy(INFOh, INFO, batchSize * sizeof(int), cudaMemcpyDeviceToHost));
for (int i = 0; i < batchSize; i++)
if (INFOh[i] != 0)
{
fprintf(stderr, "Factorization of matrix %d Failed: Matrix may be singular\n", i);
cudaDeviceReset();
exit(EXIT_FAILURE);
}
float **C = (float **)malloc(batchSize * sizeof(float *));
float **C_d, *C_dflat;
cudacall(cudaMalloc(&C_d, batchSize * sizeof(float *)));
cudacall(cudaMalloc(&C_dflat, n*n*batchSize * sizeof(float)));
C[0] = C_dflat;
for (int i = 1; i < batchSize; i++)
C[i] = C[i - 1] + (n*n);
cudacall(cudaMemcpy(C_d, C, batchSize * sizeof(float *), cudaMemcpyHostToDevice));
cublascall(cublasSgetriBatched(handle, n, (const float **)A_d, lda, P, C_d, lda, INFO, batchSize));
cudacall(cudaMemcpy(INFOh, INFO, batchSize * sizeof(int), cudaMemcpyDeviceToHost));
for (int i = 0; i < batchSize; i++)
if (INFOh[i] != 0)
{
fprintf(stderr, "Inversion of matrix %d Failed: Matrix may be singular\n", i);
cudaDeviceReset();
exit(EXIT_FAILURE);
}
for (int i = 0; i < batchSize; i++)
cudacall(cudaMemcpy(dst[i], C_dflat + (i*n*n), n*n * sizeof(float), cudaMemcpyDeviceToHost));
cudaFree(A_d); cudaFree(A_dflat); free(A);
cudaFree(C_d); cudaFree(C_dflat); free(C);
cudaFree(P); cudaFree(INFO); cublasDestroy_v2(handle); delete[]INFOh;
}
void test_invert()
{
const int n = 3;
const int mybatch = 4;
//Random matrix with full pivots
float full_pivot[n*n] = { 0.5, 3, 4,
1, 3, 10,
4 , 9, 16 };
//Almost same as above matrix with first pivot zero
float zero_pivot[n*n] = { 0, 3, 4,
1, 3, 10,
4 , 9, 16 };
float another_zero_pivot[n*n] = { 0, 3, 4,
1, 5, 6,
9, 8, 2 };
float another_full_pivot[n * n] = { 22, 3, 4,
1, 5, 6,
9, 8, 2 };
float *result_flat = (float *)malloc(mybatch*n*n * sizeof(float));
float **results = (float **)malloc(mybatch * sizeof(float *));
for (int i = 0; i < mybatch; i++)
results[i] = result_flat + (i*n*n);
float **inputs = (float **)malloc(mybatch * sizeof(float *));
inputs[0] = zero_pivot;
inputs[1] = full_pivot;
inputs[2] = another_zero_pivot;
inputs[3] = another_full_pivot;
for (int qq = 0; qq < mybatch; qq++) {
fprintf(stdout, "Input %d:\n\n", qq);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
fprintf(stdout, "%f\t", inputs[qq][i*n + j]);
fprintf(stdout, "\n");
}
}
fprintf(stdout, "\n\n");
invert(inputs, results, n, mybatch);
for (int qq = 0; qq < mybatch; qq++) {
fprintf(stdout, "Inverse %d:\n\n", qq);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
fprintf(stdout, "%f\t", results[qq][i*n + j]);
fprintf(stdout, "\n");
}
}
}
int main(void) {
test_invert();
return 0;
}
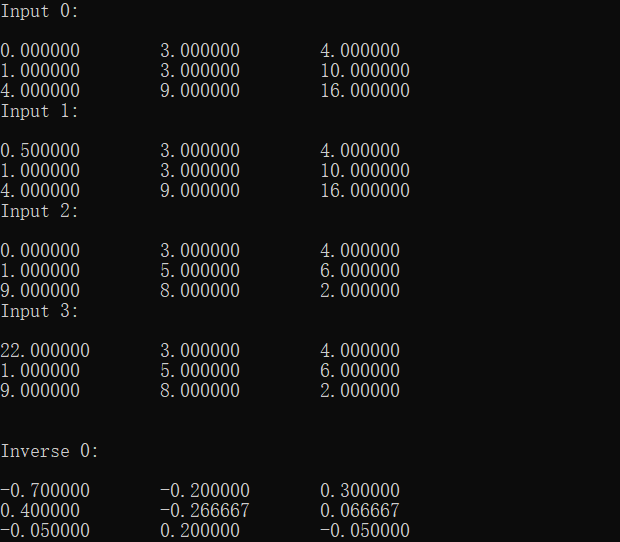
运行结果: