均分纸牌(线性、环形、二维)

感觉好久没写博客了…

---

题目描述

有N堆纸牌，编号分别为1,2,…,N。每堆上有若干张，但纸牌总数必为N的倍数。可以在任一堆上取若干张纸牌，然后移动。

移牌规则为：在编号为1堆上取的纸牌，只能移到编号为2的堆上；在编号为N的堆上取的纸牌，只能移到编号为N-1的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。

现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

例如N=4，4堆纸牌数分别为：
①9 ②8 ③17 ④6
移动3次可达到目的：
从 ③ 取4张牌放到 ④ （9,8,13,10）
从 ③ 取3张牌放到 ②（9,11,10,10）
从 ② 取1张牌放到①（10,10,10,10）。

---

思路

这一题还是比较容易的，考虑到第一堆只能给第二堆若干张或者由第二堆给第一堆若干张。
所以当确定了第一堆的状态后，第二堆就变成了新的第一堆。按照上面的思想依次考虑即可;

所以代码也不难写，只需要从第一堆开始判断拥有的牌数是不是平均值，如果是均值则跳过，如果不是则需要的移动次数加1;

时间复杂度为O(n)；
点此交题：均分纸牌

参考代码

#include 
using namespace std;

int main()
{
    int n, ans = 0, ave, cnt = 0;
    cin >> n;
    vector<int> a(n + 1), sum(n + 1);
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        cnt += a[i];
    }
    ave = cnt / n;
    sum[0] = 0;
    for(int i = 1; i <= n; i++)
    {
        sum[i] = sum[i - 1] + a[i] - ave;
        if(sum[i])
            ans++;
    }
    cout << ans << endl;

    return 0;
}

---

PS:稍微偏偏题；这样的思路可以很快的的解决一些区间类的问题。例如：

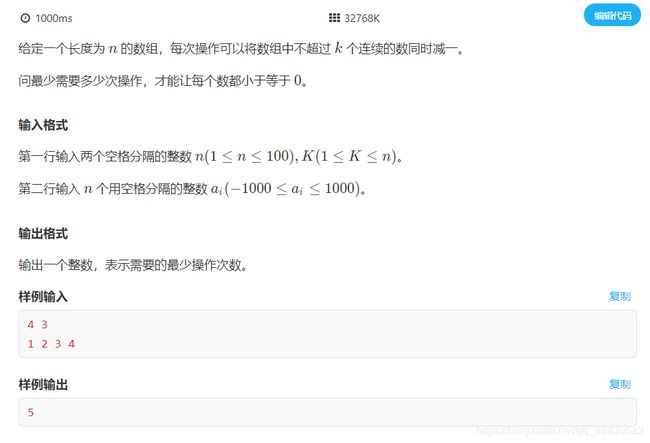
说实话，这题我思考了好久都没有好的做法(可能是太蠢了…
正解是你考虑最左边的元素只能选取(1 ~ k)这一段进行减操作，所以对1进行的减操作就是a[1]次，然后依次考虑第2位、第3位是否满足 <=0, 若满足则跳过 不满足则对区间 (i ~ i + k)进行 减 a[i]操作即可；
也是O(n)的复杂度;代码就大家自己实现一下吧;

OK,回到正题，上面我们所说的就是简单的线性的均分纸牌问题；接下来我们说说环形的均分纸牌问题；

---

题目描述

还是刚才的问题，只不过是刚才是线性的，现在变成了一个环； 即第一个人可以将自己的牌给最后一个人，也可以从最后一个人哪里拿牌； 最后一个人同理； 询问这个时候需要的最小代价；

PS：稍稍有点不同是上面那题询问的是最少的操作次数，这道题问的是最小的代价(挪动一张牌的代价为1);

若刚才那题改为求最小代价的话，思路还是一样的，因为第一堆只能由第二堆（获得或给予）得到均值；

考虑一下如果是环形改为求最小移动次数又该咋样做呢？

---

思路

OK,我们如何解决这道看似很难得题目呢？

我们在做环形的题目时候有种经常使用的解法是将环形拆分为线形；(如：环形的石子合并，环形的打家劫舍…)
此题当然也可以将环形拆分为线形； 有一个结论是 在均分纸牌的过程中，肯定有一个人是不参与的(躺赢Orz 因为当其他n - 1都处于均值是，则第n个人必定处于均值； 至于为啥？ 你可以问问神奇的海螺(逃.

OK,那我们可以枚举一下那一项不进行参与，然后从这个点将环断开；(这里不理解的，可以考虑上一题最后一个人就是躺赢的，他啥都没做就满足条件了)。然后O(n)扫出此时的最小代价； 然后维护一个最小代价即可;
时间复杂度是O(n*n)的； 然鹅

---

这题的数据范围是1000000,时限是1000ms。 n方复杂度肯定会超时的；那我们如何优化呢？
我们可以先对每一堆牌减去均值。 然后求出一个前缀和；
试想，假如sum[i] = 0, 那是不是代表着 前 i - 1项可以通过某种方式使得前i - 1项都处于均值呢？ 答案是肯定的。 所以 我们最后只需要得到 所有前缀和绝对值的和即可;

我们先来看看线性的均分纸牌，让我们对这个有个比较直观的认识;
假设 A数组存储的是减去均值后的纸牌个数。 S数组储存的是前缀和(减去均值的前缀和)

A[1] S[1]
A2 S2
A[3] S[3]
… …
A[n] S[n]

我们可以显然得到，当某个 S[i]不等于0时，那代表我 前 i - 1项肯定不能自给自足，还需要第i给贡献或者拿走一部分； 所以我们求出这样的一个前缀和， 然后对这个前缀和数组进行求绝对值的和就是线性的最小代价； 要求最小移动次数就是 S[i]不为0 则需要移动；

我们假设我们的断开点是k点
那么减去均值和得到的前缀和数组就是

A[k + 1] S[k + 1] - S[k]
A[k + 2] S[k + 2] - S[k]
A[k + 3] S[k + 3] - S[k]
… …
A[n] S[n] - S[k]
A[1] S1 + S[n] - S[k]
A2 S2 + S[n] - S[k]
… …
A[k] S[k] + S[n] - S[k]

考虑到最后一项 即现在的k是躺赢的人， 所以肯定有 S[k] + S[n] - S[k] = 0;
所以 S[n] = 0;
将式子中的S[n]替换为0，原式可以改写为:

A[k + 1] S[k + 1] - S[k]
A[k + 2] S[k + 2] - S[k]
A[k + 3] S[k + 3] - S[k]
… …
A[n] S[n] - S[k]
A[1] S1 - S[k]
A2 S2 - S[k]
… …
A[k] S[k] - S[k]

显然，这题变成了， 求一个数组中的点， 使得到达其他所有点的距离和最小的问题；(显然是中位数，至于为啥。
假设我们选择的点 左边有 a个点 右边有 b个点 a > b, 那么我们每向左移动一个单位，则距离和减少 a - b；当a < b 也是同理；
所以我们只有把选择的点选取为中位数的时候可以保证答案最优;

这道题也是一样的， 我们求出来的前缀和数组可以看做是上面的数组；

我们选取一个前缀和的中位数， 然后求一下当前点到其他点绝对值的和就是答案啦；

交题点此: 环形均分纸牌

参考代码

#include 
using namespace std;

#define MAX_N 1000010

int a[MAX_N], sum[MAX_N];

int main()
{
    int n;
    cin >> n;
    sum[0] = 0;
    long cnt = 0;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        cnt += a[i];
    }
    int age = cnt / n;
    for(int i = 1; i <= n; i++)
    {
        a[i] -= age;
        sum[i] = sum[i - 1] + a[i];
    }
    sort(sum + 1, sum + 1 + n);
    int mid = (n + 1) >> 1;
    long long ans = 0;
    for(int i = 1; i <= n; i++)
    {
        ans += abs(sum[i] - sum[mid]);
    }
    cout << ans << endl;
    return 0;
}

---

二维均分纸牌

有人看的话我在更新…