【机器学习实战】sklearn库中出现的线性模型(补充前篇线性回归)

线性模型

一般我们可以把线性模型写作： f(x)=wTx+b f ( x ) = w T x + b 的形式。sklearn中列举了线性回归、岭回归、lasso回归等线性模型，模型实在是多⊙▽⊙”，现将几个我印象比较深的做一下整理。
为了方便起见，我们令 wT=(w1,w2,...,wn,b) w T = ( w 1 , w 2 , . . . , w n , b ) ，因此预测值 f(x)=w1x1+w2x2+...+wnxn+b=wTx f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w n x n + b = w T x ，真实值为 y y ，样本数量为m个，即 (x1,x2,...,xm) ( x 1 , x 2 , . . . , x m ) ；特征为n个，即 (x1,x2,...,xn) ( x 1 , x 2 , . . . , x n ) 。

【线性回归】

线性回归采用的是最小二乘法的思想，即使所有预测值 f(x) f ( x ) 与其真实值 y y 的欧氏距离的平方最小， minw||wTx−y||2 min w | | w T x − y | | 2
其损失函数写为： L(w)=((∑i=1m|f(xi)−yi|2)12)2=∑i=1m(f(xi)−y)2 L ( w ) = ( ( ∑ i = 1 m | f ( x i ) − y i | 2 ) 1 2 ) 2 = ∑ i = 1 m ( f ( x i ) − y ) 2
有时为了方便求导会改写为 L(w)=12m∑i=1m(f(xi)−y)2 L ( w ) = 1 2 m ∑ i = 1 m ( f ( x i ) − y ) 2

【Ridge回归】

岭回归，其实就是在线性回归的最小二乘法基础上加了正则化项(有时也喜欢叫惩罚项)。
主要是因为最小二乘法采用的是无偏估计，它的无偏性导致其对病态数据会很敏感，比如出现了一个离所有数据都很远的数据，为了最小化所有数据到拟合模型的距离之和最小，我们的模型必然会偏向这个数据，这样我们的模型的拟合效果并不符合实际。(其实也就是过拟合现象，众所周知，我们常用正则化来处理过拟合现象)
因此，岭回归针对最小二乘法进行了改进，即 minw||wTx−y||2+λ||w||2 min w | | w T x − y | | 2 + λ | | w | | 2 ，观察这个公式我们可以发现 λ λ 越大，我们为了使 ||wTx−y||2+λ||w||2 | | w T x − y | | 2 + λ | | w | | 2 最小，必须使 w w 越小越好。
下图是 λ λ 和系数 w w 的关系，我们可以看出，当 λ λ 很大， w w 趋向于0；而当 λ λ 趋于0时，此时的系数 w w 趋于一般最小二乘法的解，系数会出现很大的振荡。因此我们有必要调整 λ λ ，保持这两者之间的平衡。(在官方库中 λ λ 是用 α α 表示的)

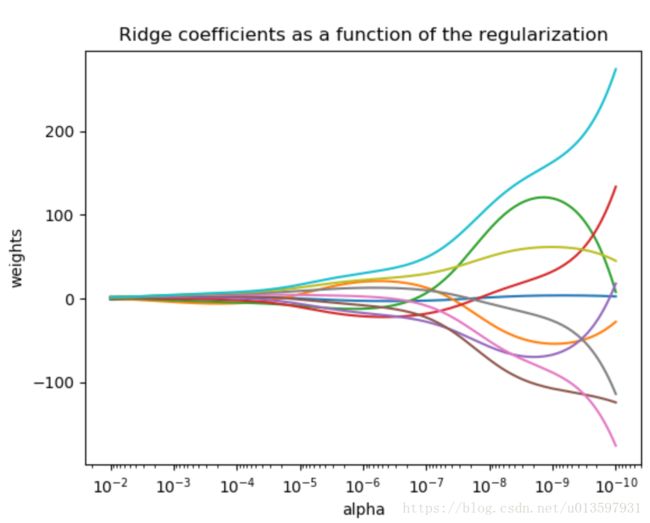
岭回归损失函数写为 L(w)=∑i=1m(f(xi)−y)2+λ∑j=1nw2j L ( w ) = ∑ i = 1 m ( f ( x i ) − y ) 2 + λ ∑ j = 1 n w j 2
为了方便求导会改写为 L(w)=12m∑i=1m(f(xi)−y)2+λ∑j=1nw2j L ( w ) = 1 2 m ∑ i = 1 m ( f ( x i ) − y ) 2 + λ ∑ j = 1 n w j 2

【Lasso回归】

emmm，Lasso回归和Ridge回归其实差不多嘛，主要区别在于正则化项Lasso回归用的是系数的L1范数(曼哈顿距离)，即 minw||wTx−y||2+λ||w|| min w | | w T x − y | | 2 + λ | | w | |
而Ridge回归用的是系数的L2范数(欧几里得距离)。
Lasso回归损失函数写为 L(w)=∑i=1m(f(xi)−y)2+λ∑j=1n|wj| L ( w ) = ∑ i = 1 m ( f ( x i ) − y ) 2 + λ ∑ j = 1 n | w j |
为了方便求导会改写为 L(w)=12m∑i=1m(f(xi)−y)2+λ∑j=1n|wj| L ( w ) = 1 2 m ∑ i = 1 m ( f ( x i ) − y ) 2 + λ ∑ j = 1 n | w j |

我们根据前一篇的线性回归练习，加上Lasso回归。

model_lasso=linear_model.Lasso(alpha=10)
model_lasso.fit(X_train,y_train)
print(model_lasso.coef_)     #系数，有些模型没有系数（如k近邻）
print(model_lasso.intercept_) #与y轴交点，即截距
y_lasso_pred = model_lasso.predict(X_test)
print("使用Lasso Regression模型的均方误差为:",metrics.mean_squared_error(y_test, y_lasso_pred))
print("使用Lasso Regression模型的均方根误差为:",np.sqrt(metrics.mean_squared_error(y_test, y_lasso_pred)))

输出为：
[ 0.0313973   0.         -0.         -0.72770526]
[ 31.34104409]
使用Lasso Regression模型的均方误差为: 32.9339470534
使用Lasso Regression模型的均方根误差为: 5.7388105957

可以发现对于Lasso或是Ridge都是需要设置 α α (即 λ λ )参数的。我们可以比较一下不同 α α 参数下，模型评分的大小。
此处评分用的是R2score，即决定系数。我们常用决定系数来判断回归模型的拟合程度。

alphas = [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000]
scores1 = []
scores2 = []
for i, alpha in enumerate(alphas):
    model_ridge = linear_model.Ridge(alpha=alpha)
    model_ridge.fit(X_train, y_train)
    scores1.append(model_ridge.score(X_test, y_test))
    model_lasso = linear_model.Lasso(alpha=alpha)
    model_lasso.fit(X_train, y_train)
    scores2.append(model_lasso.score(X_test, y_test))
figure = plt.figure(figsize=(8,6))
ax = figure.add_subplot(1, 1, 1)
ax.plot(alphas, scores1,color='red',lw=1,label='Ridge')
ax.plot(alphas, scores2,lw=1,label='Lasso')
plt.legend(loc='upper right',frameon=False)
ax.set_xlabel(r"$\alpha$")
ax.set_ylabel(r"score")
ax.set_xscale("log")
ax.set_title("Ridge&Lasso")
plt.show()

输出为：

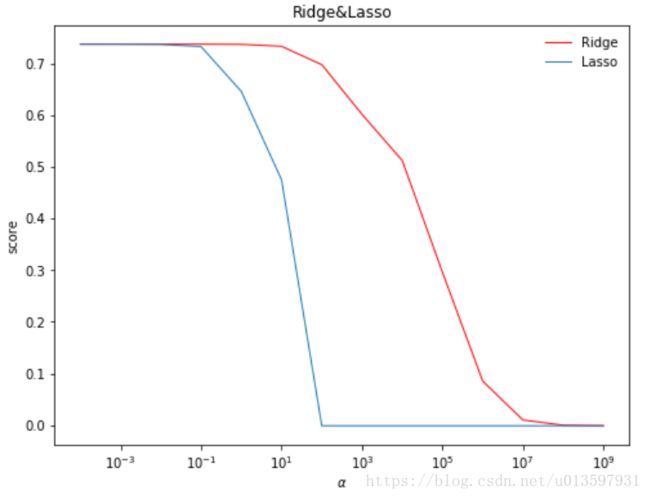
Lasso回归可以使得一些特征的 w w 系数均变成0，增强了模型泛化能力

【Elastic Net】

Elastic Net也是对最小二乘法做了正则化处理，它用一个超参数 ρ ρ 来平衡L1和L2正则化的比重，即 minw||wTx−y||2+λρ||w||+λ(1−ρ)2∑j=1nw2j min w | | w T x − y | | 2 + λ ρ | | w | | + λ ( 1 − ρ ) 2 ∑ j = 1 n w j 2
在Elastic Net中我们需要注意两个超参数，一个是 λ λ (正则化超参数)，一个是 ρ ρ (范数权重超参数)。

【逻辑回归】

这是一个名为回归，实质用于分类问题的线性模型(打入回归队伍的分类间谍2333)
在sklearn中，我们可以使用LogisticRegression这个类来做二分类，也可以用one vs rest的方法做多分类。同时，我们还可以选择L1或者L2正则化来防止过拟合。
对于逻辑回归的实践放在下一篇来写，会参照官方文档来看看这个类中的参数、属性和方法。

官方库中还提供了很多线性模型算法库，就不一一细看了，网上已有总结的博文，大家可以去看。http://www.cnblogs.com/pinard/p/6026343.html

参考：
http://scikit-learn.org/stable/modules/linear_model.html
http://www.cnblogs.com/pinard/p/6026343.html
代码保存于：
https://github.com/htshinichi/ML_practice