序列最小最优化算法(SMO) SVM凸优化求

1998年，由Platt提出的序列最小最优化算法(SMO)可以高效的求解上述SVM问题，它把原始求解N个参数二次规划问题分解成很多个子二次规划问题分别求解，每个子问题只需要求解2个参数，方法类似于坐标上升，节省时间成本和降低了内存需求。每次启发式选择两个变量进行优化，不断循环，直到达到函数最优值。

https://blog.csdn.net/m_buddy/article/details/52496538

1. SMO SVM算法简述
  1.1 概述
SVM（Support Vector Machine，SVM）算法既是支持适量机算法。算法的原始思想很简单，既是找到一个决策面使两类（本文以两类为例进行说明）分开，且这个决策面和两类之间的间隙尽可能的大。这样带来的好处就是泛化错误率低，能够很好地对两类的问题进行分类。
因而，SVM算法的优点就是泛化错误率低，计算的开销不大，结果容易解释。缺点就是算法对参数的选择和核函数的选择敏感，原始的分类器适合二分类。
  1.2 原理
我们定义决策面为：
 

点到面的距离：

在SVM算法中距离决策面近的点的g(x)的值为+1（对应类别X1）或是-1（对应类别X2），因而需要满足的条件为：

公式中的X1和X2对应为两个类别，则公式(3)可以被写为：

由于yi有正负对应上式3，则条件全为大于等于1的

因而对于上述的二次优化问题可以有KKT条件，用拉格朗日方程的形式写出：

 

则将公式(5)中的第一个、第二个式子带入到最后一个式子中，得到：

 

则对(5)最后一个式子最大化，将(6)带入到(5)中的最后一个式子代数运算之后得到的等价的优化为：

 

则通过解上诉的方程组，得到决策面的系数，就可以作为以后的分类使用了。但是上述的方法具有缺陷，它是对应下面分布的情况的，在这样的情况中，能够直接找到一个决策面。但是对于接下来的一种分布情况就不适用了（图片来源于度娘）

 

1.2 情况2

先来看一下这里分析的分类情况（图片来源于网络）：

在这样的分布情况下就出现了3中可能的情况，（1）位于分离段以外并且正确分类的数据；（2）落在分离段内部，但是正确分类了的数据；（3）被错误分类的数据。因而原来的原始约束条件就写为了：

因而，对于情况（1）这里定义的偏移量为0了；情况（2）偏移量就大于0且小于1；情况（3）偏移量大于0。这里引入了偏移量（松弛变量）增加了变量的个数，但是SVM算法的目的是使得分类间隔尽可能大，同时保持偏移量大于0的数据尽可能少。 则原来的最小化函数J就变成了：

 

其中I(x)是0-1的阶跃函数，但是区间为大于等于0。引入了偏移量之后的推导也是跟之前情况的推导是类似的，则最后得到的优化函数为：

2. Platt的SMO算法
  2.1 SMO方法
SMO方法是将原来SVM的二次规划问题转化为固定大小的二次规划子问题。因为SVM算法需要遵循公式(10)中限制条件1，所以SMO方法选择两个λ进行优化。在SMO方法中使用启发式的方法选择两个λ，这样选取会极大加速算法的收敛速度，做过对比证明要比随机的撞天婚方法快很多很多。这是论文中SMO方法更新λ的部分（偷下懒截出来仅供交流），在该论文的2.2节介绍了循环的条件，读者可以下载论文下来进行阅读。 

https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/smo-book.pdf

 

# -*- coding: utf-8 -*-
"""
Created on Sun Jul 22 20:22:19 2018

@author: wzy
"""
import matplotlib.pyplot as plt
import numpy as np
import random

"""
函数说明：读取数据

Parameters:
    fileName - 文件名
    
Returns:
    dataMat - 数据矩阵
    labelMat - 数据标签

Modify:
    2018-07-23
"""
def loadDataSet(fileName):
    # 数据矩阵
    dataMat = []
    # 标签向量
    labelMat = []
    # 打开文件
    fr = open(fileName)
    # 逐行读取
    for line in fr.readlines():
        # 去掉每一行首尾的空白符，例如'\n','\r','\t',' '
        # 将每一行内容根据'\t'符进行切片
        lineArr = line.strip().split('\t')
        # 添加数据(100个元素排成一行)
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        # 添加标签(100个元素排成一行)
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat

"""
函数说明：随机选择alpha_j

Parameters:
    i - alpha
    m - alpha参数个数
    
Returns:
    j - 返回选定的数字

Modify:
    2018-07-23
"""
def selectJrand(i, m):
    j = i
    while(j == i):
        # uniform()方法将随机生成一个实数，它在[x, y)范围内
        j = int(random.uniform(0, m))
    return j

"""
函数说明：修剪alpha

Parameters:
    aj - alpha值
    H - alpha上限
    L - alpha下限
    
Returns:
    aj - alpha值

Modify:
    2018-07-23
"""
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

"""
函数说明：简化版SMO算法

Parameters:
    dataMatIn - 数据矩阵
    classLabels - 数据标签
    C - 松弛变量
    toler - 容错率
    maxIter - 最大迭代次数
    
Returns:
    None

Modify:
    2018-07-23
"""
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    # 转换为numpy的mat矩阵存储(100,2)
    dataMatrix = np.mat(dataMatIn)
    # 转换为numpy的mat矩阵存储并转置(100,1)
    labelMat = np.mat(classLabels).transpose()
    # 初始化b参数，统计dataMatrix的维度,m:行；n:列
    b = 0
    # 统计dataMatrix的维度,m:100行；n:2列
    m, n = np.shape(dataMatrix)
    # 初始化alpha参数，设为0
    alphas = np.mat(np.zeros((m, 1)))
    # 初始化迭代次数
    iter_num = 0
    # 最多迭代maxIter次
    while(iter_num < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            # 步骤1：计算误差Ei
            # multiply(a,b)就是个乘法，如果a,b是两个数组，那么对应元素相乘
            # .T为转置
            fxi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            # 误差项计算公式
            Ei = fxi - float(labelMat[i])
            # 优化alpha，设定一定的容错率
            if((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
                # 随机选择另一个alpha_i成对比优化的alpha_j
                j = selectJrand(i, m)
                # 步骤1，计算误差Ej
                fxj = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
                # 误差项计算公式
                Ej = fxj - float(labelMat[j])
                # 保存更新前的alpha值，使用深拷贝(完全拷贝)A深层拷贝为B，A和B是两个独立的个体
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                # 步骤2：计算上下界H和L
                if(labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j]  -alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if(L == H):
                    print("L == H")
                    continue
                # 步骤3：计算eta
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[j, :] * dataMatrix[j, :].T
                if eta >= 0:
                    print("eta>=0")
                    continue
                # 步骤4：更新alpha_j
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta
                # 步骤5：修剪alpha_j
                alphas[j] = clipAlpha(alphas[j], H, L)
                if(abs(alphas[j] - alphaJold) < 0.00001):
                    print("alpha_j变化太小")
                    continue
                # 步骤6：更新alpha_i
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
                # 步骤7：更新b_1和b_2
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[i, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
                # 步骤8：根据b_1和b_2更新b
                if(0 < alphas[i] < C):
                    b = b1
                elif(0 < alphas[j] < C):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0
                # 统计优化次数
                alphaPairsChanged += 1
                # 打印统计信息
                print("第%d次迭代 样本：%d， alpha优化次数：%d" % (iter_num, i, alphaPairsChanged))
        # 更新迭代次数
        if(alphaPairsChanged == 0):
            iter_num += 1
        else:
            iter_num = 0
        print("迭代次数：%d" % iter_num)
    return b, alphas
                

"""
函数说明：计算w

Returns:
    dataMat - 数据矩阵
    labelMat - 数据标签
    alphas - alphas值
    
Returns:
    w - 直线法向量

Modify:
    2018-07-24
"""
def get_w(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
    # 我们不知道labelMat的shape属性是多少，
    # 但是想让labelMat变成只有一列，行数不知道多少，
    # 通过labelMat.reshape(1, -1)，Numpy自动计算出有100行，
    # 新的数组shape属性为(100, 1)
    # np.tile(labelMat.reshape(1, -1).T, (1, 2))将labelMat扩展为两列(将第1列复制得到第2列)
    # dot()函数是矩阵乘，而*则表示逐个元素相乘
    # w = sum(alpha_i * yi * xi)
    w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
    return w.tolist()

"""
函数说明：分类结果可视化

Returns:
    dataMat - 数据矩阵
    w - 直线法向量
    b - 直线截距
    
Returns:
    None

Modify:
    2018-07-23
"""
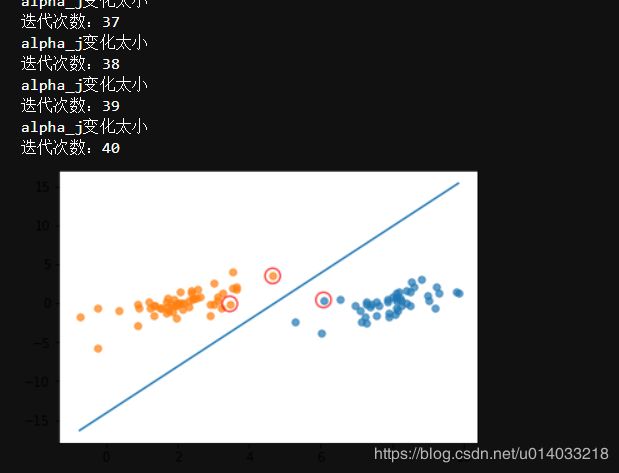
def showClassifer(dataMat, w, b):
    # 正样本
    data_plus = []
    # 负样本
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    # 转换为numpy矩阵
    data_plus_np = np.array(data_plus)
    # 转换为numpy矩阵
    data_minus_np = np.array(data_minus)
    # 正样本散点图（scatter）
    # transpose转置
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)
    # 负样本散点图（scatter）
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7)
    # 绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b - a1 * x1) / a2, (-b - a1 * x2) / a2
    plt.plot([x1, x2], [y1, y2])
    # 找出支持向量点
    # enumerate在字典上是枚举、列举的意思
    for i, alpha in enumerate(alphas):
        # 支持向量机的点
        if(abs(alpha) > 0):
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolors='red')
    plt.show()

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet('testSet.txt')
    b, alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
    w = get_w(dataMat, labelMat, alphas)
    showClassifer(dataMat, w, b)