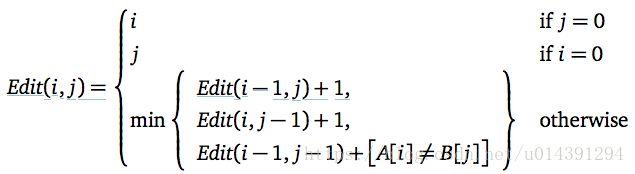动态规划

关于动态规划

动态规划算是面试中最容易考察的一种算法了。它背后的思想很简单，如果我们想要解决一个问题，只要我们能够解决其对应的各个子问题，那么我们就可以根据子问题得到原来问题的解了。

通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

动态规划问题举例

关于动态规划，最简单的一个例子就是Fibonacci序列了。计算Fibonacci序列罪案的算法就是直接按照定义计算，函数递归

function fib（n）
    if n = 0 or n = 1
        return n
    return fib(n − 1) + fib（n − 2）

当 n=5 n = 5 时， fib(5) f i b ( 5 ) 的计算过程如下

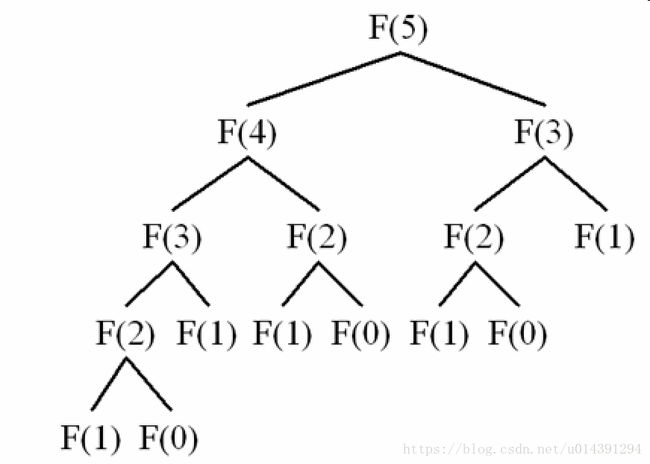
由上面可以看出，这种算法对于相似的子问题进行了重复的计算，因此不是一种高效的算法。实际上，该算法的运算时间是指数级增长的。 改进的方法是，我们可以通过保存已经算出的子问题的解来避免重复计算：

array map [0...n] = { 0 => 0, 1 => 1 }
fib（n）
    if（map m does not contain key n）
        m[n] := fib(n − 1) + fib（n − 2）
    return m[n]

将前 n n 个已经算出的数保存在数组map中，这样在后面的计算中可以直接应用前面的结果，从而避免了重复计算。算法的运算时间变为 O(n) O ( n )

动态规划原理

动态规划的适用于

• 最优子结构性质。
  
  • 如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质
• 无后效性。
  
  • 子问题的解一旦确定，就不再改变，不受在这之后、包含他的更大的问题的求解决策影响
• 子问题重叠性质。
  
  • 在递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正式利用了这种子问题的重叠性质，对每一个子问题只计算义词，然后将其计算结果保存在一个表格中，当再次需要计算已经计算的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

动态规划经典模型

线性模型

区间模型

背包模型

动态规划经典问题

编辑距离(edit distance)

这是一个动态规划问题。我们定义一个二维数组d[i][j]来保存这些编辑最小操作，它表示将串a[0:i-1]转变为b[0:j-1]的最小步骤（a[]和b[]是两个字符数组，从下标0开始初始化）。

然后我们分情况先讨论：

当i = 0时：a串为空，那么转变为b串就是不断添加字符，d[0][j] = j。

当j = 0时：b串为空，那么转变为b串就是不断删除字符，d[i][0] = i。

接下来是一般情况：我们考虑到字符的操作有三种，分别是删除、增加和替换，那么它们的操作就是在前一步的操作下以最少的次数增删改。现在分三种情况：

1）假设把a[1:i] -> b[1:j-1]要x个步骤，那只要在b[j]增加a[i]后面就搞定了，那就需要x+1步操作。

2）假设把a[1:i-1] -> b[1:j]要x个步骤，那么只要在删除a[i]就好了，需要x+1步操作。

3）假设把a[1:i-1] -> b[1:j-1]要x个步骤，那么只需要把a[i]替换为b[j]就ok了，那就需要x+1步操作。如果a[i] == b[j]，只需要x步。

所以填表法的思想来讲，就是从上面三种情况中选最小的，填入表格中。

最长公共子序列(Longest Common Subsequence, LCS)

对于序列 X[1..m] X [ 1.. m ] 和 Y[1..n] Y [ 1.. n ]

Computing the length of the LCS

function LCSLength(X[1..m], Y[1..n])
    C = array(0..m, 0..n)
    for i := 0..m
       C[i,0] = 0
    for j := 0..n
       C[0,j] = 0
    for i := 1..m
        for j := 1..n
            if X[i] = Y[j]
                C[i,j] := C[i-1,j-1] + 1
            else
                C[i,j] := max(C[i,j-1], C[i-1,j])
    return C[m,n]

Reading out a LCS

function backtrack(C[0..m,0..n], X[1..m], Y[1..n], i, j)
    if i = 0 or j = 0
        return ""
    if  X[i] = Y[j]
        return backtrack(C, X, Y, i-1, j-1) + X[i]
    if C[i,j-1] > C[i-1,j]
        return backtrack(C, X, Y, i, j-1)
    return backtrack(C, X, Y, i-1, j)

Reading out all LCSs

function backtrackAll(C[0..m,0..n], X[1..m], Y[1..n], i, j)
    if i = 0 or j = 0
        return {""}
    if X[i] = Y[j]
        return {Z + X[i] for all Z in backtrackAll(C, X, Y, i-1, j-1)}
    R := {}
    if C[i,j-1] ≥ C[i-1,j]
        R := R ∪ backtrackAll(C, X, Y, i, j-1)
    if C[i-1,j] ≥ C[i,j-1]
        R := R ∪ backtrackAll(C, X, Y, i-1, j)
    return R

最长递增子序列(Longest Increasing Subsequence,lis)

问题：
对于一个序列如1，-1，2，-3，4，-5，6，-7，其最长第增子序列为1,2,4,6。

背包问题

Vieterbi算法