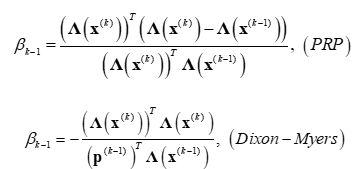多维无约束优化算法

在没有任何限制条件下寻求目标函数的极小点：
$$\underset{x\in R^n}{\min }f(x)$$
求解方法有多种，主要不同点在于如何构造搜索方向

最速下降法

基本思想

在每次迭代中，沿最速下降方向（负梯度方向）进行搜索，每一步沿负梯度方向取最优步长。

• 只以一阶梯度的信息确定下一步的方向，收敛速度慢；越接近极值点，收敛越慢
• 一般用于最优化开始的几步搜索

分析

由泰勒公式：
$$\mathbf{f}(\mathbf{x}+\lambda \mathbf{p})=\mathbf{f}(\mathbf{x})+\lambda {\mathbf{\Lambda }}^{\mathbf{T}}(\mathbf{x})\mathbf{p}+\mathbf{o}(\lambda ||\mathbf{p}||)(\lambda >0)$$
由于${\mathbf{\Lambda }}^{\mathbf{T}}(\mathbf{x})\mathbf{p}=-||{\mathbf{\Lambda }}^{\mathbf{T}}(\mathbf{x})||||\mathbf{p}||\mathbf{c}\mathbf{o}\mathbf{s}\theta$，$\theta$为$\mathbf{p}$与$-\mathbf{\Lambda }(\mathbf{x})$的夹角，当$\lambda$和$||p||$固定时，取$cos\theta =1$可使${\Lambda }^T(x)p$取最小值，$f(x)$下降最多。即当$\theta =0$时，$f(x)$下降最快，此时有$\mathbf{p}=-\nabla \mathbf{f}(\mathbf{x})$。

从而算法的搜索方向$p^{(k)}$为负梯度方向$-\nabla f(x)$。故算法的迭代式为;
$$x^{(k+1)}=x^{(k)}-{\lambda }_k\nabla f(x^{(k)})$$

算法步骤

(1) 选取初始点估计值$x^{(0)}$，确定允许误差$\epsilon$，令$k=0$

(2) 计算目标函数在$x^{(k)}$处的负梯度$ - \nabla (x^{(k)})$

(3) 检查收敛性，若$||\nabla (x^{(k)})||\le \epsilon$，则$x^{\ast }=x^{(k)}$,计算终止，否则继续

(4) 确定搜索方向

​ 负梯度方向的单位向量：$p^{(k)}=\frac{-\nabla (x^{(k)})}{||\nabla (x^{(k)})||}$

(5) 一维搜索

​ 以$x^{(k)}$为起点，沿负梯度方向$p^{(k)}$进行一维搜索，求得最优步长${\lambda }_k$。使得：
$$f(x^{(k)}+{\lambda }_k{p}^{(k)})=\underset{\lambda >0}{\min }f(x^{(k)}+\lambda p^{(k)})$$
下一个迭代点为:
$$x^{(k+1)}=x^{(k)}-{\lambda }_k{p}^{(k)}$$
(6) $k=k+1$，转(2)。

特点

• 有很好的全局收敛性，任意初始点开始迭代，所产生的点列均收敛。
• 收敛速度比较慢。所谓“最速方向”，仅仅反映函数$f(x)$在点$x^{(k)}$的局部性质，对整体来说，不一定就是下降最快的方向
• 由最优步长${\lambda }_k$的意义知：$(p^{(k)}{)}^T\nabla f(x^{(k+1)})=0$，所以在相邻两次迭代中，搜索方向是相互正交的。

牛顿法

基本思想

每次迭代时，用适当的二次函数近似目标函数，并用迭代点指向近似二次函数极小点的方向来构造搜索方向。

分析

$f$有二阶连续偏导数，$x^{(k)}$是$f$的极小点的第$k$次近似，$f$在近似点$x^{(k)}$处泰勒展开，二阶近似:
$$f(x)\approx \phi (x)=f(x^{(k)})+\nabla (x^{(k)}{)}^T(x-x^{(k)})+\frac{1}{2}(x-x^{(k)}{)}^{T}H(x^{(k)})(x-x^{(k)})$$
易见 $\phi (x)$是二次函数，求它的极小值：令
$$\nabla \phi (x)=\nabla (x^{(k)})+H(x^{(k)})(x-x^{(k)})=0$$
若Hessian矩阵$H(x^{(k)})$正定，则$\phi (x)$的驻点就是$\phi (x)$的极小点。以它作为$f$的极小点的第$k+1$次近似，记为$x^{(k+1)}$，即:
$$x^{(k+1)}=x^{(k)}+H^{-1}(x^{(k)})\nabla (x^{(k)})$$
此式即为牛顿法迭代公式。

算法步骤

(1) 选取初始点估计值$x^{(0)}$，确定允许误差$\epsilon$，令$k=0$

(2) 计算目标函数在$x^{(k)}$处的梯度$\nabla (x^{(k)})$

(3) 检查收敛性，若$||\nabla (x^{(k)})||\le \epsilon$，则$x^{\ast }=x^{(k)}$,计算终止，否则继续

(4) 构造牛顿方向：$p^{(k)}=H^{-1}(x^{(k)})\nabla (x^{(k)})$

(5) 更新点列：$x^{(k+1)}=x^{(k)}+p^{(k)}$

(6) $k=k+1$，转(2)。

特点

• 要求$f(x)$是二阶可微函数，有时计算hessian矩阵的逆矩阵十分困难
• 初始点与极小点的距离不宜太短，较远的话hessian矩阵奇异，此时牛顿方向可能不存在，迭代可能不收敛，甚至下降性也不能保证。

拟牛顿法

就是用梯度差分或者一个近似矩阵$H_k$去代替$H^{-1}(x^{(k)})$，以克服牛顿法中需要计算$H^{-1}(x^{(k)})$的缺点。

不同构造$H_k$的方法，产生不同的拟牛顿法。

特点

• 仅需要一阶导数
• 保持正定，使方法具有下降性质
• 每次迭代需要$o(n^2)$次乘法运算，牛顿法需要$o(n^4)$
• 搜索方向相互共轭，具有二次终止性

阻尼牛顿法

基本思想

选择较优目标值的初始点是困难的，需要对牛顿法进行修正。

牛顿法中，假设${\lambda }_k=1$，但在阻尼牛顿法中，每一次的迭代需要计算搜索因子${\lambda }_k$,进行一次一维搜索，以保证算法的收敛或者加快收敛速度。

分析

首先确定搜索方向：
$$p^{(k)}=-{\nabla }^{2}f(x^{(k)}{)}^{-1}\nabla (f(x^{(k)}))$$
然后求解一元函数寻优问题：
$$f(x^{(k)}+{\lambda }_k{p}^{(k)})=\underset{\lambda >0}{\min }f(x^{(k)}+\lambda p^{(k)})$$
得到阻尼牛顿法新的迭代点公式：
$$x^{(k+1)}=x^{(k)}+{\lambda }_k{p}^{(k)}$$

算法步骤

(1) 选取初始点估计值$x^{(0)}$，确定允许误差$\epsilon$，令$k=0$

(2) 计算目标函数在$x^{(k)}$处的梯度$\nabla (x^{(k)})$

(3) 检查收敛性，若$||\nabla (x^{(k)})||\le \epsilon$，则$x^{\ast }=x^{(k)}$,计算终止，否则继续

(4) 构造牛顿方向：$p^{(k)}=H^{-1}(x^{(k)})\nabla (x^{(k)})$

沿着$p^{(k)}$进行一维搜索求得最优搜索因子${\lambda }_k$：
$$f(x^{(k)}+{\lambda }_k{p}^{(k)})=\underset{\lambda >0}{\min }f(x^{(k)}+\lambda p^{(k)})$$
(5) 更新点列：$x^{(k+1)}=x^{(k)}+{\lambda }_k{p}^{(k)}$

(6) $k=k+1$，转(2)。

特点

• 保持了牛顿法收敛速度快的特点，降低了对初始点的选择要求

• 由此得到的点列$\{x^{(k)}\}$有如下性质;

  ​ (1) $\{f(x^{(k)})\}$为严格单调下降数列

  ​ (2) $\{x^{(k)}\}$的任一极限点$\hat{x}$必为$f(x)$的极小点

共轭方向法

基本思想

牛顿法收敛速度快，但是计算困难，梯度法计算简便，但是收敛速度较慢。

结合优点，就有了共轭方向法。

原理就是利用矩阵A的共轭向量组作为搜索方向。

分析

背景知识;

$p_i$是A-共轭向量系是指：

对于对称矩阵A，$p_i(i=1,2,...,m;m<n)$为m维列向量组，满足$(p_i,p_j{)}_A=p_i^{T}A{p}_j=0(i\ne j)$。

n阶正定阵A，$p_i\ne 0,(i=0,1,...,n-1)$为A的共轭向量系，对于$\forall v\in R^n$，有$v={\sum }_{i=0}^{n-1}\frac{p_i^{T}Av}{p_i^{T}A{p}_i}{p}_i$。

n阶正定阵A，$p_i\ne 0,(i=0,1,...,n-1)$为A的共轭向量系，且二次函数式从n维欧式空间的任何初始点$x^{(0)}$开始，顺次沿着$p_i$方向作m次搜索得到$x^{(m)}$，则;

1. $p_i^T\nabla (x^{(m)})=0,(i=0,1,...,m-1)$
2. 若$m=n$，则$x^{(n)}$就是$f(x)$的极小值点

对任意选取的初始值$x^{(0)}$，至多迭代n步就可以收敛到$f(x)$的全局极小点$x^{\ast }$。

对于任何一组线性无关的向量$v_i(i=0,1,...,n-1)$，求取矩阵A的一组共轭向量的算法为：
$$p_0=v_0,p_i=v_i-\sum _{j=0}^{i-1}\frac{p_j^{T}A{v}_i}{p_{j}A{p}_j}{p}_j(j=1,2,...,n-1)$$
算法执行过程中，为简便计算，可取$v_i$ 为单位阵中的列向量。

得到共轭向量组$p_i(i=0,1,...,n-1)$，然后令下降方向为：$p^{(k)}=p_k(k=0,1,...,n-1)$，并且${\lambda }_k$由一维搜索确定。

note: 算法中函数$f(x)$是用二阶泰勒展开式近似的，所以得到的最优解可能还不是极小点，因此可将该最优解作为初始值在进行一轮迭代，一般要重复多次，逐步达到极小点。

算法步骤

(1) 选取初始点估计值$x^{(0)}$，确定允许误差$\epsilon$，令$k=0$

(2) 令$p^{(0)}=p_0=v_0$，计算$\nabla (x^{(0)})$

(3) 沿着$p^{(k)}$进行一维搜索求得最优搜索因子${\lambda }_k$：
$$f(x^{(k)}+{\lambda }_k{p}^{(k)})=\underset{\lambda >0}{\min }f(x^{(k)}+\lambda p^{(k)})$$
计算得到下一个迭代点：

$x^{(k+1)}=x^{(k)}+{\lambda }_k{p}^{(k)}$

(4) $k=k+1$，计算$\nabla (x^{(k)})$

(5) 检查收敛性，若$||\nabla (x^{(k)})||\le \epsilon$，则$x^{\ast }=x^{(k)}$,计算终止，否则继续

(6) 循环变量检查：若$k=n$，则转(8)，否则继续

(7) 计算$$p^{(k)}=p_k=v_k-\sum _{j=0}^{k-1}\frac{p_j^{T}A{v}_k}{p_{j}A{p}_j}{p}_j$$，转（3）

(8) 开始下一轮迭代：令$x^{(0)}=x^{(n)},p^{(0)}=p_0=v_0,\nabla (x^{(0)})=\nabla (x^{(n)})$，转（3）

共轭梯度法

基本思想

在共轭方向法中，选取不同的初始线性无关向量组$v_i$ ，可以得到不同的A-共轭向量组。

共轭梯度法，试讲目标函数在各点的负梯度$-\nabla (x(i)),(i=0,1,....,n-1)$作为共轭方法中的线性无关向量组$v_i(i=0,1,....,n-1)$，从而构成A的共轭向量组$p_i(i=0,1,....,n-1)$。

算法步骤

(1) 选取初始点估计值$x^{(0)}$，确定允许误差$\epsilon$，令$k=0$

(2) 计算$\nabla (x^{(0)})$，令$p^{(0)}=-\nabla (x^{(0)})$

(3) 一维搜索求得最优搜索因子${\lambda }_k$：
$$f(x^{(k)}+{\lambda }_k{p}^{(k)})=\underset{\lambda >0}{\min }f(x^{(k)}+\lambda p^{(k)})$$
计算得到下一个迭代点：

$x^{(k+1)}=x^{(k)}+{\lambda }_k{p}^{(k)}$

(4) $k=k+1$，计算$\nabla (x^{(k)})$

(5) 检查收敛性，若$||\nabla (x^{(k)})||\le \epsilon$，则$x^{\ast }=x^{(k)}$,计算终止，否则继续

(6) 循环变量检查：若$k=n$，则转(8)，否则继续

(7) 计算$p^{(k)}=-\nabla (x^{(k)})+\frac{(\nabla (x^{(k)}){)}^{T}A{p}^{(k-1)}}{(p^{(k-1)}{)}^{T}A{p}^{(k-1)}}{p}^{(k-1)}$

转(3)

(8) 开始下一轮迭代：令$x^{(0)}=x^{(n)},p^{(0)}=-\nabla (x^{(0)})$，转（3）

note

(7)中使用矩阵A，对于二次型函数，A已经存在，非二次型函数，可以用$H(x^{(k)})$代替矩阵A，这样一来计算量很大。

用FR公式避免Hessian矩阵的计算，(7)中公式改写为：$p^{(k)}=-\nabla (x^{(k)})+{\beta }_{k-1}{p}^{(k-1)}$.

经过推导，得到FR公式为：
$${\beta }_{k-1}=\frac{(\nabla (x^{(k)}){)}^T\nabla (x^{(k)})}{(\nabla (x^{(k-1)}){)}^T\nabla (x^{(k-1)})}=\frac{||\nabla (x^{(k)})|{|}^2}{||\nabla (x^{(k-1)})|{|}^2}$$
步骤(7) 改写为：

计算${\beta }_{k-1},p^{(k)}=-\nabla (x^{(k)})+{\beta }_{k-1}{p}^{(k-1)}$,转（3）

此外还有PRF与DM公式。

变尺度法（DFP）

拟牛顿法的一种，变尺度法是求解无约束极值问题的一种有效方法。为克服梯度法收敛慢和Newton法计算工作量大的缺点而提出来的一种算法

基本思想

梯度法中，沿最速下降方向搜索，有局部特征，产生拉锯现象，收敛较慢，沿牛顿方向收敛快，但是计算Hessian矩阵困难。

因此，构造矩阵$H_k$按照：
$$p^{(k)}=-H_k\nabla (x^{(k)})$$
选择搜索方向。

为保证下降方向且计算简便，要求$H_k$;

• 正定
• 递推关系$H_{k+1}=H_k+\Delta H_k$

DFP算法

$$\Delta H_k=\frac{\Delta x^{(k)}(\Delta x^{(k)}{)}^T}{(\Delta x^{(k)}{)}^T{q}_k}-\frac{H_k{q}_k{q}_k^T{H}_k}{q_k^T{H}_k{q}_k}$$

BFGS 算法

$$\begin{gathered} \Delta H_k=\frac{q_k^T{H}_k{q}_k\Delta x^{(k)}(\Delta x^{(k)}{)}^T}{((\Delta x^{(k)}{)}^T{q}_k{)}^2}-\frac{\Delta x^{(k)}{q}_k^T{H}_k}{(\Delta x^{(k)}{)}^T{q}_k}-\frac{H_k{q}_k(\Delta x^{(k)}{)}^T}{(\Delta x^{(k)}{)}^T{q}_k}+\frac{\Delta x^{(k)}(\Delta x^{(k)}{)}^T}{(\Delta x^{(k)}{)}^T{q}_k} \\ =(I-\frac{\Delta x^{(k)}{q}_k^T}{(\Delta x^{(k)}{)}^T{q}_k})H_k(I-\frac{\Delta x^{(k)}{q}_k^T}{(\Delta x^{(k)}{)}^T{q}_k})+\frac{\Delta x^{(k)}(\Delta x^{(k)}{)}^T}{(\Delta x^{(k)}{)}^T{q}_k} \end{gathered}$$

$q_k=\nabla (x^{(k+1)})-\nabla (x^{(k)})$

算法流程

(1) 选取初始点估计值$x^{(0)}$，确定允许误差$\epsilon$，选取初始矩阵$H_0=I$

(2) 计算$f_0=f(x^{(0)}),{\nabla }_0=\nabla (x^{(0)})$，令$p^{(0)}=-{\nabla }_0,k=0$

(3) 检查收敛性，若$||{\nabla }_0||\le \epsilon$，则$x^{\ast }=x^{(0)}$,计算终止，否则继续

(4) 一维搜索求得最优步长${\lambda }_k$：
$$f(x^{(k)}+{\lambda }_k{p}^{(k)})=\underset{\lambda >0}{\min }f(x^{(k)}+\lambda p^{(k)})$$
计算得到下一个迭代点：

$x^{(k+1)}=x^{(k)}+{\lambda }_k{p}^{(k)}$

之后计算$f_{k+1}=f(x^{(k+1)}),{\nabla }_{k+1}=\nabla (x^{(k+1)})$

(5) 检查收敛性，若$||{\nabla }_{k+1}||\le \epsilon$，则$x^{\ast }=x^{(k+1)}$,计算终止，否则继续

(6) 正定检查，即检查函数值是否下降，若$f_{k+1}\ge f_k$，则令$x^{(0)}=x^{(}k),f_0=f_k,{\nabla }_0={\nabla }_k,H_0=I,k=0$，转（4），否则继续

(7) 检查迭代次数：

若$k=n-1$，则转(9)，否则继续

(8) 计算$q_k=\nabla (x^{(k+1)})-\nabla (x^{(k)})$,使用DFP算法或者BFGS算法计算$H_{k+1}$，确定搜索方向$p^{(k+1)}=-H_{k+1}\nabla (x^{(k+1)})$，令$k=k+1$,转（3）

(9) 令$x^{(0)}=x^{(}n),f_0=f_n,{\nabla }_0={\nabla }_n,H_0=I,k=0$，转（4）

特点

• 避免二阶导数矩阵及其求逆计算
• 比梯度法收敛速度快

编程数值计算多元函数的梯度和海因矩阵。

小结

多维无约束优化算法，其中变尺度法迭代中选取的搜索方向是共轭的，故将变尺度法和共轭梯度法归结为一类算法。