带权图的最小生成树 及其java实现
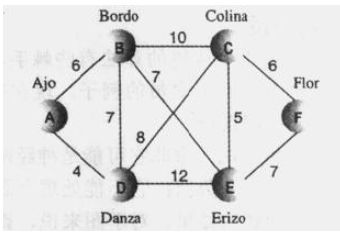
如图所示:选择哪些边架设电缆,能使得安装有线电视系统的造价最低呢?
方法是利用最小生成树,它将有5条边(比城市数量少1),连接6个城市,并具有建立连接所需的最小代价。
设计算法:
算法要点:下面是用图的术语重申一下算法。
从一个顶点开始,把它放入树的集合。然后重复做下面的事情:
1.找到从最新的顶点到其他顶点的所有边,这些顶点不能在树的集合中。把这些边放入优先级队列。
2.找出权值最小的边,把它和它所达到的顶点放入树的集合中。
重复这些步骤,直到所有顶点都在树的集合中,这时,工作完成。
java代码:根据前面的算法要点,
编制有向图最小生成树的方法mstw() .正如其他图的程序一样,假设在vertexList[] 数组中有一个顶点列表,并且从下标为0的顶点开始。currentVert代表最近加到树中的顶点。下面是mstw()方法的代码:
/*
* 算法在while中执行,循环结束条件是所有的顶点都已经在树中。循环完成类下面的操作
* 1.当前顶点放在树中
* 2.连接这个顶点的边放在优先级队列中
* 3.从优先级队列中删除权值最小的边。这条边的目的顶点变成当前顶点
*/
public void mstw()
{
currentVert = 0;
while(nTree < nVerts -1 )// while not all verts in tree
{
//put currentVert in tree
vertexList[currentVert].isInTree = true;
nTree ++;
for(int j=0;j//原点和终点相同,不能放入优先级队列
if(j == currentVert)
continue;
//终点在树中,不能放入优先级队列
if(vertexList[j].isInTree)
continue;
int distance = adjMat[currentVert][j];
//原点和终点之间没有边,不能放入优先级队列
if(distance == INFINITY)
continue;
putInPQ(j,distance);
}
if(thePQ.size() == 0)
{
System.out.println("GRAPH NOT CONNECTED");
return;
}
//将最小权值的边从优先级队列中删除,把这条边和这条边的终点加入树,并显示原点和终点
//remove edge with minimum distance, from PQ
Edge theEdge = thePQ.removeMin();
int sourceVert = theEdge.srcVert;
currentVert = theEdge.destVert;
//dispaly edge from source to current
System.out.print(vertexList[sourceVert].label);
System.out.print(vertexList[currentVert].label);
System.out.print(" ");
}
/*
* 所有顶点的isInTree遍历被重置,即从树中删除。
* 因为根据这些数据只能创建一棵树。然而,在完成一项工作后,最好把数据恢复到原来的状态
*/
for(int j = 0;jfalse;
}
————————————————————————-
带权图的最小生成树完整代码:
class Edge
{
public int srcVert ; //index of a vertex starting edge 起点
public int destVert;//index of vertex ending edge 终点
public int distance; // distance from src to dest 之间的距离
//.............................
public Edge(int sv,int dv,int d) //构造方法
{
srcVert = sv;
destVert = dv;
distance =d;
}
}
//////////////////////////////////////////////
//优先级队列 用数组实现。 把相连边都放在优先级队列中
class PriorityQ
{
//array in sorted order,from max at 0 to min at size-1
private final int SIZE = 20;
private Edge[] queArray;
private int size;
//............................
public PriorityQ()
{
queArray = new Edge[SIZE];
size = 0;
}
//....................
//insert item in storted oeder 在优先级队列在插入边
public void insert(Edge item)
{
int j;
for(j = 0;jif(item.distance >= queArray[j].distance)
break;
for(int k=size-1;k>= j;k--)
queArray[k+1] = queArray[k];
queArray[j] = item;
size++;
}
//............................
// 从优先级队列中移除最短边的方法
public Edge removeMin()
{
return queArray[--size];
}
//......................
//删除任意一个数据项的方法
public void removeN(int n)
{
for(int j=n;j1;j++)
queArray[j] = queArray[j+1];
size -- ;
}
//.........................
//得到最小数据项的方法
public Edge peekMin()
{
return queArray[size-1];
}
//.............................
public int size()
{
return size;
}
//...............
public boolean isEmpty()
{
return (size == 0);
}
//......................
// 得到任意一个数据项的方法
public Edge peekN(int n)
{
return queArray[n];
}
//.......................
public int find(int findDex) //find item with specified
{
for (int i = 0; i < size; i++)
if(queArray[i].destVert == findDex)
return i;
return -1;
}
}
/////////////////////////////////////
class Vertex
{
public char label;
public boolean isInTree;
//...................
public Vertex(char lab)
{
label = lab;
isInTree = false;
}
}
//////////////////////////////////
class Graph
{
private final int MAX_VERTS = 20;
private final int INFINITY = 1000000;
private Vertex vertexList[];
private int adjMat[][];
private int nVerts;
private int currentVert;
private PriorityQ thePQ;
private int nTree;
//.........................
public Graph()
{
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int i = 0; i >MAX_VERTS; i++)
for (int j = 0; j new PriorityQ();
}
//.........................
public void addVertex(char lab)
{
vertexList[nVerts ++] = new Vertex(lab);
}
//.......................
public void addEdge(int start,int end,int weight)
{
adjMat[start][end] = weight;
adjMat[end][start] = weight;
}
//......................
public void displayVertex(int v)
{
System.out.print(vertexList[v].label);
}
//..............................
/*
* 算法在while中执行,循环结束条件是所有的顶点都已经在树中。循环完成类下面的操作
* 1.当前顶点放在树中
* 2.连接这个顶点的边放在优先级队列中
* 3.从优先级队列中删除权值最小的边。这条边的目的顶点变成当前顶点
*/
public void mstw()
{
currentVert = 0;
while(nTree < nVerts -1 )// while not all verts in tree
{
//put currentVert in tree
vertexList[currentVert].isInTree = true;
nTree ++;
for(int j=0;j//原点和终点相同,不能放入优先级队列
if(j == currentVert)
continue;
//终点在树中,不能放入优先级队列
if(vertexList[j].isInTree)
continue;
int distance = adjMat[currentVert][j];
//原点和终点之间没有边,不能放入优先级队列
if(distance == INFINITY)
continue;
putInPQ(j,distance);
}
if(thePQ.size() == 0)
{
System.out.println("GRAPH NOT CONNECTED");
return;
}
//将最小权值的边从优先级队列中删除,把这条边和这条边的终点加入树,并显示原点和终点
//remove edge with minimum distance, from PQ
Edge theEdge = thePQ.removeMin();
int sourceVert = theEdge.srcVert;
currentVert = theEdge.destVert;
//dispaly edge from source to current
System.out.print(vertexList[sourceVert].label);
System.out.print(vertexList[currentVert].label);
System.out.print(" ");
}
/*
* 所有顶点的isInTree遍历被重置,即从树中删除。
* 因为根据这些数据只能创建一棵树。然而,在完成一项工作后,最好把数据恢复到原来的状态
*/
for(int j = 0;jfalse;
}
/*
* 在优先级队列中应该只有一条到达某个特定目标顶点的边。putInPQ()方法保证类这一点
* 它调用PriorityQ类的find()方法,这个方法经过修正,可以寻找到到达指定点的边
*/
public void putInPQ(int newVert,int newDist)
{
//is there annther edge with the same destination vertex?
int queueIndex = thePQ.find(newDist); // got edge's index
if(queueIndex != -1) // if there one
{ // get edge
Edge tempEdge = thePQ.peekN(queueIndex);
int oldDist = tempEdge.distance;
if(oldDist > newDist) //if new edge shorter
{
thePQ.removeN(queueIndex); //remove old edge
Edge theEdge = new Edge(currentVert,newVert,oldDist);
thePQ.insert(tempEdge); // insert new edge
}
}
else
{
Edge theEdge = new Edge(currentVert, newVert, newDist);
thePQ.insert(theEdge);
}
}
}
//.............................
class MSTWApp
{
public static void main(String[] args)
{
Graph theGraph = new Graph();
theGraph.addVertex('A');
theGraph.addVertex('B');
theGraph.addVertex('C');
theGraph.addVertex('D');
theGraph.addVertex('E');
theGraph.addVertex('F');
theGraph.addEdge(0, 1, 6);
theGraph.addEdge(0, 3,4);
theGraph.addEdge(1, 2, 10);
theGraph.addEdge(1, 3, 7);
theGraph.addEdge(1, 4, 7);
theGraph.addEdge(2, 3, 8);
theGraph.addEdge(2, 4, 5);
theGraph.addEdge(2, 5, 6);
theGraph.addEdge(3, 4, 12);
theGraph.addEdge(4, 5, 7);
System.out.print("Minium sapnning tree:");
theGraph.mstw();
System.out.println();
}
}