如何写一颗二叉树(递归)【菜鸟学习日记】
老规矩,开篇点题,今天写了二叉树,整理总结一下
二叉树我是用链表来实现的
1、每一个节点包含数据,左指针和右指针,分别指向左孩子和右孩子
//创建节点类型
//节点中有数据,有指针
template<class T>
struct BinaryTreeNode
{
T _data;//数据
BinaryTreeNode *_left;//左孩子
BinaryTreeNode *_right;//右孩子
//初始化
BinaryTreeNode(const T&x)
:_data(x)
, _left(NULL)
, _right(NULL)
{}
}; 2、然后开始创建一个二叉树类
并创建树的各个节点
思路:

‘#’是我们这里用到的标识符(invalid),用来标记的,当然也可以用其它的,当遇到#就代表为空,没有节点了
从根节点开始按前序的顺序遍历创建(这里的遍历用了递归的方法)
class BinaryTree
{
typedef BinaryTreeNode Node;
public:
BinaryTree(T* a,size_t n,const T&invalid)
{
size_t index = 0;
_root = GreateTree(a, n, invalid, index);
}
Node* GreateTree(T* a, size_t n, const T&invalid,size_t &index)
{
//根->左子树->右字树
Node* root = NULL;
if (a[index] != invalid)
{
root = new Node(a[index]);//创建根节点
root->_left = GreateTree(a, n, invalid, ++index);//左树
root->_right = GreateTree(a, n, invalid, ++index);//右树
}
return root;
}
protected:
Node* _root;//根节点
}; 3、创建好一棵树,就可以实现它的其它接口了
前序、种序、后续遍历,遍历其实就是
打印的顺序不同
有一点要注意的是,因为我们遍历时要有根节点参数,但类外拿不到树的根节点,所以再写一些要用根节点的接口时,要有一个无参类型的函数,在类的内部再将根节点传参访问
//前序遍历
void PrevOrder()
{
PrevOrder(_root);
}
//根->左->右
void PrevOrder(Node* root)
{
//为空树,返回
if (root == NULL)
{
return;
}
//不为空树
cout << root->_data <<" ";
PrevOrder(root->_left);
PrevOrder(root->_right);
}
//中序
void MidOrder()
{
MidOrder(_root);
}
//左->根->右
void MidOrder(Node* root)
{
if (root == NULL)
{
return;
}
MidOrder(root->_left);
cout << root->_data <<" ";
MidOrder(root->_right);
}
//后序
void PostOrder()
{
PostOrder(_root);
}
//左->右->根
void PostOrder(Node* root)
{
if (root == NULL)
{
return;
}
PostOrder(root->_left);
PostOrder(root->_right);
cout << root->_data <<" ";
}//测试一下
void TestBinaryTree()
{
int arr[] = { 1, 2, 3, '#', '#', 4, '#', '#', 5, '#', '#'};
BinaryTree<int> t(arr, sizeof(arr) / sizeof(int), '#');
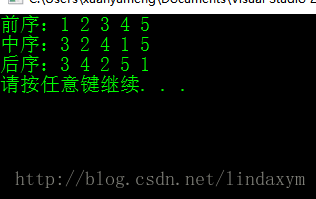
cout << "前序:";
t.PrevOrder();
cout << endl;
cout << "中序:";
t.MidOrder();
cout << endl;
cout << "后序:";
t.PostOrder();
cout << endl;
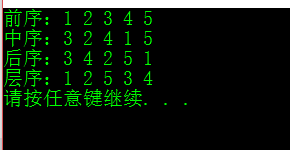
}还有一种层序遍历
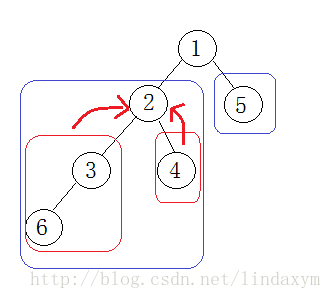
层序遍历与前面三种实现的方法不太一样,层序的遍历要借助一个队列来实现
先将根节点入队列,然后将其左右孩子入队列,将队头Pop;
每次将队头的左右孩子入队,Pop队头,就可以实现层序遍历了
//层序
void LevelOrder()
{
LevelOrder(_root);
}
void LevelOrder(Node* root)
{
if (root == NULL)
{
return;
}
//借助栈来实现
//栈里放指向节点的指针
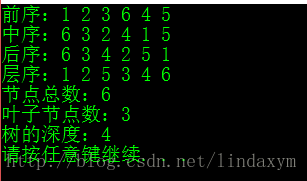
queue实现了四种遍历的接口,接下来该实现计算节点的几种接口了,还有计算深度的接口
- 计算节点总数
- 计算叶子节点数
- 计算第K层的节点数
- 树的深度
计算节点的总数
可以有两种思路
- 遍历,计数
- 将其转化为子问题,节点总数=左子树+右子树+根
实现一下:
//节点总数
//方法一:遍历
//size_t Size()
//{
// size_t size = 0;//计数
// Size(_root,size);
// return size;
//}
//size_t Size(Node* root,size_t &size)
//{
// if (root == NULL)
// {
// return 0;
// }
//遍历计数
// size++;
// Size(root->_left, size);
// Size(root->_right, size);
// return size;
//}
//方法二:转化为子问题
size_t Size()
{
return Size(_root);
}
size_t Size(Node* root)
{
if (root == NULL)
{
return 0;
}
//左子树+右子树+根
return Size(root->_left) + Size(root->_right)+1;
}计算叶子节点数
这个问题也是跟上一个问题一样两种思路,遍历或者转化为子问题
//方法一:遍历
//size_t LeafSize()//叶子节点数
//{
// size_t size = 0;
// LeafSize(_root,size);
// return size;
//}
//size_t LeafSize(Node* root,size_t &size)
//{
// if (root == NULL)
// {
// return 0;
// }
// if (root->_left == NULL&&root->_right == NULL)
// {
// size++;
// }
// LeafSize(root->_left,size);
// LeafSize(root->_right,size);
// return size;
//}
//方法二:子问题
size_t LeafSize()//叶子节点数
{
return LeafSize(_root);
}
size_t LeafSize(Node* root)
{
if (root == NULL)
{
return 0;
}
//是叶子节点,返回1
if (root->_left == NULL&&root->_right == NULL)
{
return 1;
}
//不是叶子节点,再向下递归
return LeafSize(root->_left)+LeafSize(root->_right);
}计算第K层的节点数

这里我们虽然要求的是第k层的节点数,但是我们无法直接到达第k层,我们依然要从根节点开始逐层进入,直到k==1,我们就到达了我们要求的那层了,也就是我们递归结束的标志
然后,再来将问题转化为子问题,第k层的节点数=第k-1层的左子树+右子树节点
这里要注意的是,参数不能用k的引用,因为如果用了引用,当
我们访问完左子树时,k已经被修改,再访问右子树时,会出错
size_t GetKLevel(size_t k)//第k层节点数
{
return _GetKLevel(_root,k);
}
size_t _GetKLevel(Node* root,size_t k)//这里注意不能用k的引用
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
//k==1
if (k == 1)
{
return 1;
}
//k>1,第k层的节点数=第k-1层的左子树+右子树节点
if (k > 1)
{
return _GetKLevel(root->_left, k - 1) + _GetKLevel(root->_right, k - 1);
}
}树的深度
这个问题也同样转化为子问题解决
思路:树的深度=左右子树深度大的+1,每一个子树都是如此,递归就行了
//深度
size_t Depth()
{
return Depth(_root);
}
size_t Depth(Node* root)
{
if (root == NULL)
{
return 0;
}
//为最底层叶子时,返回1
if (root->_left == NULL&&root->_right == NULL)
{
return 1;
}
//否则,返回左右子树大的+1
return Depth(root->_left) > Depth(root->_right) ?
Depth(root->_left) + 1 : Depth(root->_right) + 1;
}