用python自己搭建网络实现mnist手写体识别

纯python实现mnist手写体数字识别

前言

  最近两天开始写自己学习深度学习以来第一个完全从底层不依赖其他深度学习工具的神经网络，实现mnist手写体识别，目前准确度达到97%。
  网络搭建、训练全都由python实现，不依赖tensorflow，keras，pytorch等工具，为的就是能够让自己完全清楚一个神经网络搭建需要哪些步骤，每个部分是怎样设计的，以及清楚网络训练过程中前向传播，反向传播过程中具体计算方法，以及模型保存，模型调参等，本模型由三层全连接网络组成，输入层大小为784，第一层网络节点为100，第二层为100，第三层为10（这些数字在程序中都可自行设定），结构如下图所示：

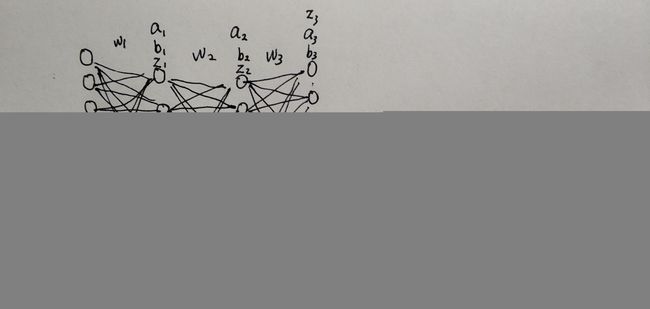
  由于本人设计的可以设置batch-size那个模型训练有点问题，所以本次介绍都是默认batch-size为1的模型，当然，如果后面我调好了我会发出来，下面我将对我模型代码一一进行讲解。

数据导入

  数据集直接调用tensorflow中keras自带的mnist数据集，也就不用我们单独下载下来了：

#加载keras内部mnist数据集
mnist=tf.keras.datasets.mnist
(train_x,train_y),(test_x,test_y)=mnist.load_data()
train_x,test_x=train_x/255,test_x/255

参数配置

#网络模型结构参数
width_input=784  #输入层神经网络节点数=28*28
width_net1=100    #第一层神经网络节点数
width_net2=100    #第二层神经网络节点数
width_net3=10    #输出层神经网络节点数
#模型训练参数
epoch=50
way_dec_lr=1     #input:1 or 2
"""学习率更新方式，选1，表示每lr_dec_epoch轮固定按lr_dec_rate比例减少学习率选择2，表示记录5次学习率大小，当当前轮次loss值大于前nub次（包括本次）loss平均值时，学习率自动降为当前学习率0.1倍，当学习率降为last_lr时，训练终止，保存模型"""
nub=3                             #设置记录nub次loss值
last_lr=0.0001              #方式2时，最终截止学习率值
learn_rate=0.01             #默认学习率
init_learn_rate=0.01                #初始学习率
lr_dec_epoch=10                #设置每10轮更新一次学习率
lr_dec_rate=0.5               #跟新学习率倍数
savepath='data/weight4.h5'     #保存模型地址
loadmodel='data/weight3.h5'    #当为迁移学习时，载入模型地址（请确保本次训练模型结构与加载的模型一致）
isretrain=False                #是否为迁移学习True or False

  可以实现神经网络模型节点数自行更改，学习率更新方式更改，是否为初始训练还是继续训练等

训练模型构建

#隐含层的激活函数def sigmoid(x):    return 1/(1+np.exp(-x))#输出层的激活函数def softmax(y):    c=np.max(y)    y=y-c    sum=np.sum(np.exp(y))    return np.exp(y)/sum#定义均方误差损失函数定义def loss(y_pre,y_grtru):    return np.sum(np.square(y_pre-y_grtru))#定义交叉熵损失函数def cross_entropy_loss(y_pre,y_grtru):    return -np.sum(y_grtru*np.log(y_pre)+(1-y_grtru)*np.log(1-y_pre))#定义网络输入层x=np.zeros((width_input,))#定义网络第一层a1=np.zeros((width_net1,))#定义网络隐藏层a2=np.zeros((width_net2,))#定义网络输出层y=np.zeros((width_net3,))
#模型权重导入def get_model(weight_path):    h5f=h5py.File(weight_path,'r')    w1=h5f['w1'][:]    b1=h5f['b1'][:]    w2=h5f['w2'][:]    b2=h5f['b2'][:]    w3=h5f['w3'][:]    b3=h5f['b3'][:]    return w1,w2,w3,b1,b2,b3#初始化模型def genarate_model():    w1=np.random.normal(0,2/width_input,(width_input,width_net1))    b1=np.random.normal(0,2/width_net1,(width_net1,))    w2=np.random.normal(0,2/width_net1,(width_net1,width_net2))    b2=np.random.normal(0,2/width_net2,(width_net2,))    w3=np.random.normal(0,2/width_net2,(width_net2,width_net3))    b3=np.random.normal(0,2/width_net3,(width_net3,))    return w1,w2,w3,b1,b2,b3#初始化nub个临时保存模型的参数,以便在早停前选取最优模型w11=np.zeros((nub,width_input,width_net1))b11=np.zeros((nub,width_net1))w21=np.zeros((nub,width_net1,width_net2))b21=np.zeros((nub,width_net2))w31=np.zeros((nub,width_net2,width_net3))b31=np.zeros((nub,width_net3))#模型参数生成if isretrain:    w1,w2,w3,b1,b2,b3=get_model(loadmodel)else:    w1,w2,w3,b1,b2,b3=genarate_model()#初始化参数z（其中a=sigmoid（z））z1=np.dot(x,w1)+b1z2=np.dot(a1,w2)+b2z3=np.dot(a2,w3)+b3#定义前向传播def feedforward(a,w,b):    return sigmoid(np.dot(a,w)+b)#保存模型def save_model(savepath,w_1,w_2,w_3,b_1,b_2,b_3):    filename=savepath    h5f=h5py.File(filename,'w')    h5f.create_dataset('w1',data=w_1)    h5f.create_dataset('w2',data=w_2)    h5f.create_dataset('w3',data=w_3)    h5f.create_dataset('b1',data=b_1)    h5f.create_dataset('b2',data=b_2)    h5f.create_dataset('b3',data=b_3)    h5f.close#初始化记录nub次loss值loss2loss2=np.zeros((nub,))#训练模型for n in range(0,epoch+1):    #方式1改变学习率    if way_dec_lr==1:        learn_rate=init_learn_rate*lr_dec_rate**(int(n/lr_dec_epoch))#学习率随着学习轮数指数递减    #打乱训练和测试样本    r=np.random.permutation(60000)    train_x = train_x[r,:,:]    train_y = train_y[r]    #r=np.random.permutation(10000)    #test_x = test_x[r,:,:]    #test_y = test_y[r]    for i in range(0,60000):        x=np.array(train_x[i])        x=x.reshape(width_input,)        z1=np.dot(x,w1)+b1        a1=feedforward(x,w1,b1)        z2=np.dot(a1,w2)+b2        a2=feedforward(a1,w2,b2)        z3=np.dot(a2,w3)+b3        #y=softmax(z3)        y=feedforward(a2,w3,b3)        y_t=np.zeros((width_net3,))        y_t[train_y[i]]=1        eta3=(-y_t/y+(1-y_t)/(1-y))*sigmoid(z3)*(1-sigmoid(z3))#此为反向传播过程中中间参数，下同        #eta3=2*(y-y_t)*sigmoid(z3)*(1-sigmoid(z3))#此为反向传播过程中中间参数，下同        eta2=np.dot(eta3,np.transpose(w3))*sigmoid(z2)*(1-sigmoid(z2))        eta1=np.dot(eta2,np.transpose(w2))*sigmoid(z1)*(1-sigmoid(z1))        b3=b3-learn_rate*eta3        b2=b2-learn_rate*eta2        b1=b1-learn_rate*eta1        w3=w3-learn_rate*np.dot(a2.reshape(width_net2,1),eta3.reshape(1,width_net3))        w2=w2-learn_rate*np.dot(a1.reshape(width_net1,1),eta2.reshape(1,width_net2))        w1=w1-learn_rate*np.dot(x.reshape(width_input,1),eta1.reshape(1,width_net1))    loss1=0    True_num=0    #加载测试集，计算loss和precition    for i in range(0,10000):        x=np.array(test_x[i])        x=x.reshape(1,width_input)        y_t=np.zeros((width_net3,))        y_t[test_y[i]]=1        a1=feedforward(x,w1,b1)        a2=feedforward(a1,w2,b2)        #z3=np.dot(a2,w3)+b3        #y=softmax(z3)        y=feedforward(a2,w3,b3)        if test_y[i]==np.argmax(y,axis=1):            True_num=True_num+1        loss1=loss1+cross_entropy_loss(y,y_t)        #loss1=loss1+loss(y,y_t)    precision=True_num/10000*100        #方式2改变学习率，利用队列方式记录连续nub次loss值    if way_dec_lr==2:        #临时存储模型        j=range(1,nub)        k=range(0,nub-1)        w11[j]=w11[k]        b11[j]=b11[k]        w21[j]=w21[k]        b21[j]=b21[k]        w31[j]=w31[k]        w11[0]=w1        b11[0]=b1        w21[0]=w2        b21[0]=b2        w31[0]=w3        b31[0]=b3        loss2[j]=loss2[k]        loss2[0]=loss1    #判断是否改变学习率        if loss2[0]>np.mean(loss2) and loss2[nub-1]>0:            learn_rate=learn_rate*0.1            if learn_rate

  上面代码由于粘贴到这发现好像不会自动换行，由于太多，实在不想一个一个enter键敲，我直接附上源码地址，直接下载吧！

训练展示

由于我自行设置了一个学习率更新方法，所以模型训练过程很快，差不多20轮左右就可以收敛，差不多10分钟左右，同时选择交叉熵损失函数也可以加快收敛，本人也发现对数据归一化处理也可以增加预测准确度：

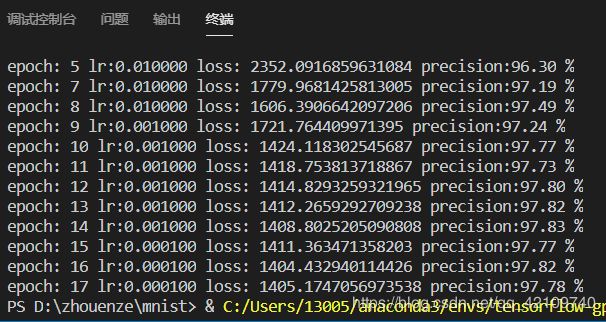
预测结果展示

方式一：直接实时手动输入测试数据编号，查看预测结果：

方式二：可以查看10000个测试数据总的准确度：

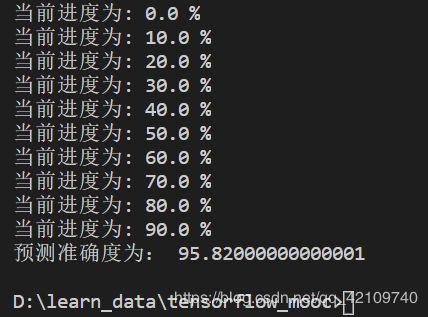
预测代码如下：

import numpy as npimport matplotlib.pyplot as pltimport h5pyimport tensorflow as tfplt.rcParams["font.family"]="SimHei"mnist=tf.keras.datasets.mnist(train_x,train_y),(test_x,test_y)=mnist.load_data()
file_path='data/weight10_2.h5' #载入训练好的模型地址def sigmoid(x):    return 1/(1+np.exp(-x))#此函数为数据集格式转换函数def data_transpose(x,y):    y_t=np.zeros((y.size,1,10))    for i in range(0,y.size):        y_t[i,0,y[i]]=1    return x.reshape(y.size,1,x[0].size),y_tdef get_model(weight_path):    h5f=h5py.File(weight_path,'r')    w1=h5f['w1'][:]    b1=h5f['b1'][:]    w2=h5f['w2'][:]    b2=h5f['b2'][:]    w3=h5f['w3'][:]    b3=h5f['b3'][:]    return w1,w2,w3,b1,b2,b3def feedforward(a,w,b):    return sigmoid(np.dot(a,w)+b)w1,w2,w3,b1,b2,b3=get_model(file_path)t_x,t_y=data_transpose(test_x,test_y)#下面这部分可以实时查看训练效果"""while True:    a=input('请输入一个0到10000的数,结束请输入‘n’：')    if a=='n':        break    a=int(a)    print('你输入的图片数字是：',test_y[a])    x=t_x[a]    a1=feedforward(x,w1,b1)    a2=feedforward(a1,w2,b2)    y=feedforward(a2,w3,b3)    print('预测结果为',np.argmax(y,axis=1))    plt.axis('off')    plt.imshow(test_x[a],cmap="gray")    plt.title("预测结果为：%d"%(np.argmax(y,axis=1)),fontsize=14)    plt.show()"""#下面部分可直接计算模型准确度True_num=0for i in range(0,10000):    x=t_x[i]    a1=feedforward(x,w1,b1)    a2=feedforward(a1,w2,b2)    y=feedforward(a2,w3,b3)    if test_y[i]==np.argmax(y,axis=1):        True_num=True_num+1    if i%1000==0:        print('当前进度为:',i/100,'%')precision=True_num/10000*100print('预测准确度为：',precision)

训练速度很快，基本上10分钟就可以收敛，同时激活函数，损失函数提供了多种，如果你使用的话，可以自行选择，有使用问题可以留言评论，我会及时回复；

原码链接：https://download.csdn.net/download/qq_42109740/12297182