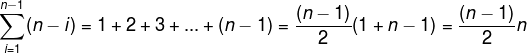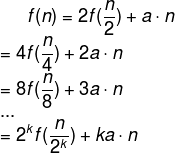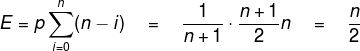算法时间复杂度的计算：从几道题目讲起

引子

最近再来回顾一下算法相关的知识，那自然，首先要学习的就是 时间复杂度的概念，以及其计算方式。下面，我就会简单地介绍下时间复杂度，以及会给出几道典型的时间复杂度计算题。

时间复杂度

将算法中基本操作的执行次数作为算法时间复杂度。

常见时间复杂度的大小比较关系：

下面，我将给出几个简单的算法，并计算其时间复杂度。

算法案例

案例一

public void fun(int n) {
    int i = 1, j = 100;
    while (i < n) {
        ++j;
        i += 2;
    }
}

求上述算法的时间复杂度。

这个算法很简单，显然问题的规模为n，基本语句为 i += 2;。我们假设循环进行了 m 次后停止。此时，我们可以得到：

1 + 2m + K = n。其中K是一个常量，可能为0，也可能为1，用于修正结果值。因为在循环结束时，i 可能等于 n，也可能等于 n-1。

上面式子最终解得：。

也就是说，上述算法的时间复杂度 T(n) = O(n)。

案例二

public void fun(int n) {
    int i, j, x = 0;
    for (i = 1; i < n; ++i) {
        for (j = i + 1; j <= n; ++j) {
            ++x;
        }
    }
}

这个算法也很简单，算法的规模为n，基本语句为 ++x;。简单的分析下，我们很容易得到：

对于每一个符合条件的 i，++x; 执行的次数为 n - (i + 1) + 1 = n - i 次。

则 ++x; 执行的总次数为：

显而易见，上述算法的时间复杂度。

案例三

public void fun(int n) {
    int i = 0, s = 0;
    while (s < n) {
        ++i;
        s += i;
    }
}

上述算法问题的规模为n，基本语句为 ++i; 和 s += i; 两句。

对于这个问题，我假设 循环经过 m 次结束，s的值为S(m)。则我们很容易得到：

• 当 m = 1 时，S(1) = 1;
• 当 m = 2 时，S(2) = S(1) + 2 = 1 + 2;
• 当 m = 3 时，S(3) = S(2) + 3 = 1 + 2 + 3;
• 由上可得：

循环经过m次后停止，此时有 S(m) + K = n。K用于修正结果。即：

我们将其解出，得到结果：

上面的是个错误值，我们直接将其舍弃。所以，该算法的基本语句执行的次数为：

显而易见，该算法的时间复杂度 。

案例四

public void mergeSort(int i, int j) {
    int m = 0;
    if (i != j) {
        m = (i + j) / 2;
        mergeSort(i, m);
        mergeSort(m + 1, j);
    }
    merge(i, j, m);
}

已知下面的条件：

• 调用该方法时，是通过 mergeSort(1, n) 来调用该方法的。
• merge() 方法的时间复杂度为 O(n)。

求 该算法的时间复杂度。

首先，我们来理解一下该方法。该方法实际的逻辑可以理解是，将需要排序的集合二等分为两份，分别进行排序。

比如，假设我们给定一个例子，i = 1，j = 20，意味着我们将对一个含有20个元素的集合进行排序。在 mergeSort() 方法中，会将该集合分为两个集合，第一个集合是 下标从1到10，第二个集合是下标从 11到20。所以，如果我们设定 mergeSort() 方法的基本操作次数为 f(n)，则 mergeSort() 方法内部的 mergeSort() 方法的基本操作次数就是 。

有了上面的理解，我们就能够进行推理：

已知 merge() 方法的时间复杂度为 O(n)，我们假设 merge() 方法的基本操作次数为 a·n。

我们假设mergeSort()方法的基本操作次数为 f(n)。我们可以得出：

   ①；

当  时，代入①式有：

    ②；

将 ② 式带入 ① 式，得到：

   ③；

又有当 时，代入①式有：

       ④；

将 ④ 式带入 ③ 式，得到：

    ⑤；

同样，我们分别再求、...、，综合上面①、③、⑤式，可以得到：

也就是说，      ⑥。

然后，从 mergeSort() 方法我们可以得出  f(1) = O(1)     ⑦  。

这里，根据 ⑦ 式，我们想办法化掉 ，则当  时，有

这里，两个式子结合，替换掉k，则可以得到mergeSort()方法的基本操作次数为：

显然，mergeSort()方法的时间复杂度 。

案例五

具有 n 个元素的顺序表，如上图，分析其插入和删除一个元素的时间复杂度。

对于上面这个顺序表，假设其是一个数组。我们分析其插入一个元素时，需要移动元素的平均个数。这里，我们分两步进行分析：

首先，求概率。

总有 n 个元素，则其总共有 n + 1 个插入点。每个位置被插入的可能性相同，则每一个未知被插入概率为：。

然后，求元素移动个数。

假设要把新元素插入到第 i 个元素之后（如果在1号元素之前插入，则记做在 0 号元素之后插入），则需要将第 i 号元素之后的所有元素向后移动1位，移动元素的个数为：n - i 。

所以，移动元素个数的期望为：

显然，平均要移动一半的元素，插入算法的时间复杂度T(n) = O(n)，删除算法也是一样为O(n)。

总结

算法是程序员的内功心法，而时间复杂度又是算法学习的基石。时间复杂度的计算牵涉到的数学知识很多，准备最近赶紧复习一下数学了~

参考文章

1、《数据结构高分笔记》2016版，率辉 主编。