第七章 支持向量机（一）线性可分支持向量机与硬间隔最大化

模型： 二类分类模型
3种支持向量机模型
线性可分支持向量机：硬间隔最大化+线性分类器
线性支持向量机：软间隔最大化+线性分类器
非线性支持向量机：核技巧+软间隔最大化
策略：形式化为求解凸二次规划问题
算法： 求解凸二次规划的最优化算法

线性可分支持向量机与硬间隔最大化

训练数据集 D={(x1,y1),(x2,y2)...(xn,yn)} D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . ( x n , y n ) }
xi∈Rn,yi∈{+1,−1} x i ∈ R n , y i ∈ { + 1 , − 1 }

f(x)=sign(w⋅x+b) f ( x ) = s i g n ( w ⋅ x + b )

参数 w,b w , b 。
和感知机一样，学习的目标是在特征空间中寻找一个分离超平面。
感知机的策略是：误分类最小，解不唯一
线性可分SVM：间隔最大化，解唯一

一、 函数间隔与几何间隔

样本的函数间隔

γi^=yi(w⋅xi+b) γ i ^ = y i ( w ⋅ x i + b )

训练集的函数间隔

γ^=mini=1,...nγi^ γ ^ = m i n i = 1 , . . . n ⁡ γ i ^

函数间隔可以表示分类预测的正确性及确信度
符号为正表示分类正确；反之错误
数值越小，表示离超平面越近，该点的预测就不那么确信。
成比例的改变 w,b w , b ,超平面不变，函数间隔成倍的改变
样本的几何间隔

γi=yi(w||w||⋅xi+b||w||) γ i = y i ( w | | w | | ⋅ x i + b | | w | | )

训练集的几何间隔

γ=mini=1,...nγi γ = m i n i = 1 , . . . n ⁡ γ i

函数间隔和几何间隔的关系

γi=γi^||w|| γ i = γ i ^ | | w | |

γ=γ^||w|| γ = γ ^ | | w | |

几何间隔是有符号的，分类正确时才等于点到超平面的距离

二、硬间隔最大化

感知机中有无数的分离超平面，而哪一个才是最好的（泛化能力最强）？
SVM直观想法：离超平面最近的点尽可能的远离超平面
我们最关心的的是离超平面最近的点（最难分的点），如果超平面有足够大的确信度将他们分开，这个超平面应该对未知的新实例有很好的分类预测能力。
几何间隔最大的分离超平面可以表示为下面的约束最优化问题

maxw,bγ m a x w , b γ

s.t.yi(w||w||⋅xi+b||w||)≥γ,i=1,2,..n s . t . y i ( w | | w | | ⋅ x i + b | | w | | ) ≥ γ , i = 1 , 2 , . . n

由函数间隔和几何间隔的关系，得

maxw,bγ^||w|| m a x w , b γ ^ | | w | |

s.t.yi(w⋅xi+b)≥γ^,i=1,2,..n s . t . y i ( w ⋅ x i + b ) ≥ γ ^ , i = 1 , 2 , . . n

缩放超平面的参数，函数间隔的取值是可以任意改变的，因此将最小的函数间隔取为1（ γ^=1 γ ^ = 1 ）
最大化 1||w|| 1 | | w | | 等价于最小化 12||w||2 1 2 | | w | | 2
线性可分支持向量机的最优化问题为

minw,b12||w||2(1) (1) m i n w , b 1 2 | | w | | 2

s.t.−yi(w⋅xi+b)+1≤0,i=1,2,..n(2) (2) s . t . − y i ( w ⋅ x i + b ) + 1 ≤ 0 , i = 1 , 2 , . . n

三、支持向量与间隔边界

支持向量： 训练集中离超平面最近的点（是使约束条件等号成立的点）
超平面 w⋅x+b=+1 w ⋅ x + b = + 1 和 w⋅x+b=−1 w ⋅ x + b = − 1 称为间隔边界。

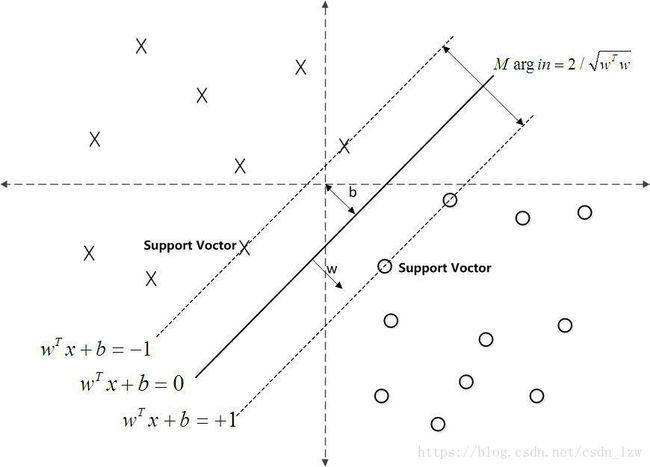
在决定超平面时只有支持向量其作用。如果移动支持向量将改变所求解，但是如果在间隔边界以外移动其他点，甚至删去这些点，则解是不会改变的。

四、对偶算法

这部分需要先了解拉格朗日对偶，以下表述有部分不严谨

4.1、对偶算法一般步骤

1.把约束优化问题写成规范的原始问题（规范的原始问题的目标函数是最小化问题，不等式约束是小于等于）
2.引入拉格朗日乘子，构建拉格朗日函数L
3.求解对偶问题的解，L的极大极小问题，（先极小求偏导，再极大用SMO算法）
4.根据KKT条件得到原始问题解和对偶问题解的关系。

4.2、线性可分SVM应用对偶算法

1.公式（1）（2）已经是规范的原始问题
2.构建拉格朗日函数（引入拉格朗日乘子 αi≥0,i=1,2...n α i ≥ 0 , i = 1 , 2... n ，把约束问题写成无约束）

L(w,b,α)=12||w||2−∑i=1nαiyi(w⋅xi+b)+∑i=1nαi L ( w , b , α ) = 1 2 | | w | | 2 − ∑ i = 1 n α i y i ( w ⋅ x i + b ) + ∑ i = 1 n α i

3.原始问题的解等价于先求拉格朗日函数对 α α 求极大，再对 w,b w , b 求极小。解是 w,b w , b 。
原始问题 = L的极小极大问题
对偶问题的解等价于先求拉格朗日函数对 w,b w , b 求极小，再对 α α 求极大。解是 α α 。
对偶问题 = L的极大极小问题

maxαminw,bL(w,b,α) m a x α ⁡ m i n w , b ⁡ L ( w , b , α )

(1) 求 minw,bL(w,b,α) m i n w , b ⁡ L ( w , b , α )
公式敲不动了，手写字真丑ヽ(｀Д´)ﾉ︵ ┻━┻ ┻━┻

通过求导和回代就得到了

minw,bL(w,b,α)=−12∑i=1n∑j=1nαiαjyiyj(xi⋅xj)+∑i=1nαi m i n w , b ⁡ L ( w , b , α ) = − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 n α i

(2) 求 minw,bL(w,b,α) m i n w , b ⁡ L ( w , b , α ) 对 α α 的极大,即对偶问题

maxα−12∑i=1n∑j=1nαiαjyiyj(xi⋅xj)+∑i=1nαi(3) (3) m a x α − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 n α i

s.t.∑i=1nαiyi=0(4) (4) s . t . ∑ i = 1 n α i y i = 0

αi≥0,i=1,2,...n(5) (5) α i ≥ 0 , i = 1 , 2 , . . . n

对偶问题的解公式（3）-（5），可以通过SMO算法求解得到
4.原始问题解和对偶问题解的关系。
定理：目标函数和不等式约束是凸函数，等式约束是仿射函数，不等式约束是严格可执行的。
则 w,b w , b 和 α α 是原始问题和对偶问题的解的充要条件是 w,b w , b 和 α α 满足KKT条件。
KKT条件：
1.解的偏导=0，
2.解满足不等式约束，
3.解满足等式约束，
4.拉格朗日乘子大于等于0，
5. 对偶互补条件：拉格朗日乘子大于0时，解的不等式约束的等号成立
线性可分支持向量机的KKT条件

∇wL(w∗,b∗,α∗)=w∗−∑i=1nα∗iyixi=0 ∇ w L ( w ∗ , b ∗ , α ∗ ) = w ∗ − ∑ i = 1 n α i ∗ y i x i = 0

∇bL(w∗,b∗,α∗)=−∑i=1nα∗iyi=0 ∇ b L ( w ∗ , b ∗ , α ∗ ) = − ∑ i = 1 n α i ∗ y i = 0

yi(w∗⋅xi+b∗)−1≥0,i=1,2,...n y i ( w ∗ ⋅ x i + b ∗ ) − 1 ≥ 0 , i = 1 , 2 , . . . n

α∗i≥0,i=1,2,...n α i ∗ ≥ 0 , i = 1 , 2 , . . . n

α∗i(yi(w∗⋅xi+b∗)−1)=0,i=1,2,...n α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 ) = 0 , i = 1 , 2 , . . . n

由第一个偏导得到

w∗=∑iα∗iyixi(6) (6) w ∗ = ∑ i α i ∗ y i x i

参数 b b 是根据对偶互补条件得到的。
如果每个 α α 都等于0,那么 w∗=0 w ∗ = 0 ,w^*=0不是原问题的解。所以至少有一个 α>0 α > 0
设存在下标 j j ,使得 α∗j>0 α j ∗ > 0 ,互补条件知

yj(w∗⋅xj+b∗)−1=0 y j ( w ∗ ⋅ x j + b ∗ ) − 1 = 0

y2j=1 y j 2 = 1 得

b∗=yj−∑i=1nα∗iyi(xi⋅xj)(7) (7) b ∗ = y j − ∑ i = 1 n α i ∗ y i ( x i ⋅ x j )

由公式（6）（7）知， w∗，b∗ w ∗ ， b ∗ 只依赖于训练数据集中 α∗>0 α ∗ > 0 的样本点（称这样的点为支持向量），而其他样本点对 w∗，b∗ w ∗ ， b ∗ 没有影响。
根据互补条件知 α∗>0 α ∗ > 0 时

yj(w∗⋅xj+b∗)=1 y j ( w ∗ ⋅ x j + b ∗ ) = 1

样本的函数间隔为1，这与之前定义的支持向量是一致的。
疑问？？
1. 为什么KKT条件没有对 α α 求偏导
2. KKT条件中对b求偏导得到的公式，说明支持向量是成对的？
3. b的取值有多个吗？超平面不是唯一的吗