神奇的Gamma函数(scipy)
Γ(x)=∫∞0tx−1e−tdt
对应于scipy(python库)的:
from scipy.special import gamma通过分布积分的方法,进行如下的推导:
Γ(x+1)=∫∞0txe−tdt=−∫∞0txd(e−t)=−[txe−t|∞0−x∫∞0tx−1e−tdt]=xΓ(x)
可得该函数如下的递归性质:
Γ(x+1)=xΓ(x)
>>> gamma(5+1)
120.0
>>> 5*gamma(5)
120.0于是很容易证明( Γ(1)=1,Γ(n)=(n−1)Γ(n−1) ), Γ(x) 函数可以看成是阶乘在实数集上的延拓,具有如下的性质:
Γ(n)=(n−1)!
Γ(n) 与 B(m,n) 的关系
B(m,n)=∫10xm−1(1−x)n−1dxB(m,n)=Γ(m)Γ(n)Γ(m+n)
从二项分布到 Gamma 分布
对Gamma 函数的定义稍作变形,可得如下等式:
∫∞0xα−1e−xΓ(α)dx=1
于是 取积分中的函数作为概率密度(Probability Density Function,PDF),就得到一个形式最为简单的Gamma 分布的密度函数(density function):
Gamma(x|α)=xα−1e−xΓ(α)
如果再做一个变换 x=βt ,就得Gamma 分布的更一般形式:
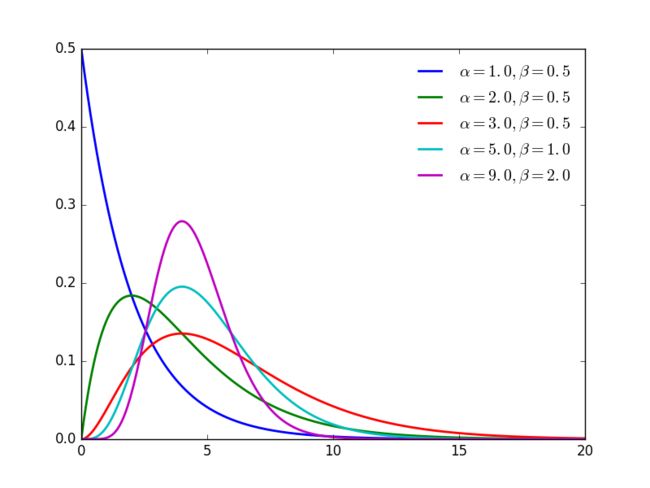
Gamma(t|α,β)=βαtα−1e−βtΓ(α)
其中 α 称为形状参数(shape parameter),主要决定了分布曲线的形状,而 β 称为 rate parameter(或叫 inverse scale parameter, 1β 称为scale parameter),主要决定曲线有多陡。
Gamma 分布与Possion 分布
Gamma 分布首先与Possion 分布(离散型)、Possion 过程发生密切的联系。我们容易发现Gamma分布的概率密度和Possion分布在数学形式具有高度的一致性。参数为 λ 的Possion分布,其概率(probability mass function,pmf)为:
Possion(X=k|λ)=λke−λk!
而Gamma分布的密度( α=k+1,β=1 )得到:
Gamma(x|α=k+1)=xαe−xΓ(k+1)=xke−xk!
所以这两个分布在数学形式上是一致的,只是Possion分布是离散的,Gamma分布是连续的, 可以直观地认为Gamma分布是Possion分布在正实数集上的连续化版本。
我们在概率论与数理统计的课程中都学过, Poisson(λ) 分布可以看成是二项分布 B(n,p) 在 np=λ,n→∞ 条件下的极限分布:
B(k;n,p)=(nk)pk(1−p)n−k⟶np=λ,n→∞Poisson(X=k|np)=λke−λk!
如果你对二项分布的关注足够多,可能会知道二项分布的随机变量 X B(n,p) 满足下面一个奇妙的 恒等式:
P(X≤k)=n!k!(n−k−1)!∫1ptk(1−t)n−k−1dt
我们在等式右侧做一个变换 t=xn 可得:
P(X≤k)=====n!k!(n−k−1)!∫nnp(xn)k(1−xn)n−k−1d(xn)∫nnp(n−1)!k!(n−k−1)!(xn)k(1−xn)n−k−1dx∫nnp(n−1k)(xn)k(1−xn)n−k−1dx∫nnpB(k;n−1,xn)dx∫nnpB(Y=k|n−1,xn)dx
上式左侧是二项分布 B(n,p) 的累积分布函数(cumulative density function,cdf),而右侧为无穷多个二项分布 B(n−1,xn) 的积分和,所以可以写为:
B(X≤k|n,p)=∫nnpB(Y=k|n−1,xn)dx
对上式两边在条件 np=λ,n→∞ 下取极限,则得到:
Poisson(X≤k|λ)=∫∞λPoisson(Y=k|x)dx=∫∞λxke−xk!dx
到这,不妨先暂停,我们使用scipy做一个简单验证:
import scipy.stats as st
from scipy.misc import factorial
from scipy import integrate
lmbda, k = 2, 6
X = st.poisson(2)
# X ~ Poisson(2)
print(X.cdf(k))
# P(X<=k)
def poisson_pdf(x, k):
return x**k*np.exp(-x)/factorial(k)
print(integrate.quad(possion_pdf, lmbda, np.inf, args=(k))[0])
# 0.995466194474
# 0.9954661944737513
# 两者达到完美的相等书归正传,我们再来看上面的公式,
Poisson(X≤k|λ)=∫∞λPoisson(Y=k|x)dx=∫∞λxke−xk!dx
该等式即为著名的 Poisson-Gamma duality,接下来我们来点好玩的,对上面的等式两边在 λ→0 取极限,左侧Poisson分布表示的是至少发生 k 事件的概率, λ→0 的时候就不可能有事件再发生了,故 P(X≤k)=0 ,于是:
1=limλ→0∫∞λxke−xk!dx=∫∞0xke−xk!dx
该积分式子说明 f(x)=xke−xk! 在实数集上是一个概率分布函数(probability density function,pdf),而这个函数恰好就是 Gamma分布( Gamma(x|α)=xα−1e−xΓ(α),α=k+1 )( 也即我们通过二项分布,再根据泊松定理,推导出了最后的Gamma分布)。我们继续把上式右边中的 k! 移到左边,于是得到:
k!=∫∞0xke−xdx
于是我们得到了将 k! 表示为积分(也即从此我们可以计算3.5的阶乘了)的方法。
好吧,文章已经够长的了,公式已经够繁复的了,下文,我们将重点实现阶乘在正实数轴上的连续化(或者叫插值),其实已经很明显了。