java数据结构和算法——递归实现迷宫回溯问题的应用示例
一、迷宫回溯示例要求：
- 定义一个8行7列的迷宫地图，得到小球从起始位置到结束位置的路径
- 需求示意图如下
二、使用递归回溯来给小球找路，按照 下->右->上->左 的策略(方法)的示例
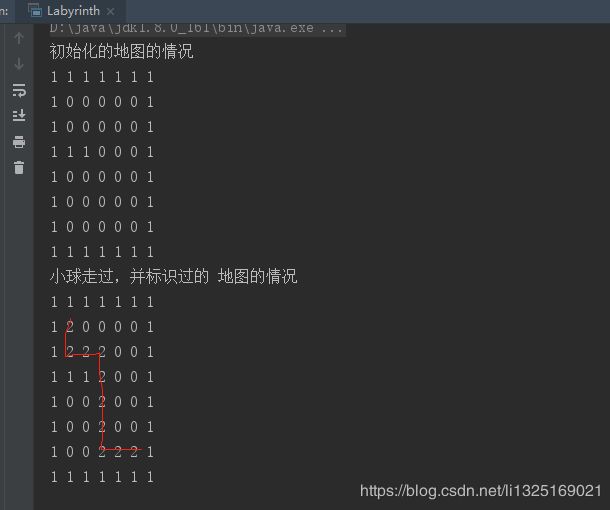
1、按照 下->右->上->左 的策略，小球行走的路径示意图如下：
2、按照 下->右->上->左 的策略，示例代码
package com.rf.springboot01.dataStructure.recursion;
/**
* @description: 使用递归实现迷宫问题
* @author: xiaozhi
* @create: 2020-07-30 16:05
*/
public class Labyrinth {
public static void main(String[] args) {
//定义一个8行7列的二维数组，模拟迷宫地图
int[][] map =new int[8][7];
//1 表示墙，0：表示空地
for(int i=0;i<7;i++){//遍历列数，每一列的第一行和第8行填充数字1
map[0][i]=1;//第1行填充数字1，模拟地图的墙
map[7][i]=1;//第8行填充数字1，模拟地图的墙
}
for(int j=0;j<8;j++){//遍历行数，每一行的第一列和第7列填充数字1
map[j][0]=1;//第1列填充数字1，模拟地图的墙
map[j][6]=1;//第7列填充数字1，模拟地图的墙
}
//模拟中间的挡墙，第4行第2列和第4行第3列，填充数字1
map[3][1]=1;
map[3][2]=1;
//输出二维数组模拟的迷宫地图
System.out.println("初始化的地图的情况");
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+ " ");
}
System.out.println();
}
//使用递归回溯给小球找路，按照 下->右->上->左 的策略(方法)
setWay(map,1,1);
//输出新的地图, 小球走过，并标识过的递归
System.out.println("小球走过，并标识过的 地图的情况");
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
/**
* @Description: 使用递归回溯来给小球找路，按照 下->右->上->左 的策略(方法)
* 说明:1、map 表示地图
* 2. i,j 表示从地图的哪个位置开始出发 (1,1)
* 3、如果小球能到 map[6][5] 位置，则说明通路找到.
* 4、约定： 当map[i][j] =0 表示该点没有走过
* 当map[i][j] =1 表示墙
* 当map[i][j] =2 表示通路可以走
* 当map[i][j] =3 表示该点已经走过，但是走不通
* 5、确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
* @Param:
* @Author: xz
* @return: 如果找到通路，就返回true, 否则返回false
* @Date: 2020/7/31 8:51
*/
public static boolean setWay(int[][] map, int i, int j) {
if(map[6][5]==2){//已到达终点位置，通路已找到
return true;
}else{
if(map[i][j]==0){//如果当前这个点还没有走过,按照策略 下->右->上->左 走
map[i][j]=2;// 假定该点是可以走通.
if(setWay(map,i+1,j)){//向下走
return true;
}else if(setWay(map,i,j+1)){//向右走
return true;
}else if(setWay(map,i-1,j)){//向上走
return true;
}else if(setWay(map,i,j-1)){//向左走
return true;
}else{//说明该点是走不通，是死路
map[i][j]=3;
return false;
}
}else{// 如果map[i][j] != 0 , 可能是 1， 2， 3
return false;
}
}
}
}
3、运行main函数，结果如下：和步骤1中的示意图完全相同
三、使用递归回溯来给小球找路，按照 上->右->下->左的策略(方法)的示例
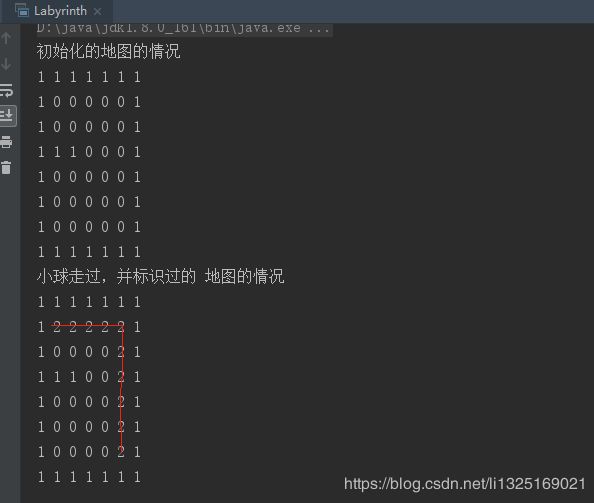
1、按照上->右->下->左 的策略，小球行走的路径示意图如下：
2、按照上->右->下->左 的策略，示例代码
package com.rf.springboot01.dataStructure.recursion;
/**
* @description: 使用递归实现迷宫问题
* @author: xiaozhi
* @create: 2020-07-30 16:05
*/
public class Labyrinth {
public static void main(String[] args) {
//定义一个8行7列的二维数组，模拟迷宫地图
int[][] map =new int[8][7];
//1 表示墙，0：表示空地
for(int i=0;i<7;i++){//遍历列数，每一列的第一行和第8行填充数字1
map[0][i]=1;//第1行填充数字1，模拟地图的墙
map[7][i]=1;//第8行填充数字1，模拟地图的墙
}
for(int j=0;j<8;j++){//遍历行数，每一行的第一列和第7列填充数字1
map[j][0]=1;//第1列填充数字1，模拟地图的墙
map[j][6]=1;//第7列填充数字1，模拟地图的墙
}
//模拟中间的挡墙，第4行第2列和第4行第3列，填充数字1
map[3][1]=1;
map[3][2]=1;
//输出二维数组模拟的迷宫地图
System.out.println("初始化的地图的情况");
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+ " ");
}
System.out.println();
}
//使用递归回溯给小球找路，按照 上->右->下->左 的策略(方法)
setWay2(map,1,1);
//输出新的地图, 小球走过，并标识过的递归
System.out.println("小球走过，并标识过的 地图的情况");
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
/**
* @Description: 使用递归回溯来给小球找路，按照 上->右->下->左 的策略(方法)
* 说明:1、map 表示地图
* 2. i,j 表示从地图的哪个位置开始出发 (1,1)
* 3、如果小球能到 map[6][5] 位置，则说明通路找到.
* 4、约定： 当map[i][j] =0 表示该点没有走过
* 当map[i][j] =1 表示墙
* 当map[i][j] =2 表示通路可以走
* 当map[i][j] =3 表示该点已经走过，但是走不通
* 5、确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
* @Param:
* @Author: xz
* @return: 如果找到通路，就返回true, 否则返回false
* @Date: 2020/7/31 8:51
*/
public static boolean setWay2(int[][] map, int i, int j) {
if(map[6][5]==2){//已到达终点位置，通路已找到
return true;
}else{
if(map[i][j]==0){//如果当前这个点还没有走过,按照策略 上->右->下->左
map[i][j]=2;// 假定该点是可以走通.
if(setWay2(map,i-1,j)){//向上走
return true;
}else if(setWay2(map,i,j+1)){//向右走
return true;
}else if(setWay2(map,i+1,j)){//向下走
return true;
}else if(setWay2(map,i,j-1)){//向左走
return true;
}else{//说明该点是走不通，是死路
map[i][j]=3;
return false;
}
}else{// 如果map[i][j] != 0 , 可能是 1， 2， 3
return false;
}
}
}
}
3、运行main函数，结果如下：和步骤1中的示意图完全相同
三、使用递归回溯来给小球找路，展示回溯问题示例
1、回溯问题示意图如下
2、回溯问题示例代码如下
package com.rf.springboot01.dataStructure.recursion;
/**
* @description: 使用递归实现迷宫问题
* @author: xiaozhi
* @create: 2020-07-30 16:05
*/
public class Labyrinth {
public static void main(String[] args) {
//定义一个8行7列的二维数组，模拟迷宫地图
int[][] map =new int[8][7];
//1 表示墙，0：表示空地
for(int i=0;i<7;i++){//遍历列数，每一列的第一行和第8行填充数字1
map[0][i]=1;//第1行填充数字1，模拟地图的墙
map[7][i]=1;//第8行填充数字1，模拟地图的墙
}
for(int j=0;j<8;j++){//遍历行数，每一行的第一列和第7列填充数字1
map[j][0]=1;//第1列填充数字1，模拟地图的墙
map[j][6]=1;//第7列填充数字1，模拟地图的墙
}
//模拟中间的挡墙，第4行第2列和第4行第3列，填充数字1
map[3][1]=1;
map[3][2]=1;
map[1][2]=1;
map[2][2]=1;
//输出二维数组模拟的迷宫地图
System.out.println("初始化的地图的情况");
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+ " ");
}
System.out.println();
}
//使用递归回溯给小球找路，按照 下->右->上->左 的策略(方法)
setWay(map,1,1);
//输出新的地图, 小球走过，并标识过的递归
System.out.println("小球走过，并标识过的 地图的情况");
for(int i=0;i<8;i++){
for(int j=0;j<7;j++){
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
/**
* @Description: 使用递归回溯来给小球找路，按照 下->右->上->左 的策略(方法)
* 说明:1、map 表示地图
* 2. i,j 表示从地图的哪个位置开始出发 (1,1)
* 3、如果小球能到 map[6][5] 位置，则说明通路找到.
* 4、约定： 当map[i][j] =0 表示该点没有走过
* 当map[i][j] =1 表示墙
* 当map[i][j] =2 表示通路可以走
* 当map[i][j] =3 表示该点已经走过，但是走不通
* 5、确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
* @Param:
* @Author: xz
* @return: 如果找到通路，就返回true, 否则返回false
* @Date: 2020/7/31 8:51
*/
public static boolean setWay(int[][] map, int i, int j) {
if(map[6][5]==2){//已到达终点位置，通路已找到
return true;
}else{
if(map[i][j]==0){//如果当前这个点还没有走过,按照策略 下->右->上->左 走
map[i][j]=2;// 假定该点是可以走通.
if(setWay(map,i+1,j)){//向下走
return true;
}else if(setWay(map,i,j+1)){//向右走
return true;
}else if(setWay(map,i-1,j)){//向上走
return true;
}else if(setWay(map,i,j-1)){//向左走
return true;
}else{//说明该点是走不通，是死路
map[i][j]=3;
return false;
}
}else{// 如果map[i][j] != 0 , 可能是 1， 2， 3
return false;
}
}
}
}
3、运行main函数，结果如下：和步骤1中的示意图完全相同
