pytorch实现kaggle手写数字识别

手写数字识别实验报告

一、实验介绍

这是个分类问题，可以用传统的机器学习，例如决策树、SVM等等方法，深度学习的火热，当然是选择加入它了。

在本次实验中，本人先实现了一个lenet5的版本，而且未进行任何优化，防止过拟合等的操作，在第一次提交的时候，达到了0.97742的分数。随后了解到每个输入的像素点的值在0-255之间，进行除以255的操作后再次提交，分数达到0.98371。在下一次的提交版本中，加入了BN层以及dropout层，成绩得到了提高，0.99028。最后一次提交，将lenet5中的5\*5卷积换成了两个3\*3的卷积，采用类似VGG的改进，最终提交版本为0.99414的得分。

二、实验过程

1、数据预处理

traindata_pd = pd.read_csv("./data/train.csv")
traindata_x_np = (traindata_pd.to_numpy()[:, 1:].reshape(-1, 1, 28, 28) / 255.0 - 0.5) / 0.5
traindata_y_np = traindata_pd.to_numpy()[:, 0].astype(int)
traindata_x_t = torch.from_numpy(traindata_x_np).float()
traindata_y_t = torch.from_numpy(traindata_y_np).long()
traindata = TensorDataset(traindata_x_t, traindata_y_t)
train_size = int(0.8 * len(traindata))
valid_size = len(traindata) - train_size
# train_dataset = traindata
train_dataset, valid_dataset = torch.utils.data.random_split(traindata, [train_size, valid_size])

testdata_pd = pd.read_csv("./data/test.csv")
testdata_t = torch.from_numpy(((testdata_pd.to_numpy().reshape(-1, 1, 28, 28) / 255.0) - 0.5) / 0.5).float()
testdata = TensorDataset(testdata_t)

​  在第一次提交的时候，我没有进行归一化，使数据分布在-1到1之间，效果不是很好。随后我进行了正态分布归一化。进行归一化后带来了比较大的提升，可以降低梯度计算的复杂性，加快网络的收敛，还能统一量纲（例如某一特征的范围是在0到1e-6，而有的特征在0到1e6，本人专业上电路设计优化就存在这样的情况）。除此之外，还将训练集留出1/5大小作为验证集，用于评估模型好坏。

​  在翻阅kaggle中的NoteBook发现，别人提到了数据增强的手段，尝试使用后发现迭代速度变慢了，而且未看到明显效果，可能自己使用有误，而且对这一优化手段的代码不是很熟，最后并未使用（似乎要用上torchvision库中的transforms）。

2、模型的设计与选择

 在这一环节中，由于要求使用多个baseline，在此还实现了MLP以及LSTM，CNN方面则实现了lenet5和Vgg。

（1）MLP即多层感知机，或全连接神经网络

 网络结构大体如上图，是一个三层网络，在本人实验中选择的是第一个隐藏层120节点，第二个隐藏层84个节点，输出层10个节点。和lenet5最后的全连接层采用一样的结构。最终在训练集中取得了0.988的准确率，在验证集为0.979的准确率。

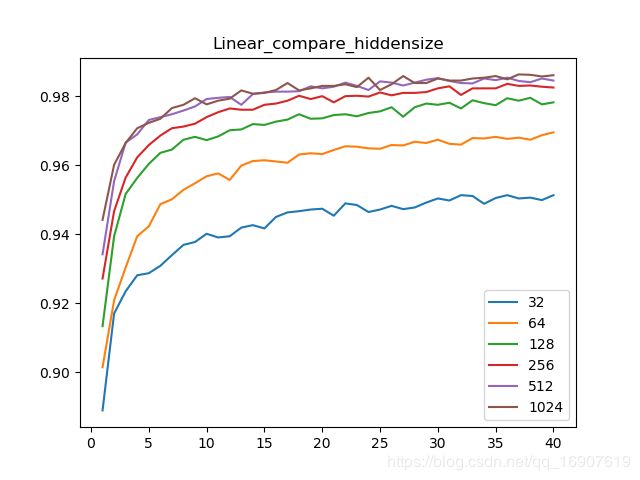
 在进一步的探索中，我对全连接层的第一个隐藏层的节点个数进行了探索，以32到1024之间取了六种数值训练网络，看在验证集上的表现。

 其中参数个数为:

$num_params=hiddensize \times 28 \times 28 +hiddensize + 84 \times hiddensize + 84 + 10 \times 84 + 10 $

即$469\times hiddensize+938$，对于$$hiddensize=128$$，$$num\_params=60790$$

 准确率如下图：

 可以发现，对于全连接网络增加节点数量对网络的性能提升有非常明显的影响，不过可以发现512节点与1024个时候变化并不大，也就是说并不是一味得增加节点数量就可以提高性能。个人认为，增加全连接层节点数带来性能提升的原因是，增强了拟合能力，但同时也带来了过拟合风险，但网络过于简单，最后并没继续上升，相反可能下降，而且节点数过多会使训练速度变慢。

 在1024节点的时候，MLP网络达到的最大验证集准确率为0.9863。

（2）RNN循环神经网络与LSTM

 RNN网络的理解花费了一定的时间。如上图，可以认为它有四个单层的神经网络，这四个神经网络一模一样，共享一样的权值，但前一个的输出会对后一个的输出有影响。在没有相互联系的情况，应该有这个单层网络是这样的输出形式：$$h^{(t)}=\Phi (U{x}^{(t)}+b)$$。而RNN网络在该时刻的输出与之前的状态有关，变成了$$h^{(t)}=\Phi (U{x}^{(t)}+W{h}^{(t-1)}+b)$$。这是单层的情况，可以将每个输出又作为下一层的输入，实现多层RNN的连接。

 LSTM就是RNN的进化版，结构还是和RNN一样，只是每个cell里面更加地复杂了，原来的RNN只具有短时记忆，而RNN增加了三个门，具有选择的作用，实现长短记忆，门的细节尚未仔细研究。

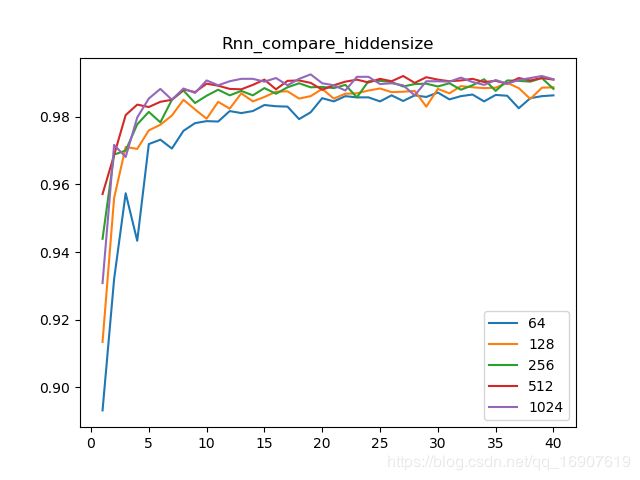
 接下来是将LSTM用于本次实验中，一开始一直没搞清楚怎么处理序列的问题，后来得知可以将$$28\times 28$$的输入看成是一个序列，序列大小为28个，每个输入为28维的向量。在本次实验中，我所用的LSTM是个两层的结构，隐藏层单元个数为可变，设置了64,128,256,512,1024共五个值进行比较。参数个数为：

$$num\_params=gates\times [(28+hiddensize)\times hiddensize+hiddensize+$$

​ $$(hiddensize+hiddensize)\times hiddensize+hiddensize]+hiddensize\times 10+10$$

 LSTM的门数量为4，可以算出对于隐层单元为64的情况，$$nums\_params=57482$$

 从图像来看，也有随隐层单元数增加而准确度上升的现象，但不太明显。基于两层LSTM的模型，最终准确率可以达到0.9917

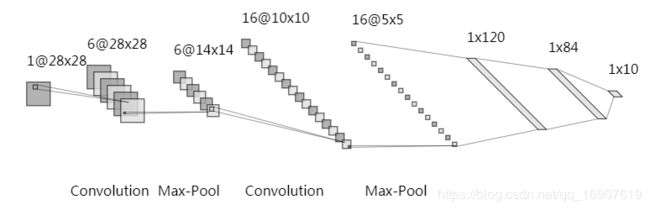
（3）LeNet5

 轮到LeNet5模型，基本和LeNet5结构一样，除了第一层使用了padding=2填充，实现这一网络时有几点收获：一是BatchNorm层，效果很好，不过原理还没吃透；二是关于池化层与卷积层以及激活层之间的顺序，看各种经典结构池化层是位于激活层后面，卷积层前面，而在我的实验中，我将它放在了激活层的前面卷积层后面。发现不会有影响，在我看来，这两个操作都是独立的不区分先后顺序的，因此可以交换，而且交换之后，个人觉得可以减少激活层的计算量，提高效率；三，在优化这个网络的时候，用上了Dropout层，也对准确率起了很大的作用，这个在后面再提。

 第一层卷积通道数为32时，模型参数：

$$num\_params=1\times 5\times 5\times 32+32\times 5\times 5\times 16+16\times 5\times 5\times 120+120+120\times 84$$

$$+84+84\times 10+10=72734$$

 这个网络中，我探索了第一层卷积通道数对准确率的影响。如下图：

 可以看出当第一层卷积的通道数是32的时候，在验证集上的效果更好。

（4）VGG类型的网络

 由于VGGnet提出了新的思路，将神经网络往使网络更深的方向发展，当中提出可以用两个$$3\times 3$$的卷积核代替一个$$5\times 5$$的卷积核。于是将这一思路用在了改善lenet5上，于是网络结构变成了如上图所示，这一次，我仍然是探究了第一层的卷积的通道数对模型的影响。有下图的结果：

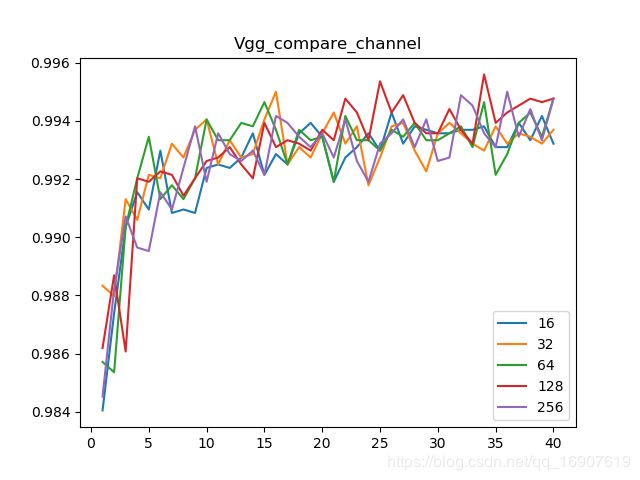
 第一层通道数在128的时候效果比较好。

 通道为128时，参数个数为：

$$num\_params=1\times 3\times 3\times 128+128\times 3\times 3\times 128+128\times 3\times 3\times 32+32\times 3\times 3\times 32$$

$$+7\times 7\times 32\times 120+120+120\times 84+84+84\times 10+10=393982$$

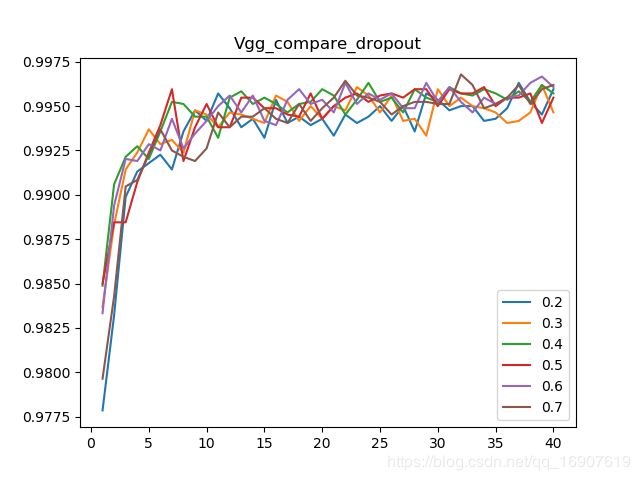
 随后对于在128的情况下的dropout概率进行了探究：

 发现dropout概率取值在0.2到0.7似乎都不差，其中绿色线似乎更平稳些，也就是0.4

3、训练并评估模型

class MnistClassfier(object):
    def __init__(self, netname, cnnpara=None, linearpara=None, rnnpara=None, dropout=0, lr=0.003):
        self.usecuda = torch.cuda.is_available()
        self.model = None
        if netname == 'LeNet' or netname == 'Vgg':
            self.model = MnistCNN(netname, cnnpara, linearpara, dropout=dropout)
        elif netname == 'Linear':
            self.model = MnistMLP(linearpara, dropout=dropout)
        elif netname == 'Rnn':
            self.model = MnistLSTM(rnnpara, dropout=dropout)
        else:
            self.model = MnistMLP((64, 64), dropout=0)
        print(self.model)
        self.criterion = nn.CrossEntropyLoss()
        if self.usecuda:
            self.model.cuda()
            self.model = torch.nn.DataParallel(self.model,device_ids=range(torch.cuda.device_count()))
            cudnn.benchmark = True
            self.criterion = self.criterion.cuda()
        self.optimizer = optim.Adam(self.model.parameters(), lr=lr, betas=(0.9, 0.99))
        # self.optimizer=optim.RMSprop(self.model.parameters(),lr=lr,alpha=0.9,momentum=0.9, weight_decay=5e-4)

    def train(self, traindataset, batch_size, epoch):
        self.model.train()
        trainLoader = DataLoader(dataset=traindataset, shuffle=True, batch_size=batch_size)
        printloss = 0
        for batch_idx, (data, target) in enumerate(trainLoader):
            if self.usecuda:
                data = data.cuda()
                target = target.cuda()
            data = data.float()
            target = target.long()
            self.optimizer.zero_grad()
            out = self.model(data)
            loss = self.criterion(out, target)
            printloss += loss.item() * len(data)
            loss.backward()
            self.optimizer.step()
        print("Train Epoch:%d,Loss:%f\n" % (epoch, printloss/len(trainLoader.dataset)))

    def test(self, validdataset, batch_size):
        validLoader = DataLoader(dataset=validdataset, batch_size=batch_size, shuffle=False)
        self.model.eval()
        test_loss = 0
        correct = 0
        for data, target in validLoader:
            if self.usecuda:
                data = data.cuda()
                target = target.cuda()
            data = data.float()
            target = target.long()
            output = self.model(data)
            test_loss += self.criterion(output, target).data.item() * len(data)
            _, pred = torch.max(output, 1)
            num_correct = (pred == target).sum()
            correct += num_correct.item()

        test_loss /= len(validLoader.dataset)
        print('Dataset: Average loss: {:f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
            test_loss, correct, len(validLoader.dataset),
            100. * correct / len(validLoader.dataset)))
        return correct/len(validLoader.dataset)

    def predict(self, testDataset, batch_size=100):
        self.model.eval()
        test_loader = torch.utils.data.DataLoader(dataset=testDataset,
                                                  batch_size=batch_size, shuffle=False)
        pred = []
        for i, data in enumerate(test_loader):
            data = data[0].float()
            if torch.cuda.is_available():
                data = data.cuda()

            output = self.model(data)

            _, _pred = torch.max(output, 1)
            pred += _pred.tolist()
        data1 = {'ImageId': [i + 1 for i in range(len(pred))], 'Label': pred}
        df1 = pd.DataFrame(data1)
        df1.to_csv("./data/sample_submission.csv", index=None)
        return pred

 四种模型的训练都统一到这个类当中，其中损失函数使用的交叉熵，优化器用的Admm，尝试使用过RMSprop，发现没有Admm的效果好。

4、模型比较

 此次试验中，各种模型取得的最佳成绩：

MLP：0.9863 RNN：0.9917 LeNet5：0.9931 VGG：0.9962

 各模型的参数个数：

MLP：60790 RNN：57482 LeNet5：72734 VGG：393982

 可以发现MLP与RNN的最佳效果都没有CNN好，CNN在迭代次数比较少的情况下就能达到甚至超过MLP或RNN的效果。从模型参数数量可以发现，前三个模型参数个数差不多，不过LeNet5取得的成绩更佳。而VGG虽然效果不错，但模型参数达到了39万之多。

三、问题与思考

 1、随着迭代次数增加，训练集上的准确率会不断上升，而在测试集上的准确率将先上升后又下降，理论上应该在测试集达到最高准确率的时候停止。在本次实验中，我划分了训练集和验证集，但仍是固定迭代次数，迭代次数为40次。可以通过判断在验证集上的准确率，设定一个容忍度，例如若连续3次迭代验证集上的准确率都没有提高，就停止迭代。通过验证集调整的方法可以有效避免过拟合，但容忍度的设定也要有技巧，太小可能会过早停止，太大可能已经降低很多了才停止。固定迭代次数实现方便，而且在有了Dropout层的时候，似乎随迭代降低的现象不明显。其实还一种方式，还是固定迭代次数，但迭代过程中时刻保存当前训练得到的验证集准确率最大的模型的参数，作为最终训练出的模型。

 2、参数的初始化。在本次实验中，我没有采用初始化，但发现pytorch有默认的初始化，例如卷积层的默认初始化：

def reset_parameters(self):
    n = self.in_channels
    for k in self.kernel_size:
        n *= k
    stdv = 1. / math.sqrt(n)
    self.weight.data.uniform_(-stdv, stdv)
    if self.bias is not None:
        self.bias.data.uniform_(-stdv, stdv)

 采用的是零均值初始化，而实际训练中经常采用高斯分布初始化：

def weight_init(m):
    if isinstance(m, nn.Conv2d):
        n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
        m.weight.data.normal_(0, math.sqrt(2. / n))
    elif isinstance(m, nn.BatchNorm2d):
        m.weight.data.fill_(1)
        m.bias.data.zero_()

 3、过拟合问题，一般有这么几种方式：（1）早停（2）增强数据集（3）L1正则项（4）L2正则项（5）Dropout层。在这次实验中，我用上了L2正则项以及Dropout层，L2正则项只要在优化器中设置权重衰减系数，dropout层在模型建立的时候添加上。

 Dropout层效果很不错，通过随机修改隐层单元数来防止过拟合。

 4、CNN相比全连接神经网络的优点，CNN的特点在于局部连接和权值共享，在图像识别方面，若同样用全连接网络，将会面临巨大的参数量，而图像中的特征具有明显的局部性，例如图像的边缘可能是一些无用信息。用CNN正好可以减少参数量，同时仍能提取出重要的特征。因此CNN在图像方面有着很大的优势，但在其他领域优势就不那么突出。