树套树（树状数组套主席树）讲解

洛谷 P2617 Dynamic Rankings
This way

题意：

题解：

ZOJ只给32mb，我的空间复杂度是$O(nlo{g}^{2}n)$是真的过不去，但是也确实有能过去的树套树写法，我不是很理解。

由于已经养成了自己的代码风格，我在网上找不到和我的习惯类似的写法，他们也不讲清楚，没办法总是要有人站出来。献丑了！！！

在我写完之后，我意识到树套树和普通主席树有一个很大并且是本质的区别：他不会继承上一个点，而是继承了自己，更一般的说，他每个点都是一颗独立的主席树，他新增的值是继承(它-lowbit)位置的值，但是这两棵树又没有任何的联系，他们之间的关系更像是一个树状数组的前缀和，就像下图一样。但是由于每个点更新时增加的节点是$O(logn)$的，所以最终的空间复杂度是$O(nlo{g}^{2}n)$级别，


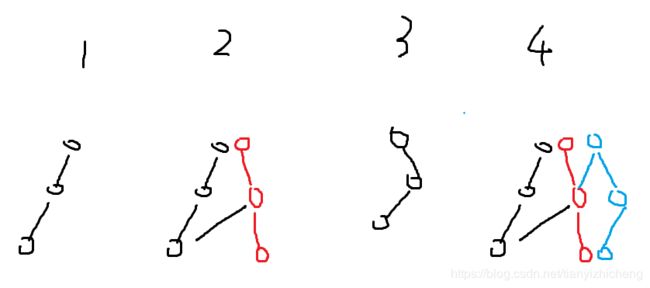
首先这道题目要用权值线段树方式去建树，那么我们必然需要先离散化所有的a和C修改中的y。
之后就是建树了，由于这道题需要单点修改，但是我们知道主席树如果修改了之前的某一个版本，那么之后继承这个版本的所有位置都需要修改。很明显我们不能每次$O(nlogn)$去修改，此时我们可以用树状数组来加速这个过程。
在我的代码中，Chairman结构体之内的函数是主席树的操作，在外部的update和query是树状数组的操作。
那么现在我们第i个主席树维护的就不是从上一个位置转移过来的值了，而是它在树状数组中所保存的那么多值，比如
1维护的是1
2维护的是1,2
3维护的是3
4维护的是1,2,3,4
然后查询3~4区间的话，就是区间4的值减去区间2的值。
在树状数组中，我们更新一个点必然是要将它后面的点更新，所以跳一下lowbit更新主席树。

void update(int l,int r,int root,int p,int v){
    for(int i=root;i<=n;i+=lowbit(i)){
        int now=++cmt.tot;
        cmt.update(l,r,now,cmt.rt[i],p,v);
        cmt.rt[i]=now;
    }
}

然后在查询的时候，我们查的就是组成r区间的所有的值的和-组成(l-1)区间的所有值的和。
比如说r是3的话，那么我们就要查rt[3]+rt[2]。
所以在query的时候，我们需要搞出两个数组，root表示组成右界的所有主席树，last表示组成左界-1的所有主席数。root[0]就表示有几个，last亦然。

int query(int l,int r,int k){
    root[0]=last[0]=0;
    for(int i=r;i;i-=lowbit(i))
        root[0]++,root[root[0]]=cmt.rt[i];
    for(int i=l-1;i;i-=lowbit(i))
        last[0]++,last[last[0]]=cmt.rt[i];
    return cmt.query(1,all,root,last,k);
}

在主席树内的query的时候，就和普通查k值的主席树差不多，但是需要查root和last数组的和。然后根据接下来去哪个子区间修改root和last数组的值。
很明显，区间查询的话，我们就需要新开一个root和last数组。

int query(int l,int r,int *root,int *last,int k){
    if(l==r)
        return l;
    int sum=0,mid=l+r>>1;
    for(int i=1;i<=root[0];i++)sum+=num[ls[root[i]]];
    for(int i=1;i<=last[0];i++)sum-=num[ls[last[i]]];
    if(sum>=k){
        for(int i=1;i<=root[0];i++)root[i]=ls[root[i]];
        for(int i=1;i<=last[0];i++)last[i]=ls[last[i]];
        return query(l,mid,root,last,k);
    }
    else{
        for(int i=1;i<=root[0];i++)root[i]=rs[root[i]];
        for(int i=1;i<=last[0];i++)last[i]=rs[last[i]];
        return query(mid+1,r,root,last,k-sum);
    }
}

最后，在询问时更新只需要将这个点的上一个值删掉，然后新增一个值就行了

			op[i].v=lower_bound(b+1,b+1+all,op[i].v)-b;
			update(1,all,op[i].x,a[op[i].x],-1);
			update(1,all,op[i].x,op[i].v,1);
			a[op[i].x]=op[i].v;

他们为什么要加上当前点的左儿子的值啊，为啥不是直接在树状数组里做？不是很懂，可能有别的处理吧。至少我洛谷的这道题过了，本来想着去BZOJ交一发看看情况的，但是他好像停运了…
不知道有没有别的办法能去BZOJ上交题，如果有哪位大佬知道的话欢迎留言或者私我

所以这个树套树暂时看来是没有问题的，如果哪里出错了可以留言或者私信，在之后我会改的。毕竟我也是第一次自己写树套树，参考了一些网上的思想，剩下的就靠自己对于树状数组和主席树的理解了。

如果哪里说的有问题，欢迎批评指正或许都是问题

※补充一点，由于每个主席树是独立的，所以在update的时候完全可以不用每一次都开空间，并且也不需要继承（为什么要继承自己呢），所以就有一种更省空间的写法：

void update(int l,int r,int &root,int p,int v){
        if(!root)root=++tot;
        num[root]+=v;
        if(l==r)return ;
        int mid=l+r>>1;
        if(mid>=p)
            update(l,mid,ls[root],p,v);
        else
            update(mid+1,r,rs[root],p,v);
    }

然后update的时候就可以这个样子：

void update(int l,int r,int root,int p,int v){
    for(int i=root;i<=n;i+=lowbit(i))
        cmt.update(l,r,cmt.rt[i],p,v);
}

时空复杂度都算尚可吧


最终的代码（未优化空间，想优化直接把上面的换上去就行了）：

#include
using namespace std;
const int N=2e5+5;
struct Chairman{
    int ls[N*200],rs[N*200],rt[N],num[N*200],tot;
    void init(){
        memset(rt,0,sizeof(rt));
        /*memset(ls,0,sizeof(ls));
        memset(rs,0,sizeof(rs));
        memset(num,0,sizeof(num));*/
        tot=0;
    }
    void update(int l,int r,int root,int last,int p,int v){
        ls[root]=ls[last];
        rs[root]=rs[last];
        num[root]=num[last]+v;
        if(l==r)return ;
        int mid=l+r>>1;
        if(mid>=p)
            update(l,mid,ls[root]=++tot,ls[last],p,v);
        else
            update(mid+1,r,rs[root]=++tot,rs[last],p,v);
    }
    int query(int l,int r,int *root,int *last,int k){
        if(l==r)
            return l;
        int sum=0,mid=l+r>>1;
        for(int i=1;i<=root[0];i++)sum+=num[ls[root[i]]];
        for(int i=1;i<=last[0];i++)sum-=num[ls[last[i]]];
        if(sum>=k){
            for(int i=1;i<=root[0];i++)root[i]=ls[root[i]];
            for(int i=1;i<=last[0];i++)last[i]=ls[last[i]];
            return query(l,mid,root,last,k);
        }
        else{
            for(int i=1;i<=root[0];i++)root[i]=rs[root[i]];
            for(int i=1;i<=last[0];i++)last[i]=rs[last[i]];
            return query(mid+1,r,root,last,k-sum);
        }
    }
}cmt;
int all,n,m;
int lowbit(int x){return x&(-x);}
void update(int l,int r,int root,int p,int v){
    for(int i=root;i<=n;i+=lowbit(i)){
        int now=++cmt.tot;
        cmt.update(l,r,now,cmt.rt[i],p,v);
        cmt.rt[i]=now;
    }
}
int root[50],last[50];
int query(int l,int r,int k){
    root[0]=last[0]=0;
    for(int i=r;i;i-=lowbit(i))
        root[0]++,root[root[0]]=cmt.rt[i];
    for(int i=l-1;i;i-=lowbit(i))
        last[0]++,last[last[0]]=cmt.rt[i];
    return cmt.query(1,all,root,last,k);
}
int a[N],b[N];
struct Operator{
    char op[2];
    int x,y,v;
}op[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]),b[i]=a[i];
    int cnt=n;
    for(int i=1;i<=m;i++){
        scanf("%s",op[i].op);
        if(op[i].op[0]=='Q')
            scanf("%d%d%d",&op[i].x,&op[i].y,&op[i].v);
        else
            scanf("%d%d",&op[i].x,&op[i].v),b[++cnt]=op[i].v;
    }
    sort(b+1,b+1+cnt);
    all=unique(b+1,b+1+cnt)-b-1;
    for(int i=1;i<=n;i++){
        a[i]=lower_bound(b+1,b+1+all,a[i])-b;
        update(1,all,i,a[i],1);
    }
    for(int i=1;i<=m;i++){
        if(op[i].op[0]=='Q')
            printf("%d\n",b[query(op[i].x,op[i].y,op[i].v)]);
        else{
            op[i].v=lower_bound(b+1,b+1+all,op[i].v)-b;
            update(1,all,op[i].x,a[op[i].x],-1);
            update(1,all,op[i].x,op[i].v,1);
            a[op[i].x]=op[i].v;
        }
    }
    return 0;
}