风机桨叶故障诊断(六) 利用自编码器进行特征学习
风机桨叶故障诊断(六) 利用自编码器进行特征学习
在之前的工作中,我已经初步构建了三层的BP神经网络,并已经从样本集的选取,模型的选择(隐含层神经元个数),和输出层神经元阈值选择这几个方面对桨叶的识别问题进行了优化。也得到了一些有用的结论:
1.我们的算法需要更多的数据,更多的数据对于提高算法的表现是有效的。
2.通过人为的控制神经网络输出层阈值可以降低误识率(以增大漏识率为代价)。
3.隐含层神经元个数选在25-100之间是最好的,更多的是无意义的反而会更糟,因为算法处于过拟合状态(换句话说还是缺少样本)。
通过以上分析,我们已经知道了哪些努力可以提升算法的表现。但是当前这个项目还处于在实验室测试算法的阶段,样本的问题目前是无法获取更多了,阈值我们也已通过实验选取了较为合理的数值。那么当前我们还能做些什么,来本质上的优化我们的算法,再之后再配合上更为好的样本集的选取,以达到理想的识别效果呢?
特征提取!!!
我思考了许久,发现我们漏掉了一个提升算法的重要途径,进行更好的特征提取。我之前完全默认在了对于图像识别的特征选择的一般方法中了,也就是选取图像的所有像素点的取值作为输入特征。虽然这是最普遍的做法,但是我们完全可以对原图像进行特征提取,用更具代表性的输入来训练我们的神经网络,下面就是思考如何进行特征提取了。
首先想到的便是边缘提取,用边缘像素信息代替原图像像素信息。不过我担心边缘提取后桨叶的信息只剩下两条线,很可能受到识别现场输电线的干扰。而且我们的算法目前已经处于过拟合状态,能够胜任较复杂的识别任务,只是还没提供足够的样本,所以边缘提取后损失大量的像素信息结果也许并不理想。(所有出现在我系列博文中的结论均是在得到实验的结果后给出的,但是这段我单独说明一下,只是我的猜测。相当于我在算法的优化上走到了一条多岔路口,有很多选择,我分析这条路可能走不长久,便选了另一条路,幸运的是恰巧得到了很好的结果,所以就没有再回过头来验证了我的这个想法对不对了)。
没有用边缘提取进行特征的提取,我想到的是一种自学习特征的方法。前些日子在看Andrew Ng的关于深度学习的教程的过程中,接触到了一个叫自编码器或自编码神经网络的算法。利用它可以很好的自我学习特征,我将它在深度学习中的一点点思想挪用到了我的算法中,取得了蛮不错的效果。下面来介绍下自编码神经网络:
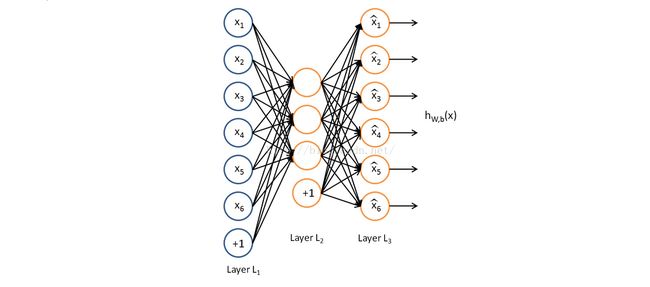
自编码神经网络是一种无监督学习算法,它使用了反向传播算法,并让目标值等于输入值,比如 ![]() 。也就是说,自编码神经网络与我们最熟悉的BP的区别仅仅在于它是个无监督学习算法,其实就是将输出设为与输入相同,传播算法与传递函数(本问题选sigmoid函数即可)均是一样的。下图是一个自编码神经网络的拓扑结构示例(图片来自Andrew Ng教程)。
。也就是说,自编码神经网络与我们最熟悉的BP的区别仅仅在于它是个无监督学习算法,其实就是将输出设为与输入相同,传播算法与传递函数(本问题选sigmoid函数即可)均是一样的。下图是一个自编码神经网络的拓扑结构示例(图片来自Andrew Ng教程)。
自编码神经网络尝试学习一个 ![]() 的函数。换句话说,它尝试逼近一个恒等函数,从而使得输出
的函数。换句话说,它尝试逼近一个恒等函数,从而使得输出 ![]() 接近于输入
接近于输入 ![]() 。恒等函数虽然看上去不太有学习的意义,但是当我们为自编码神经网络加入某些限制,比如限定隐藏神经元的数量,我们就可以从输入数据中发现一些有趣的结构。举例来说,假设某个自编码神经网络的输入
。恒等函数虽然看上去不太有学习的意义,但是当我们为自编码神经网络加入某些限制,比如限定隐藏神经元的数量,我们就可以从输入数据中发现一些有趣的结构。举例来说,假设某个自编码神经网络的输入 ![]() 是一张
是一张 ![]() 图像(共100个像素)的像素灰度值,于是
图像(共100个像素)的像素灰度值,于是 ![]() ,其隐藏层
,其隐藏层 ![]() 中有50个隐藏神经元。它必须从50维的隐藏神经元激活度向量
中有50个隐藏神经元。它必须从50维的隐藏神经元激活度向量 ![]() 中重构出100维的像素灰度值输入
中重构出100维的像素灰度值输入 ![]() 。如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性。
。如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性。
既然自编码器可以从一些相关的输入中发现其隐含着的特定结构并提取出来,我就想到用自编码神经网络为我们进行特征提取,对图像像素值输入进行提取。注意我们由自编码器的特点可以看出,让它从具有特定结构的输入中提取才是有意义的。所以我的做法是,把正样本集和负样本集分别放入自编码器进行训练(注意是分别训练)。
然后我们对于某一个样本集(比如正样本集)训练完的结果,利用训练得到的模型参数 ![]() (分别代表隐含层到输入层连接权重矩阵,偏置神经元连接权重向量;输出层到隐含层连接权重矩阵,偏置神经元连接权重向量),给定任意的输入数据
(分别代表隐含层到输入层连接权重矩阵,偏置神经元连接权重向量;输出层到隐含层连接权重矩阵,偏置神经元连接权重向量),给定任意的输入数据 ![]() ,可以计算隐藏单元的激活量(activations)
,可以计算隐藏单元的激活量(activations) ![]() 。如前所述,相比原始输入
。如前所述,相比原始输入 ![]() 来说,
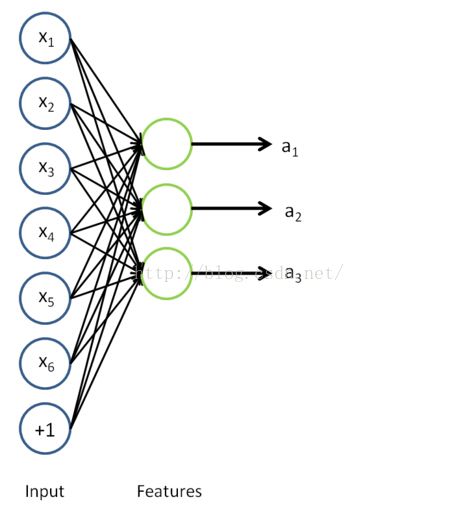
来说,![]() 可能是一个更好的特征描述。下图的神经网络描述了特征(激活量
可能是一个更好的特征描述。下图的神经网络描述了特征(激活量 ![]() )的计算。
)的计算。
这实际上就是之前得到的稀疏自编码器,在这里去掉了最后一层。对于负样本集我们可以同样的训练完后去掉最后一层。我们是分着进行训练的,这样做相当于分别为正样本和负样本找到了更好的特征描述。然后我们可以将得到的结果进行整合,也就是将得到的权重矩阵合并到一起,这样没有改变任何东西,只是相当于两个神经网络整合成了一个,同时拥有了对正负样本更好的特征表达。按照我的理解,当我们输入一个正样本时,用来训练正样本得到的那些隐含层神经元会表现的比较活跃,因为它们看到了熟悉的结构熟悉的小伙伴!~反过来负样本是同理的,我认为这是自编码器能够发挥很好效果的所在。在实践中,我正负样本集上分别各训练了含50个神经元的自编码神经网络,然后将其合在了一起。这样,每当我得到了一幅图片,我可以将其变换为一个100维的输入向量,并且这个向量对于计算机来说是更好的特征表达。对于所有的样本都做相同的处理,得到了新的特征提取后的样本集。最后一步就是将新的样本集输入我们原来的算法进行训练,我们来期待一下效果!
首先算法随机展示了100个样本,显然人眼已经完全看不出图像原来的内容和轮廓,但是我们可以明显的将样本分为两类,这说明了我们的自编码器很好的提取了计算机看起来更好的特征,如下图所示:
然后开始训练,最大迭代次数设置为1000次。最后的输出结果如下:
-----------------------------------------------------------------------------
Iteration 998 | Cost: 7.793451e-01
Iteration 999 | Cost: 7.793416e-01
Iteration 1000 | Cost: 7.793044e-01
Program paused. Press enter to continue.
Visualizing Neural Network...
Program paused. Press enter to continue.
Training Set Accuracy: 86.571429
Test Set Accuracy: 80.402010
发生假阳性错误的概率(把一个负样本估计成正样本的概率): 0.000000
真阳性的概率(把一个正样本估计成正样本的概率): 38.095238
-----------------------------------------------------------------------------
对比之前没有进行特征提取的结果,算法在训练样本集上的准确率有所下降(之前在90%偏上浮动),在测试样本集上准确率明显上升(之前的70%-75%)。这说明我们的算法对于输入特性的更好的理解也一定程度解决了算法过拟合的问题,这确实是意外收获!此外,我们之前说过,对于我们的具体问题,我们最关心的是发生假阳性错误的概率能否很低,而对正样本的识别率可以放宽。优于神经网络每次输出结果都会有差异,为了结果的可靠性,我都是采用多次训练并记录结果。我找出了之前记录的算法的表现记录,列出如下表格进行对比:
| 普通BP神经网络训练结果 | 图像进行特征提取后的BP神经网络训练结果 | ||
| 假阳性错误的概率 | 真阳性概率 | 假阳性错误的概率 | 真阳性概率 |
| 3.517588 | 14.070352 | 0 | 38.095238 |
| 4.020101 | 19.59799 | 2.068966 | 38.888889 |
| 4.522613 | 21.60804 | 2.919708 | 48.387097 |
| 5.025126 | 14.070352 | 1.41844 | 39.655172 |
| 4.522613 | 19.095477 | 0.675676 | 41.176471 |
由结果可以看出,由于算法对于输入有了更好的认识,假阳性错误的概率进一步的降低,并且已经到了可以接受的范围内了。同时正样本的识别率也明显的上升了,这也就给了我们通过修改输出层阈值来减小假阳性错误的概率更大的空间(尽管已经很满意了),因为正样本的识别率已经远超我们的预期要求了。
今天就到这里了,改进后的算法表现真的大超我的预期,真是太兴奋了!今天进展很大,收获很大,加油↖(^ω^)↗