Java常用的八种排序算法与代码实现
- 1、直接插入排序
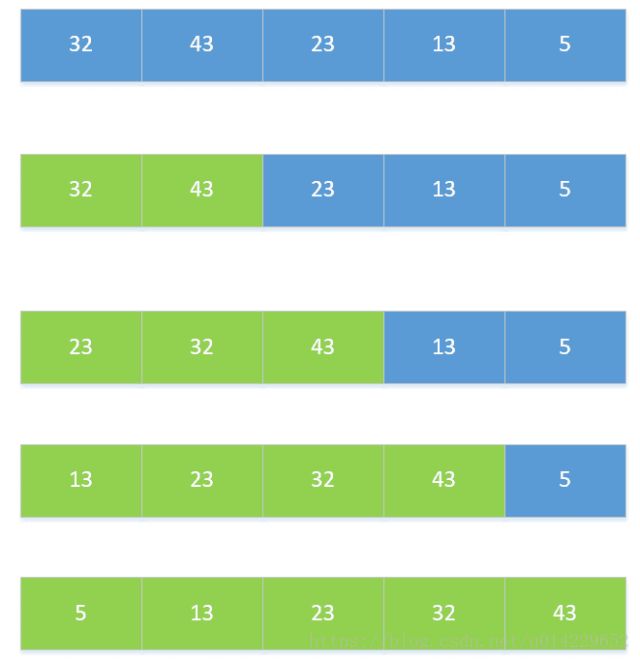
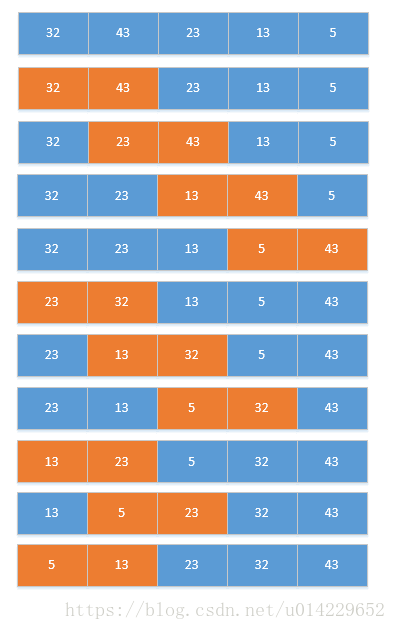
我们经常会到这样一类排序问题: 把新的数据插入到已经排好的数据列中。将第一个数和第二个数排序,然后构成一个有序序列将第三个数插入进去,构成一个新的有序序列。对第四个数、第五个数……直到最后一个数,重复第二步。如题所示:
直接插入排序(Straight Insertion Sorting)的基本思想:在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
代码实现:
首先设定插入次数,即循环次数,for(int i=1;i
public void insertSort(int [] a){
int len=a.length;//单独把数组长度拿出来,提高效率
int insertNum;//要插入的数
for(int i=1;i//因为第一次不用,所以从1开始
insertNum=a[i];
int j=i-1;//序列元素个数
while(j>=0&&a[j]>insertNum){//从后往前循环,将大于insertNum的数向后移动
a[j+1]=a[j];//元素向后移动
j--;
}
a[j+1]=insertNum;//找到位置,插入当前元素
}
} - 2、希尔排序
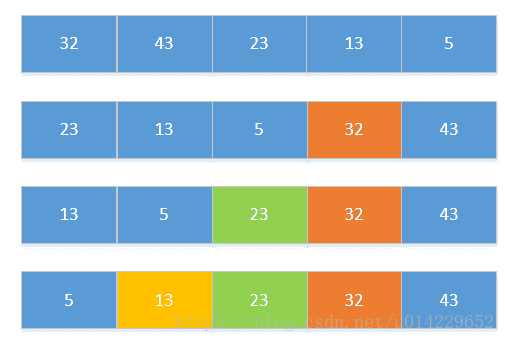
针对直接插入排序的下效率问题,有人对次进行了改进与升级,这就是现在的希尔排序。希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率
但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位
如图所示:
对于直接插入排序问题,数据量巨大时。
将数的个数设为n,取奇数k=n/2,将下标差值为k的数分为一组,构成有序序列。
再取k=k/2 ,将下标差值为k的书分为一组,构成有序序列。
重复第二步,直到k=1执行简单插入排序。
代码实现:
首先确定分的组数。
然后对组中元素进行插入排序。
然后将length/2,重复1,2步,直到length=0为止。
public void sheelSort(int [] a){
int len=a.length;//单独把数组长度拿出来,提高效率
while(len!=0){
len=len/2;
for(int i=0;i//分组
for(int j=i+len;j//元素从第二个开始
int k=j-len;//k为有序序列最后一位的位数
int temp=a[j];//要插入的元素
/*for(;k>=0&&temp
while(k>=0&&temp//从后往前遍历
a[k+len]=a[k];
k-=len;//向后移动len位
}
a[k+len]=temp;
}
}
}
}
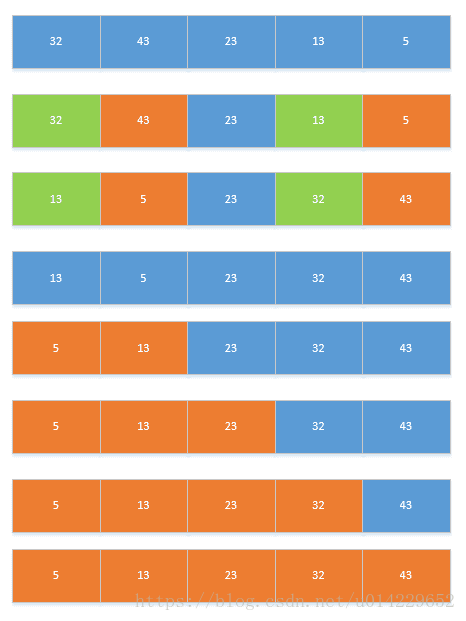
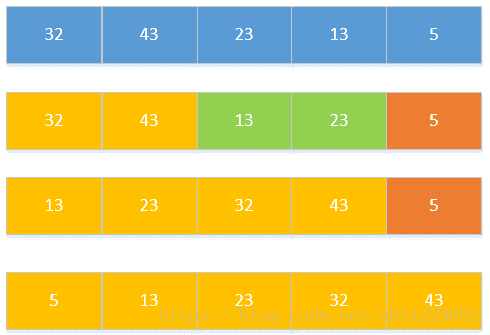
- 3、简单选择排序
常用于取序列中最大最小的几个数时。
(如果每次比较都交换,那么就是交换排序;如果每次比较完一个循环再交换,就是简单选择排序。)
遍历整个序列,将最小的数放在最前面。
遍历剩下的序列,将最小的数放在最前面。
重复第二步,直到只剩下一个数。
代码实现:
首先确定循环次数,并且记住当前数字和当前位置。
将当前位置后面所有的数与当前数字进行对比,小数赋值给key,并记住小数的位置。
比对完成后,将最小的值与第一个数的值交换。
重复2、3步。
public void selectSort(int[]a){
int len=a.length;
for(int i=0;i//循环次数
int value=a[i];
int position=i;
for(int j=i+1;j//找到最小的值和位置
if(a[j]//进行交换
a[i]=value;
}
}
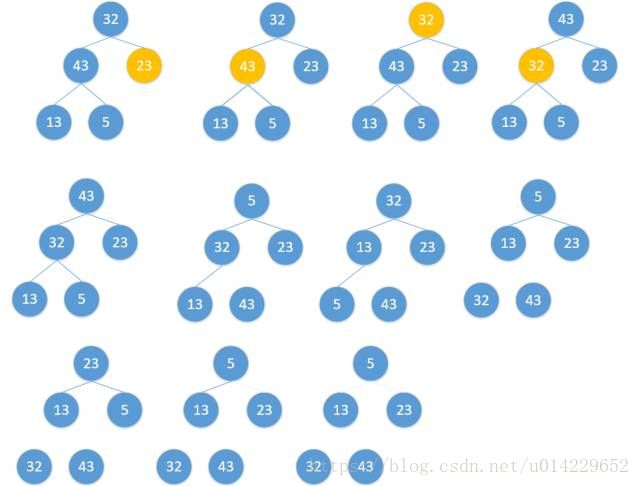
代码如下:
public void heapSort(int[] a){
int len=a.length;
//循环建堆
for(int i=0;i1;i++){
//建堆
buildMaxHeap(a,len-1-i);
//交换堆顶和最后一个元素
swap(a,0,len-1-i);
}
}
//交换方法
private void swap(int[] data, int i, int j) {
int tmp=data[i];
data[i]=data[j];
data[j]=tmp;
}
//对data数组从0到lastIndex建大顶堆
private void buildMaxHeap(int[] data, int lastIndex) {
//从lastIndex处节点(最后一个节点)的父节点开始
for(int i=(lastIndex-1)/2;i>=0;i--){
//k保存正在判断的节点
int k=i;
//如果当前k节点的子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
if(biggerIndex//若果右子节点的值较大
if(data[biggerIndex]1]){
//biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
//如果k节点的值小于其较大的子节点的值
if(data[k]//交换他们
swap(data,k,biggerIndex);
//将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值
k=biggerIndex;
}else{
break;
}
}
}
}
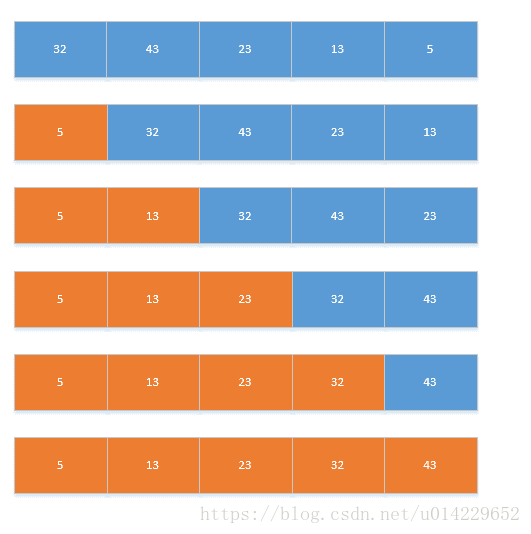
- 5、冒泡排序
很简单,用到的很少,据了解,面试的时候问的比较多!
将序列中所有元素两两比较,将最大的放在最后面。
将剩余序列中所有元素两两比较,将最大的放在最后面。
重复第二步,直到只剩下一个数。
代码实现:
设置循环次数。
设置开始比较的位数,和结束的位数。
两两比较,将最小的放到前面去。
重复2、3步,直到循环次数完毕。
public void bubbleSort(int []a){
int len=a.length;
for(int i=0;ifor(int j=0;j1;j++){//注意第二重循环的条件
if(a[j]>a[j+1]){
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
} 6.快速排序
要求时间最快时。
选择第一个数为p,小于p的数放在左边,大于p的数放在右边。
递归的将p左边和右边的数都按照第一步进行,直到不能递归。
public void quickSort(int[]a,int start,int end){
if(startint baseNum=a[start];//选基准值
int midNum;//记录中间值
int i=start;
int j=end;
do{
while((a[i]while((a[j]>baseNum)&&j>start){
j--;
}
if(i<=j){
midNum=a[i];
a[i]=a[j];
a[j]=midNum;
i++;
j--;
}
}while(i<=j);
if(startif(end>i){
quickSort(a,i,end);
}
}
}
- 7、归并排序
速度仅次于快速排序,内存少的时候使用,可以进行并行计算的时候使用。
选择相邻两个数组成一个有序序列。
选择相邻的两个有序序列组成一个有序序列。
重复第二步,直到全部组成一个有序序列。
public void mergeSort(int[] a, int left, int right) {
int t = 1;// 每组元素个数
int size = right - left + 1;
while (t < size) {
int s = t;// 本次循环每组元素个数
t = 2 * s;
int i = left;
while (i + (t - 1) < size) {
merge(a, i, i + (s - 1), i + (t - 1));
i += t;
}
if (i + (s - 1) < right)
merge(a, i, i + (s - 1), right);
}
}
private static void merge(int[] data, int p, int q, int r) {
int[] B = new int[data.length];
int s = p;
int t = q + 1;
int k = p;
while (s <= q && t <= r) {
if (data[s] <= data[t]) {
B[k] = data[s];
s++;
} else {
B[k] = data[t];
t++;
}
k++;
}
if (s == q + 1)
B[k++] = data[t++];
else
B[k++] = data[s++];
for (int i = p; i <= r; i++)
data[i] = B[i];
}
8、基数排序
用于大量数,很长的数进行排序时。
将所有的数的个位数取出,按照个位数进行排序,构成一个序列。
将新构成的所有的数的十位数取出,按照十位数进行排序,构成一个序列。代码实现:
public void baseSort(int[] a) {
//首先确定排序的趟数;
int max = a[0];
for (int i = 1; i < a.length; i++) {
if (a[i] > max) {
max = a[i];
}
}
int time = 0;
//判断位数;
while (max > 0) {
max /= 10;
time++;
}
//建立10个队列;
List> queue = new ArrayList>();
for (int i = 0; i < 10; i++) {
ArrayList queue1 = new ArrayList();
queue.add(queue1);
}
//进行time次分配和收集;
for (int i = 0; i < time; i++) {
//分配数组元素;
for (int j = 0; j < a.length; j++) {
//得到数字的第time+1位数;
int x = a[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
ArrayList queue2 = queue.get(x);
queue2.add(a[j]);
queue.set(x, queue2);
}
int count = 0;//元素计数器;
//收集队列元素;
for (int k = 0; k < 10; k++) {
while (queue.get(k).size() > 0) {
ArrayList queue3 = queue.get(k);
a[count] = queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}
新建测试类进行测试
public class TestSort {
public static void main(String[] args) {
int []a=new int[10];
for(int i=1;i//a[i]=(int)(new Random().nextInt(100));
a[i]=(int)(Math.random()*100);
}
System.out.println("排序前的数组为:"+Arrays.toString(a));
Sort s=new Sort();
//排序方法测试
//s.insertSort(a);
//s.sheelSort(a);
//s.selectSort(a);
//s.heapSort(a);
//s.bubbleSort(a);
//s.quickSort(a, 1, 9);
//s.mergeSort(a, 3, 7);
s.baseSort(a);
System.out.println("排序后的数组为:"+Arrays.toString(a));
}
}
部分结果如下:
如果要进行比较可已加入时间,输出排序时间,从而比较各个排序算法的优缺点,这里不再做介绍。
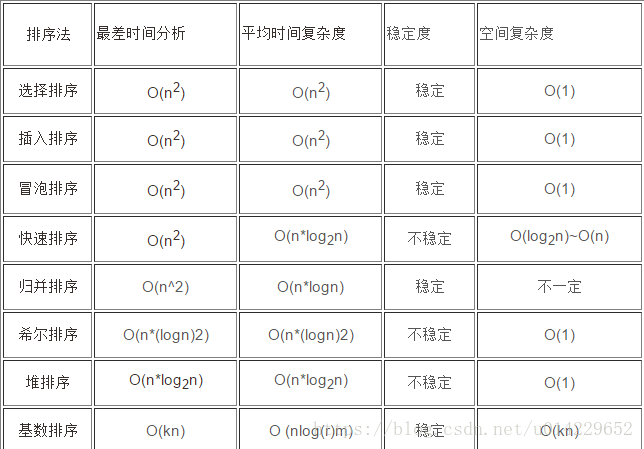
8、总结:
一、稳定性:稳定:冒泡排序、插入排序、归并排序和基数排序
不稳定:选择排序、快速排序、希尔排序、堆排序
二、平均时间复杂度
O(n^2):直接插入排序,简单选择排序,冒泡排序。
在数据规模较小时(9W内),直接插入排序,简单选择排序差不多。当数据较大时,冒泡排序算法的时间代价最高。性能为O(n^2)的算法基本上是相邻元素进行比较,基本上都是稳定的。
O(nlogn):快速排序,归并排序,希尔排序,堆排序。
其中,快排是最好的, 其次是归并和希尔,堆排序在数据量很大时效果明显。
三、排序算法的选择
1.数据规模较小
(1)待排序列基本序的情况下,可以选择直接插入排序;
(2)对稳定性不作要求宜用简单选择排序,对稳定性有要求宜用插入或冒泡
2.数据规模不是很大
(1)完全可以用内存空间,序列杂乱无序,对稳定性没有要求,快速排序,此时要付出log(N)的额外空间。
(2)序列本身可能有序,对稳定性有要求,空间允许下,宜用归并排序
3.数据规模很大
(1)对稳定性有求,则可考虑归并排序。
(2)对稳定性没要求,宜用堆排序
4.序列初始基本有序(正序),宜用直接插入,冒泡
各算法复杂度如下: