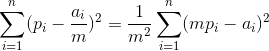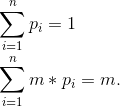【2019牛客暑期ACM集训多校第一场】

1.A题。RMQ+二分。比较easy，不再多说。

#include
using namespace std;


const int maxn = 1e5 + 5, lgmaxn = 20;
int n, a[maxn], b[maxn];
static int lg[maxn];

struct RMQ {
	int mx[maxn][lgmaxn];

	RMQ() {//构造函数
		if (lg[2] != 1) {
			for (int i = 2; i < maxn; i++) { //因为lg(1)=0
				lg[i] = (i & -i) == i ? lg[i - 1] + 1 : lg[i - 1];
			}
		}
	}

	void build(int n, int* a) {
		for (int i = 0; i <= n; i++)mx[i][0] = a[i];
		for (int j = 1; j <= lg[n + 1]; j++)
			for (int i = 0; i + (1 << j) - 1 <= n; i++)
				mx[i][j] = min(mx[i][j - 1], mx[i + (1 << (j - 1))][j - 1]);
	}

	int query(int l, int r) {
		int k = lg[r - l + 1];
		return min(mx[l][k], mx[r - (1 << k) + 1][k]);
	}

	int queryminidx(int d)
	{
		if (query(1, d) == query(d, d))return d;
		int l = 1,r = d + 1;
		while (l + 1 < r)
		{
			int mid = (l + r) >> 1;
			if (query(mid, d) < query(d, d))l = mid;
			else r = mid;
		}
		return l;
	}

}r1, r2;


int main()
{
	while (~scanf("%d", &n))
	{
		for (int i = 1; i <= n; i++) scanf("%d", a + i);
		for (int i = 1; i <= n; i++) scanf("%d", b + i);
		r1.build(n, a);
		r2.build(n, b);
		int ans = 0;


		for (int i = 1; i <= n; i++) {
			if (r1.queryminidx(i) == r2.queryminidx(i)) ans = i;
			else break;
		}
		printf("%d\n", ans);
	}
}

2.B题。先搞一下两项，然后每次从后边拿出来一项乘进来，然后继续裂项，可以模拟或者dfs或者直接推完。

#include 
 
using namespace std;
const int mod = 1e9 + 7;
 
int qpow(int a, int b) {
    int ret = 1;
    while (b) {
        if(b&1)ret = 1ll * ret*a%mod;
        a = 1ll * a*a%mod;
        b >>= 1;
    }
    return ret;
}
 
int rev(int x) {
    return qpow(x, mod - 2);
}
 
struct node {
    int k, a;
};
 
void merge(node a, node b, node&ret1, node&ret2) {
    int mul = 1ll*a.k*b.k%mod;
    int r = rev((1ll * b.a*b.a - 1ll * a.a*a.a%mod + mod) % mod);
    ret1.a = a.a;
    ret1.k = 1ll * mul * r%mod;
    ret2.a = b.a;
    ret2.k = mod - 1ll * mul * r%mod;
}
 
int main() {
    //cout << rev(1120) << endl;
    //cout << rev(120) << endl;
    int n;
    while (cin >> n) {
        vector front, back;
        for (int i = 0; i < n; i++) {
            int a; cin >> a;
            back.push_back(node{ 1,a });
        }
        front.push_back(back.back());
        back.pop_back();
        while (!back.empty()) {
            node sum = back.back();
            sum.k = 0;
 
            for (int i = 0; i < front.size(); i++) {
                node a, b;
                merge(front[i],back.back(),a,b);
                front[i] = a;
                sum.k = (sum.k + b.k) % mod;
            }
            front.push_back(sum);
            back.pop_back();
        }
        int ans = 0;
        for (int i = 0; i < front.size(); i++) {
            // cout << front[i].k << " " << front[i].a << endl;
            ans = (ans + 1ll*front[i].k*rev(2*front[i].a)) % mod;
        }
        cout << ans << endl;
    }
}

3.C题。给定一个n维空间的平面（加了限制），找一个点到这个平面的距离最短。这个题目，其实很简单，但是被搞了，完全没啥必要用拉格朗日乘子。贪心就可以过了。重点说一下这个题目：

                                                         

我们首先把分母拿出来，然后分析这个式子，由于：

                                                     

那么就相当于我们现在有n个数据他们的总和为m，然后用他们来消减ai,使得答案最小，那么我们该怎么分配每个ai得到的值呢？

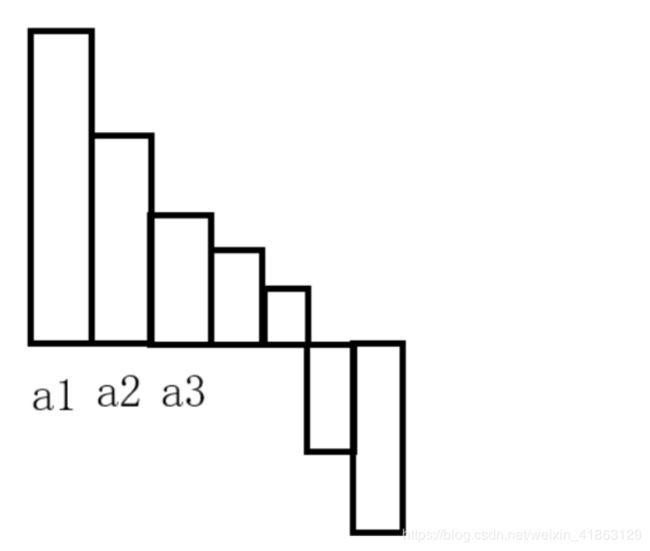
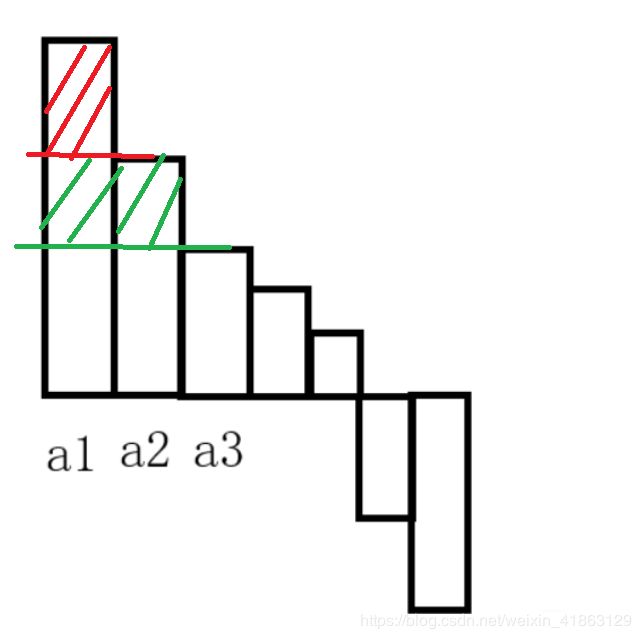
显然，我们可以贪心，我们一定是先把最大的给消减掉，因为它如果很大就会对答案造成很大的贡献，或者我们形象的来说明。

                                                     

 

                         

 

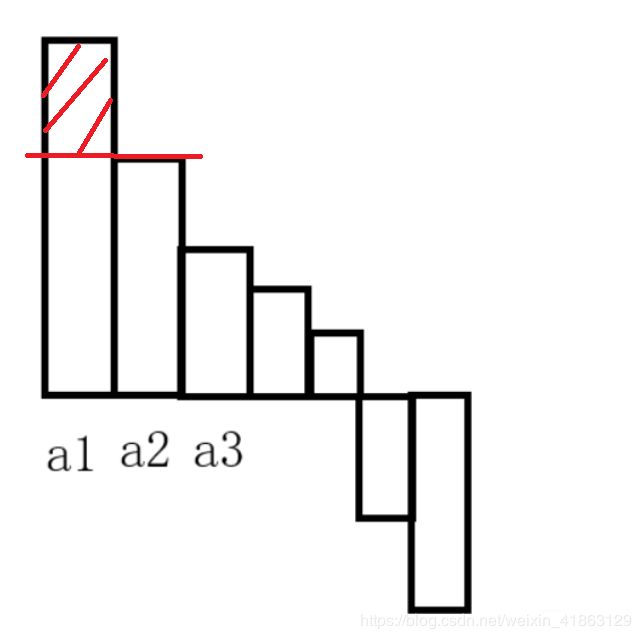
我们把a排序之后，会出现这样的情况。那么我们先把a1给推平，让它和a2一样高

然后如果m还有剩余，就继续推：

直到m被用完，那么会把前k个推成a[k]-r/k.然后，后面的n-k个就没有任何变化，为了好算，同时扩大k 倍，然后就两边各自算一下即可。

#include
using namespace std;
#define ll long long
const int maxn = 1e4 + 10;
ll __gcd(ll a, ll b)
{
	return b == 0 ? a : __gcd(b, a % b);
}
ll a[maxn];
int n;
ll m;
int main()
{
	while (~scanf("%lld%lld", &n, &m))
	{
		for (int i = 1; i <= n; i++)
		{
			scanf("%lld", &a[i]);
		}
		sort(a + 1, a + n + 1, greater());
		ll r = m;
		ll pos = 1;
		while (pos < n)
		{
			if (r < (a[pos] - a[pos + 1]) * pos)break;
			r -= (a[pos] - a[pos + 1]) * pos;
			pos++;
		}
		//结果最后一定是被处理为a[pos]-r/pos
		ll ans = (a[pos] * pos - r) * (a[pos] * pos - r) * pos;
		ll fenmu = m * m * pos * pos;
		for (int i = pos + 1; i <= n; i++)
		{
			ans += a[i] * a[i] * pos * pos;
		}
		ll gcd = __gcd(ans, fenmu);
		ans = ans / gcd;
		fenmu = fenmu/ gcd;
		if (fenmu == 1)
		{
			printf("%lld\n", ans);
		}
		else
		{
			printf("%lld/%lld\n", ans, fenmu);
		}
	}

	return 0;
}

4.E题。DP，但是这个思路有点奇怪，不是很懂，队友AC的。

#include
using namespace std;
int n,m,f[4010][2010],mod=1e9+7;
int main()
{
    while(~scanf("%d %d",&n,&m))
    {
        f[0][0]=1;
        for(int i=1; i<=(n+m)*2; i++)
            for(int j=0; j<=m+n; j++)
            {
                if(i-j*2>m||2*j-i>n)
                    f[i][j]=0;
                else
                    f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;
            }
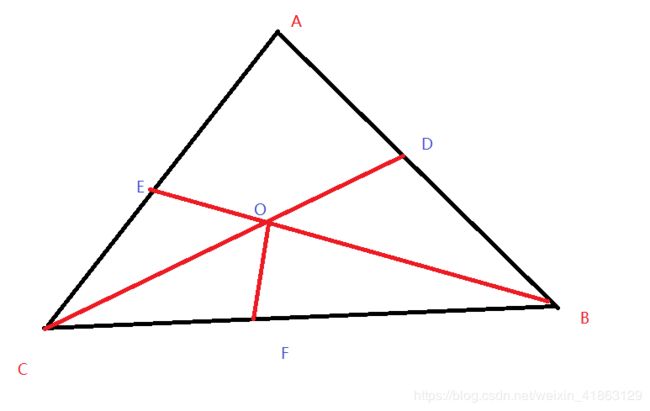
        cout<

5.F题。首先找到可以把三角形面积三等分点是中心。

重心O可以把三角形分割成三个四边形，AEDO，CEOF，ODBF。现在把三角形立起来，考虑AEDO，那么再这个区域内的所有点，都会选择BC作为边（可以证明），计算这个区域内的期望，就相当于计算每个点的势能之和。最后搞一搞就是三角形面积的11倍。

6.H题，线性基的使用。转化一下：等价于求解：.count(a_i)表示包含ai并且异或和等于0的所有集合的个数。然后把线性基和非线性基分别计算一下就是答案。对于非线性基每个元素的贡献是相同的，比如有n个元素，线性基含有k个，非线性基含有n-k个。那么每个元素的贡献就是：pow(2,n-k-1).为什么？因为剩下的n-k-1个元素，每个元素都是两种状态，选或者不选，这样会产生一个集合，然后这个集合在线性基内部会有唯一一个集合与之对应，加上这个集合让它异或为0，至于线性基集合内部，直接暴力算即可。

#include
using namespace std;
 
#define inf  1000000000
#define mod 1000000007
#define maxn 100005
 
#define pb push_back
#define mp make_pair
#define F first
#define S second
#define pii pair
 
#define debug cout<<"hi"<=mod) a-=mod;}
inline void decmod(int &a,int b){a-=b;if(a<0)a+=mod;}
inline void addmod(ll &a,ll b){a+=b;if(a>=mod) a-=mod;}
inline void decmod(ll &a,ll b){a-=b;if(a<0)a+=mod;}
 
/********** show time **********/
 
struct LB
{
    static const ll maxbit=63;
    ll b[maxbit],tot;
 
    void ini()
    {
        tot=0;
        memset(b,0,sizeof(b));
    }
    bool ins(ll x)
    {
        for(ll i=maxbit-1; i>=0; i--)
            if(x&(1ll<0;
    }
 
} l1,l2,l3;
 
ll qp(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1)
            res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}
 
ll n,x;
int main()
{
    while(~scanf("%lld",&n))
    {
        vectora,b,c;
        ll ans=0;
        l1.ini();
        for(ll i=1; i<=n; i++)
        {
            scanf("%lld",&x);
            if(l1.ins(x))
                a.pb(x);
            else
                b.pb(x);
        }
        ll sz=a.size();
        ans+=(n-sz)*qp(2,n-sz-1)%mod;
 
 
        l3.ini();
        ll cnt=0;
        for(ll i=0;i

7.I题，线段树维护DP，队友搞得，还没补。

#include
 
using namespace std;
typedef long long ll;
 
#define ml ((l+r)>>1)
#define mr (ml+1)
const ll maxn=1e5+15;
ll add[maxn*2],mx[maxn*2],ls[maxn*2],rs[maxn*2],tot;
 
void push_son(ll&son,ll l,ll r,ll addrt){// 这个函数要注意重写
    if(son==0) {
        son=++tot;
        add[son]=0;
        mx[son]=0;
        ls[son]=0;
        rs[son]=0;
    }
    if(addrt!=0){
        mx[son]+=addrt;
        add[son]+=addrt;
    }
}
 
void push_down(ll rt,ll l,ll r){
    push_son(ls[rt],l,ml,add[rt]);// 这行要注意重写
    push_son(rs[rt],mr,r,add[rt]);// 这行要注意重写
    add[rt]=0;// 这行要注意重写
}
 
void push_up(ll rt,ll l,ll r){
    mx[rt]=max(mx[ls[rt]],mx[rs[rt]]);// 这行要注意重写
}
 
void build(ll&rt,ll l,ll r){
    rt=tot=0;
    push_son(rt,l,r,0);// 这行要注意重写
}
 
void update(ll rt,ll l,ll r,ll ql,ll qr,ll d){//
    if(ql<=l&&r<=qr){// 这行要注意重写
        push_son(rt,l,r,d);//add
        return;
    }
    push_down(rt,l,r);
    if(ml>=ql) update(ls[rt],l,ml,ql,qr,d);
    if(mr<=qr) update(rs[rt],mr,r,ql,qr,d);
    push_up(rt,l,r);
}
 
ll query(ll rt,ll l,ll r,ll ql,ll qr){
    if(ql<=l&&r<=qr) return mx[rt];// 这行要注意重写
    push_down(rt,l,r);
    ll ret=0;// 这行要注意重写
    if(ml>=ql) ret=max(ret,query(ls[rt],l,ml,ql,qr));// 这行要注意重写
    if(mr<=qr) ret=max(ret,query(rs[rt],mr,r,ql,qr));// 这行要注意重写
    return ret;
}
 
struct node{ll x,y,a,b;};
 
int main() {
    ios::sync_with_stdio(false);
    ll n;
    while(cin>>n){
        n+=2;
        vector p(n);
        vector disc(n);
        for(ll i=0;i>p[i].x>>p[i].y>>p[i].a>>p[i].b;
        p[n-2]=node{0ll,ll(-1e18),0ll,0ll};
        p[n-1]=node{0ll,ll(1e18) ,0ll,0ll};
        for(ll i=0;i idx;
        for(ll i=0;ians;
                for(ll  j:idx) {
                    ll oldval=query(rt,1,siz,p[j].y,p[j].y);
                    ll newval=query(rt,1,siz,1,p[j].y);
                    ans.push(newval-oldval);
                }
                for(ll  j:idx){
                    update(rt,1,siz,p[j].y,p[j].y,ans.front()); ans.pop();
                    if(p[j].y-1>=1)update(rt,1,siz,1,p[j].y-1,p[j].a);
                    if(siz>=p[j].y)update(rt,1,siz,p[j].y,siz,p[j].b);
                }
                idx.clear();
            }
        }
        cout<