Python时间序列分析(ARIMA模型回归,决策树二分类)
文章目录
- 1. 时间序列
- 1.1 date_range
- 1.2 truncate过滤
- 1.3 Timestamp,Period,Timedelta
- 1.4 时间转换
- 1.5 period_range
- 1.6 指定索引
- 1.7 时间戳Timestamp 和时间周期period 转换
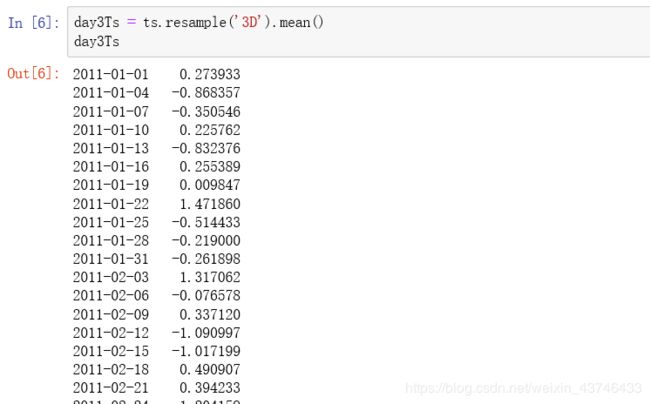
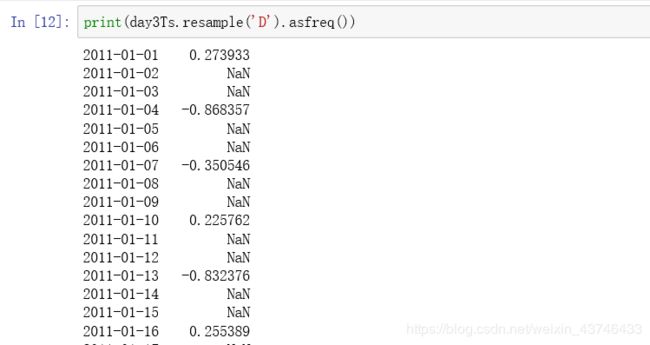
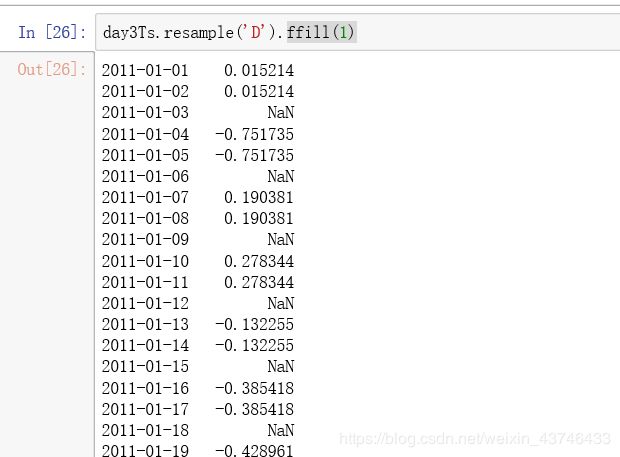
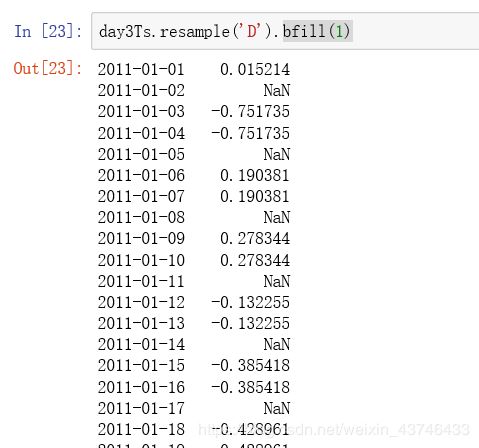
- 1.8 时间序列插值
- 2.股价预测(回归)
- 2.1 查看数据
- 2.2 取Close列每周的平均值
- 2.3 Close列每周的平均值绘制折线图
- 2.4 一阶分差,提高平稳性
- 2.5 ACF,PACF
- 2.6 ARIMA模型
- 2.7 总结
- 3. 对tsfresh库中机器人执行失败数据集分类(二分类)
- 3.1 查看数据
- 3.2 绘制不同传感器的数据随时间变化
- 3.3 时间序列特征提取
- 3.4 用决策树模型训练,预测,评估
1. 时间序列
1.1 date_range
- 时间戳(timestamp)
- 固定周期(period)
- 时间间隔(interval)
可以指定开始时间与周期
- H:小时
- D:天
- M:月
rng = pd.date_range('2016-07-01', periods = 10, freq = '3D')
rng
import datetime as dt
time=pd.Series(np.random.randn(20),index=pd.date_range(dt.datetime(2016,1,1),periods=20))
print(time)
1.2 truncate过滤
time.truncate(before='2016-1-10')
time.truncate(after='2016-1-10')
print(time['2016-01-15':'2016-01-20'])
data=pd.date_range('2010-01-01','2011-01-01',freq='M')
print(data)
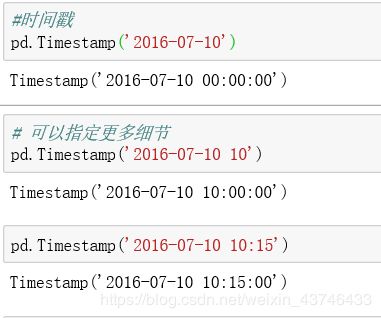
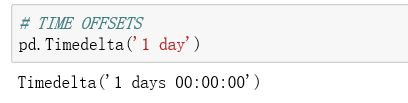
1.3 Timestamp,Period,Timedelta
1.4 时间转换
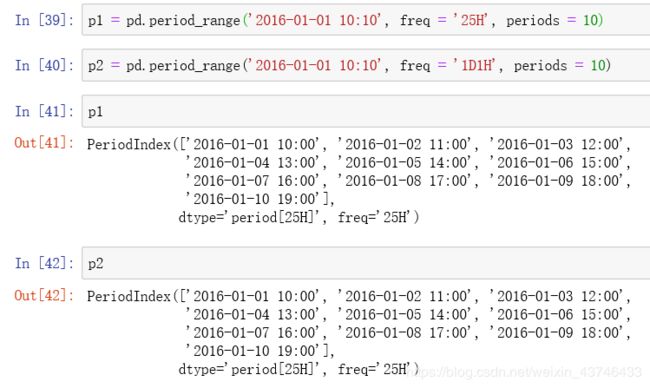
1.5 period_range
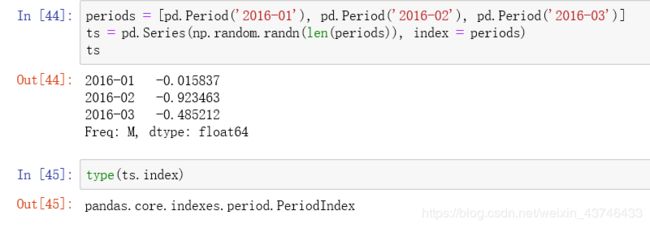
1.6 指定索引
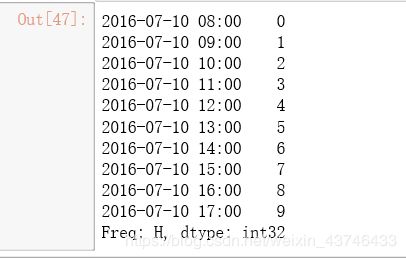
1.7 时间戳Timestamp 和时间周期period 转换
ts = pd.Series(range(10), pd.date_range('07-10-16 8:00', periods = 10, freq = 'H'))
ts
ts_period = ts.to_period()
ts_period
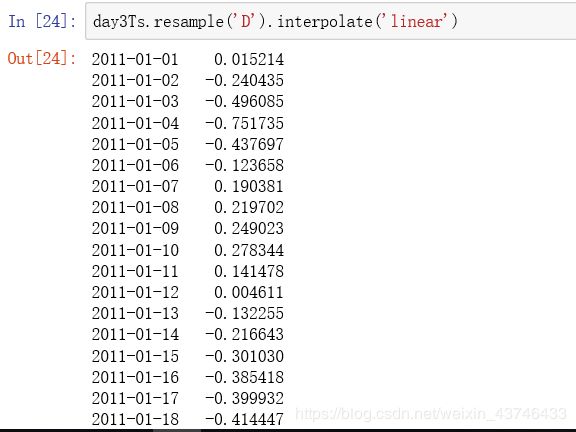
1.8 时间序列插值
插值方法:
2.股价预测(回归)
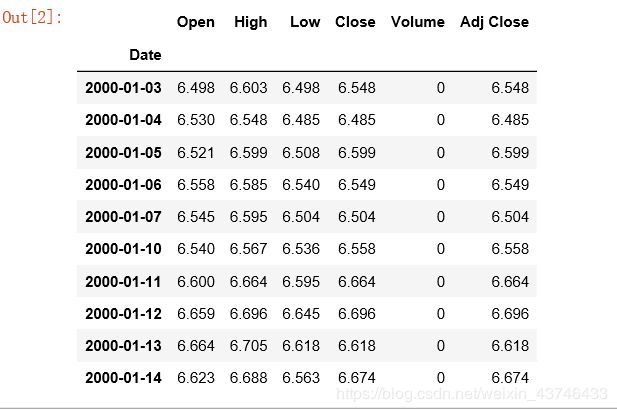
2.1 查看数据
import pandas as pd
import pandas_datareader
import datetime
import matplotlib.pylab as plt
import seaborn as sns
from matplotlib.pylab import style
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
style.use('ggplot')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
stockFile = 'data/T10yr.csv'
stock = pd.read_csv(stockFile, index_col=0, parse_dates=[0])
stock.head(10)
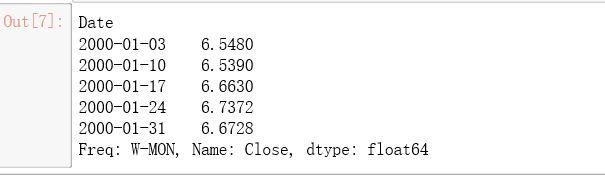
2.2 取Close列每周的平均值
stock_week = stock['Close'].resample('W-MON').mean()
stock_train = stock_week['2000':'2015']
stock_train.head()
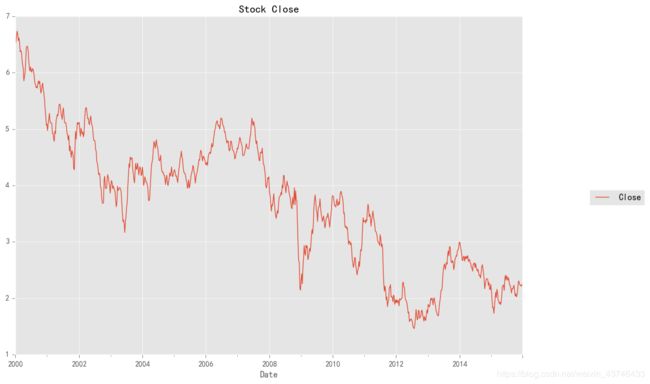
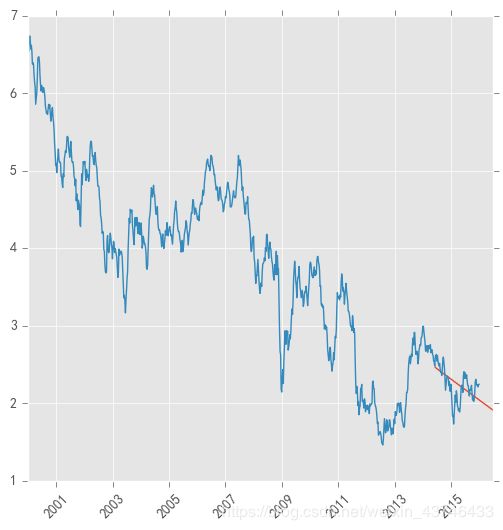
2.3 Close列每周的平均值绘制折线图
stock_train.plot(figsize=(12,8))
plt.legend(bbox_to_anchor=(1.25, 0.5))
plt.title("Stock Close")
sns.despine()
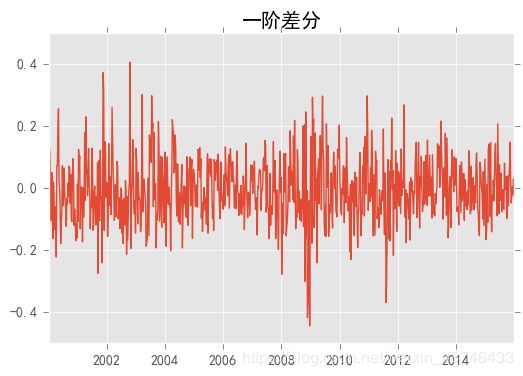
2.4 一阶分差,提高平稳性
stock_diff = stock_train.diff()
stock_diff = stock_diff.dropna()
plt.figure()
plt.plot(stock_diff)
plt.title('一阶差分')
plt.show()
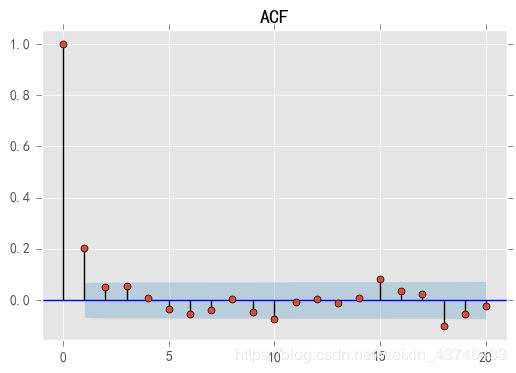
2.5 ACF,PACF
- 自相关函数ACF
有序的随机变量序列与其自身相比较
自相关函数反映了同一序列在不同时序的取值之间的相关性
acf = plot_acf(stock_diff, lags=20)
plt.title("ACF")
acf.show()
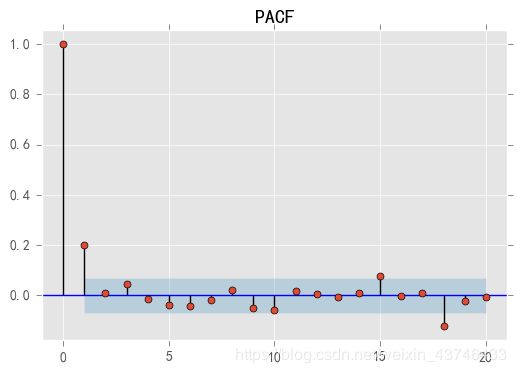
- 偏自相关函数(PACF)
对于一个平稳AR(p模型,求出滞后k自相关系数p(k)时,实际上得到并不是x(t)与x(t-k)之间单纯的相关关系。
x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的影响,而这k-1个随机变量又都和x(t-k)具有相关关系。
所以,自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响。
偏自相关函数,剔除了中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的干扰之后,x(t-k)对x(t)影响的相关程度。
ACF还包含了其他变量的影响。
PACF是严格这两个变量之间的相关性。
ACF包含了其他阶的影响
PCAF只包含这两阶的影响,更绝一些,把中间阶都剔除了
pacf = plot_pacf(stock_diff, lags=20)
plt.title("PACF")
pacf.show()
2.6 ARIMA模型
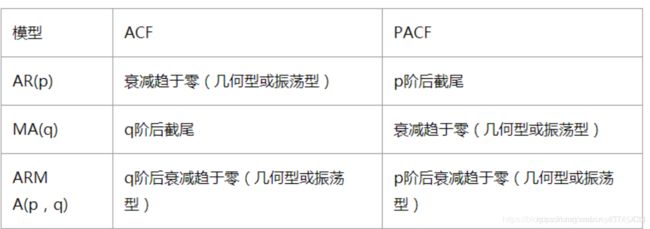
- 差分自回归移动平均模型 ARIMA(p,d,q)
自回归模型描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。 - AR是自回归, p为自回归项;
- MA为移动平均,q为移动平均项数,
- d为时间序列成为平稳时所做的差分次数
- 截尾:落在置信区间内(95%的点都符合该规则)
AR (p ) 看PACF
MA(q ) 看ACF - ACF中第几个点落到阴影面积中,就为第几阶p
- PACF中第几个点落到阴影面积中,就为第几阶q
model = ARIMA(stock_train, order=(1, 1, 1),freq='W-MON')
result = model.fit()
#print(result.summary())
pred = result.predict('20140609', '20160701',dynamic=True, typ='levels')
print (pred)
plt.figure(figsize=(6, 6))
plt.xticks(rotation=45)
plt.plot(pred)
plt.plot(stock_train)
2.7 总结
- ARIMA建模流程
(1)将序列平稳化(差分法确定d)
(2)p和q阶数确定(ACF,PACF)
(3)ARIMA(p,d,q)
3. 对tsfresh库中机器人执行失败数据集分类(二分类)
- tsfresh库文档地址 http://tsfresh.readthedocs.io/en/latest/text/quick_start.html
3.1 查看数据
import matplotlib.pylab as plt
import seaborn as sns
from tsfresh.examples.robot_execution_failures import download_robot_execution_failures, load_robot_execution_failures
from tsfresh import extract_features, extract_relevant_features, select_features
from tsfresh.utilities.dataframe_functions import impute
from tsfresh.feature_extraction import ComprehensiveFCParameters
from sklearn.tree import DecisionTreeClassifier
from sklearn.cross_validation import train_test_split
from sklearn.metrics import classification_report
download_robot_execution_failures()
df, y = load_robot_execution_failures()#导入tsfresh官网上例子数据
df.head()
3.2 绘制不同传感器的数据随时间变化
df[df.id == 3][['time', 'a', 'b', 'c', 'd', 'e', 'f']].plot(x='time', title='Success example (id 3)', figsize=(12, 6));
df[df.id == 20][['time', 'a', 'b', 'c', 'd', 'e', 'f']].plot(x='time', title='Failure example (id 20)', figsize=(12, 6));
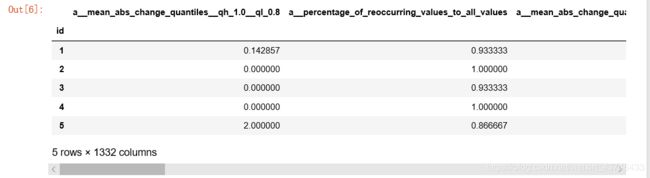
3.3 时间序列特征提取
extraction_settings = ComprehensiveFCParameters()
#column_id (str) – The name of the id column to group by
#column_sort (str) – The name of the sort column.
X = extract_features(df,
column_id='id', column_sort='time',
default_fc_parameters=extraction_settings,
impute_function= impute)
X.head()
- 特征过滤
X_filtered = extract_relevant_features(df, y,
column_id='id', column_sort='time',
default_fc_parameters=extraction_settings)
X_filtered.head()
3.4 用决策树模型训练,预测,评估
树模型参数:
-
1.criterion gini or entropy
-
2.splitter best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中(数据量大的时候)
-
3.max_features None(所有),log2,sqrt,N 特征小于50的时候一般使用所有的
-
4.max_depth 数据少或者特征少的时候可以不管这个值,如果模型样本量多,特征也多的情况下,可以尝试限制下
-
5.min_samples_split 如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
-
6.min_samples_leaf 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝,如果样本量不大,不需要管这个值,大些如10W可是尝试下5
-
7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。
-
8.max_leaf_nodes 通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制具体的值可以通过交叉验证得到。
-
9.class_weight 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。
-
10.min_impurity_split 这个值限制了决策树的增长,如果某节点的不纯度(基尼系数,信息增益,均方差,绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。
-
n_estimators:要建立树的个数
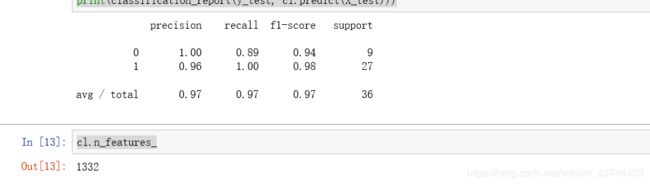
X_train, X_test, X_filtered_train, X_filtered_test, y_train, y_test = train_test_split(X, X_filtered, y, test_size=.4)
cl = DecisionTreeClassifier()
cl.fit(X_train, y_train)
print(classification_report(y_test, cl.predict(X_test)))
cl2 = DecisionTreeClassifier()
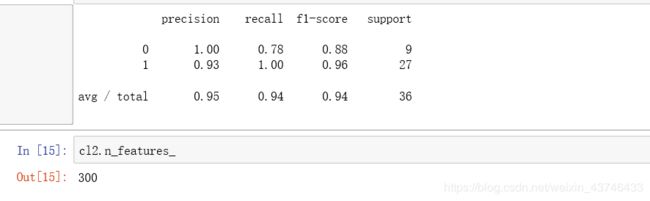
cl2.fit(X_filtered_train, y_train)
print(classification_report(y_test, cl2.predict(X_filtered_test)))
- 查看特征的重要性
pd.Series(rfr.feature_importances_, index = df.feature_names).sort_values(ascending = False)