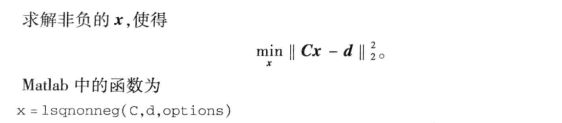美赛(matlab自学)之插值与拟合2
曲线拟合的线性最小二乘法
线性最小二乘法
matlab线性最小二乘的标准型为
![]()
命令为A=R\Y。
多项式拟合方法:
如果取![]()
,即用m次多项式拟合给定数据,maylab中有现成的函数
a=polyfit(x0,y0,m)
x0,y0为要拟合的数据;m为拟合的多项式的次数;输出参数a
![]()
多项式的值y可用y=polyval(a,x)计算
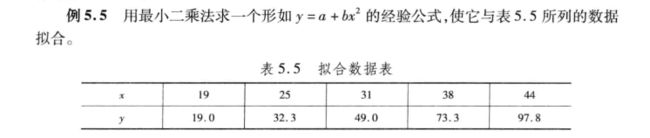
例题1
代码
x=[19 25 31 38 44]';
y=[19.0 32.3 49.0 73.3 97.8]';
r =[ones(5,1),x.^2];
ab=r\y
x0 =19:0.1:44;
y0 =ab(1) +ab(2) *x0.^2;
plot(x,y,'o',x0,y0,'r')
运行结果
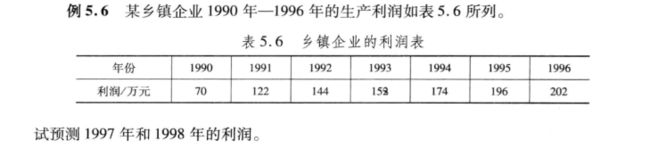
例题2
代码
解 作已知数据的散点图 ,有
x0 =[1990 1991 1992 1993 1994 1995 1996];
y0 =[70 122 144 152 174 196 202];
plot(x0,y0,' *')

发现该乡镇企业的年生产利润几乎直线上升。因此,可以用y=a1x +a0作为拟合函
数来预测该乡镇企业未来的年利润。
编写程序如下:
x0 =[1990 1991 1992 1993 1994 1995 1996] ;
y0=[70 122 144 152 174 196 202] ;
a =polyfit(x0,y0,1)
y97 = polyval(a,1997)
y98 = polyval(a,1998)
最小二乘法优化
在无约束最优化问题中,有些重要的特殊情形,比如目标函数由若干个函数的·平方和构成,这类函数一般可以写成

式中![]()
把极小化这类函数问题![]()
称为最小二乘优化问题。
函数工具箱
lsqlin函数

1: x = lsqlin(C,d,A,b) %求在约束条件 下,方程Cx = d
的最小二乘解x。
2:x = lsqlin(C,d,A,b,Aeq,beq) %Aeq、beq 满足等式约束 ,若没有不等式约
束,则设A=[ ],b=[ ]。
3:x = lsqlin(C,d,A,b,Aeq,beq,lb,ub) %lb、ub 满足 ,若没有等式约束,则
Aeq=[ ],beq=[ ]。
4:x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0) % x0 为初始解向量,若x 没有界,
则lb=[ ],ub=[ ]。
5:x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options) % options为指定优化参
数
lsqcurvefit函数
例题
在这里插入图片描述
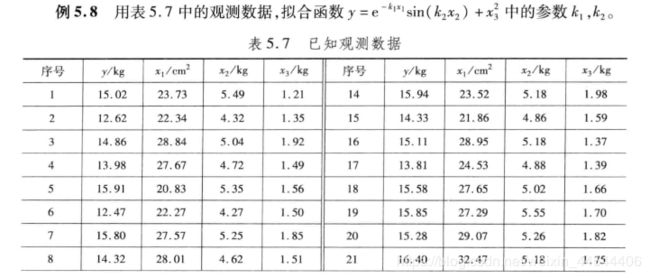
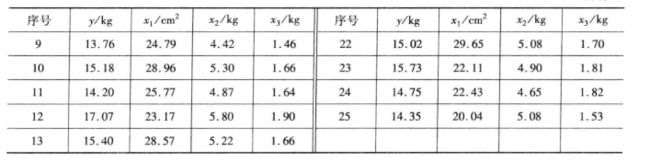
解
(1)编写M文件funl.m定义函数F(x,xdata)。
function f = fun1 ( canshu, xdata);
f= exp( - canshu(1) * xdata(:,1)). * sin( canshu(2) * xdata(:,2)) + xdata(:,3).^
2;%其中canshu(1) = k1 ,canshu(2) =k2,注意函数中自变量的形式
(2)把原始数据全部复制保存到纯文本文件data1. txt中,包括13行后面的空行。
调用函数lsqcurvefit, 编写程序如下:
clc, clear
a = textread( 'data1.txt');
y0 =a(:,[2,7]); %提出因变量y的数据
y0 = nonzeros(y0);%去掉最后的0元素,且变成列向量
x0 =[a(:,[3:5]);a([1:end-1],[8:10])];%由分块矩阵构造因变量数据的3列矩阵
canshu0 = rand(2,1); %拟合参数的初始值是任意取的.
%非线性拟合的答案是不唯一的,下面给出拟合参数的上下界
1b=zeros(2,1);%这里是随意给的拟合参数的下界,无下界时,默认值是空矩阵[ ]
ub=[20;2];%这里是随意给的上界,无上界时,默认值是空矩阵[ ]
canshu = lsqcurvefit(@ fun1 , canshu0 ,x0 ,y0 ,1b,ub)
clc,clear
load data3%分别加载xi的观测值x0,yi的观测值y0
mf =@ (cs,xdata)1 /sqrt(2 *pi) /cs(2) *exp( - ( xdata -cs(1)).^2 /cs(2)^2/2);
%yc=mf([2,1],1)%测试匿名函数
cs = lsqcurvefit(mf,rand(2,1),x0,y0)%拟合参数的初始值是任意取的
lsqnonlin函数
clc, clear
load data3 %分别加载xi的观测值x0,yi的观测值y0
F=@ (cs) 1 /sqrt(2 *pi) /cs(2) *exp( -(x0 -cs(1)).*2/cs(2)^2/2) -y0;
cs0 =rand(2,1);%拟合参数的初始值是任意取的
cs = lsqnonlin(F ,cs0)