Java实现八种排序算法及其原理(一)
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序算法,就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范,要得到一个符合实际的优秀算法,得经过大量的推理和分析。
排序(Sorting) 是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个关键字有序的序列。其实就是把集合中的元素按照一定的次序排序在一起,其中有八种基本排序:
1、冒泡排序
把较小的元素往前调或者把较大的元素往后调。这种方法主要是通过对相邻两个元素进行大小的比较,根据比较结果和算法规则对该元素的位置进行交换,这样逐个依次进行比较和交换,就能达到排序目的。冒泡排序的基本思想是,首先将第1个和第2个记录的关键字比较大小,如果是逆序的,就将这两个记录进行交换,再对第2个和第3个记录的关键字进行比较,依次类推,重复进行上述计算,直至完成第(n一1)个和第n个记录的关键字之间的比较,此后,再按照上述过程进行第2次、第3次排序,直至整个序列有序为止。排序过程中要特别注意的是,当相邻两个元素大小一致时,这一步操作就不需要交换位置,因此也说明冒泡排序是一种严格的稳定排序算法,它不改变序列中相同元素之间的相对位置关系。
代码实现:
public class BubbleSort {
public static void sort(int[] array){
if(array == null || array.length == 0){
return;
}
int a = array.length;
//外层:需要a-1次循环比较
for (int i = 0; i < a - 1; i++) {
//内层:每次循环需要两两比较的次数,每次比较后,都会将当前最大的数放到最后位置,所以每次比较次数递减一次
if (array[i] > array[i + 1]) {
//交换数组array的i和i+1位置的数据
swap(array, i, i+1);
}
}
}
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
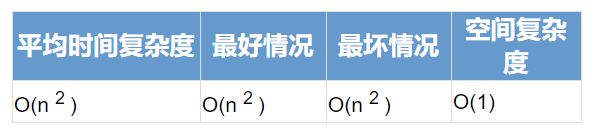
}冒泡排序是稳定的排序算法,最容易实现的排序, 最坏的情况是每次都需要交换, 共需遍历并交换将近n²/2次, 时间复杂度为 O(n²). 最佳的情况是内循环遍历一次后发现排序是对的, 因此退出循环, 时间复杂度为O(n). 平均来讲, 时间复杂度为O(n²). 由于冒泡排序中只有缓存的temp变量需要内存空间 , 因此空间复杂度为常量O(1)。
其中交换数字主要有三种方法:临时变量法、算术法、位运算法,代码如下:
public class Demo {
public static void main(String[] args) {
// 临时变量法
int[] array = new int[]{10, 20};
System.out.println(Arrays.toString(array));
swapByTemp(array, 0, 1);
System.out.println(Arrays.toString(array));
// 算术法
array = new int[]{10, 20};
swapByArithmetic(array, 0, 1);
System.out.println(Arrays.toString(array));
// 位运算法
array = new int[]{10, 20};
swapByBitOperation(array, 0, 1);
System.out.println(Arrays.toString(array));
}
//临时变量法:交换数组array的i和j位置的数据
public static void swapByTemp(int[] array, int i, int j){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
//算术交换:交换数组array的i和j位置的数据(有可能溢出)
public static void swapByArithmetic(int[] array, int i, int j) {
array[i] = array[i] + array[j];
array[j] = array[i] - array[j];
array[i] = array[i] - array[j];
}
//位运算法:交换数组array的i和j位置的数据
public static void swapByBitOperation(int[] array, int i, int j) {
array[i] = array[i]^array[j];
array[j] = array[i]^array[j];
array[i] = array[i]^array[j];
}
}2、选择排序
为每一个位置选择当前最小的元素。选择排序的基本思想是,基于直接选择排序和堆排序这两种基本的简单排序方法。首先从第1个位置开始对全部元素进行选择,选出全部元素中最小的给该位置,再对第2个位置进行选择,在剩余元素中选择最小的给该位置即可;以此类推,重复进行“最小元素”的选择,直至完成第(n-1)个位置的元素选择。使用这种排序时,要注意其中一个不同于冒泡法的细节。举例说明:序列58539.我们知道第一遍选择第1个元素“5”会和元素“3”交换,那么原序列中的两个相同元素“5”之间的前后相对顺序就发生了改变。因此,选择排序不是稳定的排序算法,它在计算过程中会破坏稳定性。
代码实现:
public class SelectionSort {
public static void sort(int[] array){
for (int i = 0; i < array.length - 1; i++) {
int min = i;
for (int j = i+1; j < array.length; j ++) { //选出之后待排序中值最小的位置
if (array[j] < array[min]) {
min = j;
}
}
if (min != i) {
array[min] = array[i] + array[min];
array[i] = array[min] - array[i];
array[min] = array[min] - array[i];
}
}
}
}不稳定排序算法,选择排序的简单和直观名副其实,这也造就了它出了名的慢性子,无论是哪种情况,哪怕原数组已排序完成, 它也将花费将近n²/2次遍历来确认一遍。 唯一值得高兴的是,它并不耗费额外的内存空间。
3、插入排序
基于某序列已经有序排列的情况下,通过一次插入一个元素的方式按照原有排序方式增加元素。这种比较是从该有序序列的最末端开始执行,即要插入序列中的元素最先和有序序列中最大的元素比较,若其大于该最大元素,则可直接插入最大元素的后面即可,否则再向前一位比较查找直至找到应该插入的位置为止。插入排序的基本思想是,每次将1个待排序的记录按其关键字大小插入到前面已经排好序的子序列中,寻找最适当的位置,直至全部记录插入完毕。执行过程中,若遇到和插入元素相等的位置,则将要插人的元素放在该相等元素的后面,因此插入该元素后并未改变原序列的前后顺序。插入排序也是一种稳定的排序方法。插入排序分直接插入排序、折半插入排序和希尔排序3类。
(1)、直接插入排序:将数组中的所有元素依次跟前面已经排好的元素相比较,如果选择的元素比已排序的元素小,则交换,直到全部元素都比较过为止。其中包括两种写法:移位法和交换法。
移位法:完全按照以上算法描述,再插入过程中将有序序列中比待插入数字大的数据向后移动,由于移动时会覆盖待插入数据,所以需要额外的临时变量保存待插入数据:
public static void sort(int[] a) {
if (a == null || a.length == 0) {
return;
}
for (int i = 1; i < a.length; i++) {
int j = i - 1;
int temp = a[i]; // 先取出待插入数据保存,因为向后移位过程中会把覆盖掉待插入数
while (j >= 0 && a[j] > a[i]) { // 如果待是比待插入数据大,就后移
a[j+1] = a[j];
j--;
}
a[j+1] = temp; // 找到比待插入数据小的位置,将待插入数据插入
}
}交换法:不需要额外的保存待插入数据,通过不停的向前交换带插入数据,类似冒泡法,直到找到比它小的值,也就是待插入数据找到了自己的位置:
public static void sort(int[] a) {
if (a == null || a.length == 0) {
return;
}
for (int i = 1; i < a.length; i ++) {
int j = i - 1;
while (j >= 0 && a[j] > a[i]) {
a[j + 1] = a[j] + a[j+1]; //只要大就交换操作
a[j] = a[j + 1] - a[j];
a[j + 1] = a[j + 1] - a[j];
System.out.println("Sorting: " + Arrays.toString(a));
}
}
}直接插入排序不是稳定的排序算法:
(2)、折半插入排序:由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
代码实现:
public class BinaryInsertSort {
public static void main(String[] args) {
// 待排序的数组
int[] array = { 1, 0, 2, 5, 3, 4, 9, 8, 10, 6, 7 };
binaryInsertSort(array);
// 显示排序后的结果。
System.out.print("排序后: ");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
private static void binaryInsertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int low = 0;
int high = i - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (temp < array[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
for (int j = i; j >= low + 1; j--) {
array[j] = array[j - 1];
}
array[low] = temp;
}
}
}(3)、希尔排序:也称递减增量排序算法,先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录
“基本有序”时,再对全体记录进行依次直接插入排序。
代码实现:
public class ShellSort {
public static void sort(int[] arr) {
int gap = arr.length / 2;
for (;gap > 0; gap = gap/2) {
for (int j = 0; (j + gap) < arr.length; j++) { //不断缩小gap,直到1为止
for (int k = 0; (k + gap) < arr.length; k+=gap) { //使用当前gap进行组内插入排序
if (arr[k] > arr[k+gap]) { //交换操作
arr[k] = arr[k] + arr[k+gap];
arr[k+gap] = arr[k] - arr[k+gap];
arr[k] = arr[k] - arr[k+gap];
System.out.println(" Sorting: " + Arrays.toString(arr));
}
}
}
}
}
}未完待续:https://blog.csdn.net/weixin_44544465/article/details/97492664