最大流,最小费用最大流:解析 + 各种板子
网络流初步 + Edmond-Karp算法
网络流的基本概念
- 源点,这个点只有流量的流出,没有流入。
- 汇点,这个点只有流量的流入,没有流出。
- 容量,每条有向边的最大可承受的流的理论大小。
- 流量,每条有向边的最大可承受的流的实际大小。
- 最大流,从源点可流入汇点的最大流量。
Edmond-Karp算法
1、如果可以找到增广的路径,取这条路径上的最小的容量作为当前的可增广的流量。
2、在这条增广的路径中的每一个有向边减去当前可增广的流量,同时在其反向边加上当前可增广的流量。
3、重复1的操作,如果不能找到可增广的路径,则说明,已经找到了最大流,输出答案即可。
为什么要在反向边上增加上当前可增广的流量。
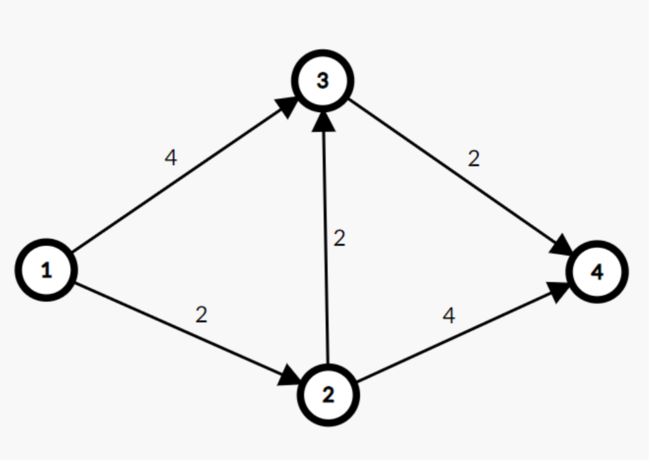
毫无疑问这张图的最大流是 4 = 2 ( 1 − > 3 − > 4 ) + 2 ( 1 − > 2 − > 4 ) 4 = 2(1 -> 3 -> 4) + 2(1 -> 2 -> 4) 4=2(1−>3−>4)+2(1−>2−>4)
但是如果我们找寻的一条增广路径是 2 ( 1 − > 2 − > 3 − > 4 ) 2(1 -> 2 -> 3 -> 4) 2(1−>2−>3−>4)之后,我们再也就找不到其他的增广路径了
但是如果我们在每一次取用这条边之后,在其反方向增加对应的反向边。
显然我们可以得到另一个增广路径 2 ( 1 − > 3 − > 2 − > 4 ) 2(1 -> 3 -> 2 -> 4) 2(1−>3−>2−>4),这里我们得到的最大流,也是正确答案。
板子 + 例题
Flow Problem 题目链接
#include
using namespace std;
const int INF = 0x3f3f3f3f;
int maze[20][20], n, m;
int visit[20], pre[20];
bool bfs(int st, int ed) {
queue q;
memset(visit, 0, sizeof visit);
q.push(st);
visit[st] = 1;
while(!q.empty()) {
int temp = q.front();
q.pop();
if(temp == ed) return true;
for(int i = 1; i <= n; i++) {
if(!visit[i] && maze[temp][i] > 0) {
visit[i] = 1;
q.push(i);
pre[i] = temp;
}
}
}
return false;
}
int max_flow(int st, int ed) {
int ans = 0;
while(bfs(st, ed)) {
int now_max = INF;
int p = ed;
while(p != st) {
now_max = min(now_max, maze[pre[p]][p]);
p = pre[p];
}
p = ed;
while(p != st) {
maze[pre[p]][p] -= now_max;
maze[p][pre[p]] += now_max;
p = pre[p];
}
ans += now_max;
}
// cout << ans << endl;
return ans;
}
int main() {
// freopen("in.txt", "r", stdin);
int t, x, y, w;
scanf("%d", &t);
for(int cas = 1; cas <= t; cas++) {
scanf("%d %d", &n, &m);
memset(maze, 0, sizeof maze);
for(int i = 0; i < m; i++) {
scanf("%d %d %d", &x, &y, &w);
maze[x][y] += w;
}
printf("Case %d: %d\n", cas, max_flow(1, n));
}
return 0;
}
最大流
Edmond-Karp
原版的是用邻接矩阵写的,太耗内存了,这里改成邻接表。
#include
using namespace std;
const int N1 = 1e4 + 10, N2 = 2e5 + 10;
const int INF = 0x3f3f3f3f;
int head[N1], to[N2], nex[N2], cap[N2], cnt;
int flow[N1], pre[N1], id[N1], n, m, s, t;
void add(int x, int y, int w) {
to[cnt] = y;
nex[cnt] = head[x];
cap[cnt] = w;
head[x] = cnt++;
}
void input() {
scanf("%d %d %d %d", &n, &m, &s, &t);
int x, y, w;
for(int i = 0; i < m; i++) {
scanf("%d %d %d", &x, &y, &w);
add(x, y, w);
add(y, x, 0);
}
}
void init() {
memset(head, -1, sizeof head);
cnt = 0;
}
int max_flow() {
int ans = 0;
for(;;) {
queue q;
memset(flow, 0, sizeof flow);
flow[s] = INF;
q.push(s);
while(!q.empty()) {
int temp = q.front();
q.pop();
for(int i = head[temp]; ~i; i = nex[i]) {
if(!flow[to[i]] && cap[i] > 0) {
flow[to[i]] = min(flow[temp], cap[i]);
pre[to[i]] = temp;
id[to[i]] = i;
q.push(to[i]);
}
}
if(flow[t]) break;
}
if(!flow[t]) break;
int p = t;
while(p != s) {
cap[id[p]] -= flow[t];
cap[id[p] ^ 1] += flow[t];
p = pre[p];
}
ans += flow[t];
}
return ans;
}
int main() {
// freopen("in.txt", "r", stdin);
init();
input();
printf("%d\n", max_flow());
return 0;
}
Dinic
玄学的Dinic
#include
using namespace std;
typedef long long ll;
const int N1 = 1e4 + 10, N2 = 2e5 + 10;
const int INF = 0x3f3f3f3f;
int head[N1], to[N2], nex[N2], cap[N2], cnt;
int now[N1];
int dis[N1], n, m, s, t;
void init() {
memset(head, -1, sizeof head);
cnt = 0;
}
void add(int x, int y, int w) {
to[cnt] = y;
nex[cnt] = head[x];
cap[cnt] = w;
head[x] = cnt++;
}
bool bfs() {
memset(dis, -1, sizeof dis);
queue q;
q.push(s);
dis[s] = 0;
now[s] = head[s];
while(!q.empty()) {
int temp = q.front();
q.pop();
if(temp == t) return true;
for(int i = head[temp]; ~i; i = nex[i]) {
if(dis[to[i]] == -1 && cap[i]) {
now[to[i]] = head[to[i]];
dis[to[i]] = dis[temp] + 1;
q.push(to[i]);
}
}
}
return false;
}
ll dfs(int rt, ll f) {
if(rt == t) return f;
ll delta = f;
for(int i = now[rt]; ~i; i = nex[i]) {
now[rt] = i;
if(dis[to[i]] == dis[rt] + 1) {
int temp = dfs(to[i], min(delta, 1ll * cap[i]));
cap[i] -= temp;
cap[i ^ 1] += temp;
delta -= temp;
}
if(delta == 0) break;
}
return f - delta;
}
ll Dinic() {
ll ans = 0;
while(bfs()) ans += dfs(s, 0x3f3f3f3f3f3f3f3f);
return ans;
}
int main() {
// freopen("in.txt", "r", stdin);
init();
scanf("%d %d %d %d", &n, &m, &s, &t);
int x, y, w;
for(int i = 0; i < m; i++) {
scanf("%d %d %d", &x, &y, &w);
add(x, y, w);
add(y, x, 0);
}
printf("%lld\n", Dinic());
return 0;
}
最小费用最大流
SPFA
#include
using namespace std;
const int N1 = 5e3 + 10, N2 = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int head[N1], to[N2], nex[N2], cap[N2], value[N2], cnt;
int dis[N1], pre[N1], id[N1], flow[N1], visit[N1], n, m, s, t;
void add(int x, int y, int f, int w) {
to[cnt] = y;
nex[cnt] = head[x];
value[cnt] = w;
cap[cnt] = f;
head[x] = cnt++;
}
bool spfa() {
memset(visit, 0, sizeof visit);
memset(dis, 0x3f, sizeof dis);
queue q;
q.push(s);
dis[s] = 0, visit[s] = 1, flow[s] = INF, pre[t] = -1;
while(!q.empty()) {
int temp = q.front();
q.pop();
visit[temp] = 0;
for(int i = head[temp]; ~i; i = nex[i]) {
if(cap[i] > 0 && dis[to[i]] > dis[temp] + value[i]) {
dis[to[i]] = dis[temp] + value[i];
flow[to[i]] = min(flow[temp], cap[i]);
pre[to[i]] = temp;
id[to[i]] = i;
if(!visit[to[i]]) {
q.push(to[i]);
visit[to[i]] = 1;
}
}
}
}
return pre[t] != -1;
}
int min_cost_and_max_flow() {
int max_flow = 0, min_cost = 0;
while(spfa()) {
max_flow += flow[t];
min_cost += flow[t] * dis[t];
int p = t;
while(p != s) {
cap[id[p]] -= flow[t];
cap[id[p] ^ 1] += flow[t];
p = pre[p];
}
}
printf("%d %d\n", max_flow, min_cost);
}
void init() {
memset(head, -1, sizeof head);
cnt = 0;
}
int main() {
// freopen("in.txt", "r", stdin);
init();
scanf("%d %d %d %d", &n, &m, &s, &t);
int x, y, f, w;
for(int i = 0; i < m; i++) {
scanf("%d %d %d %d", &x, &y, &f, &w);
add(x, y, f, w);
add(y, x, 0, -w);
}
min_cost_and_max_flow();
return 0;
}
两个假的Dijkstra
洛谷模板题卡爆DIjkstra。
好像第一个稍优一点。
第一个假的Dijkstra
#include
#define mp make_pair
#define pb push_back
#define x first
#define y second
using namespace std;
typedef pair PII;
const int N1 = 5e3 + 10;
const int INF = 0x3f3f3f3f;
int dis[N1], h[N1], flow[N1], pre[N1], id[N1], visit[N1], n, m, s, t;
struct Edge {
int to, cap, value, rever;
Edge(int _to, int _cap, int _value, int _rever) : to(_to), cap(_cap), value(_value), rever(_rever) {}
};
vector G[N1];
void add(int x, int y, int f, int w) {
Edge temp1 = Edge(y, f, w, G[y].size());
Edge temp2 = Edge(x, 0, -w, G[x].size());
G[x].pb(temp1);
G[y].pb(temp2);
}
int min_cost_and_max_flow() {
int min_cost = 0, max_flow = 0;
memset(dis, 0x3f, sizeof dis);
for(;;) {
priority_queue, greater > q;
dis[s] = 0, flow[s] = INF;
q.push(mp(0, s));
while(!q.empty()) {
PII temp = q.top();
q.pop();
if(visit[temp.y]) continue;
visit[temp.y] = 1;
int u = temp.y;
for(int i = 0; i < G[u].size(); i++) {
Edge v = G[u][i];
if(v.cap > 0 && dis[v.to] > dis[u] + v.value + h[u] - h[v.to]) {
dis[v.to] = dis[u] + v.value + h[u] - h[v.to];
flow[v.to] = min(v.cap, flow[u]);
pre[v.to] = u;
id[v.to] = i;
q.push(mp(dis[v.to], v.to));
}
}
}
if(visit[t] == 0) break;
max_flow += flow[t];
for(int i = 1; i <= n; i++) {
h[i] += dis[i];
dis[i] = INF;
visit[i] = 0;
}
min_cost += flow[t] * h[t];
int p = t;
while(p != s) {
G[pre[p]][id[p]].cap -= flow[t];
G[p][ G[pre[p]][id[p]].rever].cap += flow[t];
p = pre[p];
}
}
printf("%d %d\n", max_flow, min_cost);
}
int main() {
// freopen("in.txt", "r", stdin);
scanf("%d %d %d %d", &n, &m, &s, &t);
int x, y, f, w;
for(int i = 0; i < m; i++) {
scanf("%d %d %d %d", &x, &y, &f, &w);
add(x, y, f, w);
}
min_cost_and_max_flow();
return 0;
}
第二个假的Dijkstra
#include
#define mp make_pair
using namespace std;
typedef pair PII;
const int N1 = 5e3 + 10, N2 = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int head[N1], to[N2], nex[N2], cap[N2], value[N2], cnt;
int visit[N1], flow[N1], dis[N1], pre[N1], id[N1], h[N1], n, m, s, t;
void init() {
memset(head, -1, sizeof head);
cnt = 0;
}
void add(int x, int y, int f, int w) {
to[cnt] = y;
nex[cnt] = head[x];
value[cnt] = w;
cap[cnt] = f;
head[x] = cnt++;
}
int min_cost_and_max_flow() {
int min_cost = 0, max_flow = 0;
memset(dis, 0x3f, sizeof dis);
for(;;) {
priority_queue, greater > q;
q.push(mp(0, s));
flow[s] = INF, dis[s] = 0;
while(!q.empty()) {
int temp = q.top().second;
q.pop();
// if(temp == t) break;
if(visit[temp]) continue;
visit[temp] = 1;
// if(temp == t) break;
for(int i = head[temp]; ~i; i = nex[i]) {
if(cap[i] > 0 && dis[to[i]] > dis[temp] + value[i] + h[temp] - h[to[i]]) {
dis[to[i]] = dis[temp] + value[i] + h[temp] - h[to[i]];
flow[to[i]] = min(flow[temp], cap[i]);
pre[to[i]] = temp;
id[to[i]] = i;
q.push(mp(dis[to[i]], to[i]));
}
}
}
if(visit[t] == 0) break;
for(int i = 1; i < n; i++) {
h[i] += dis[i];
visit[i] = 0;
dis[i] = INF;
}
max_flow += flow[t];
min_cost += flow[t] * h[t];
int p = t;
while(p != s) {
cap[id[p]] -= flow[t];
cap[id[p] ^ 1] += flow[t];
p = pre[p];
}
}
printf("%d %d\n", max_flow, min_cost);
}
int main() {
// freopen("in.txt", "r", stdin);
init();
scanf("%d %d %d %d", &n, &m, &s, &t);
int x, y, f, w;
for(int i = 0; i < m; i++) {
scanf("%d %d %d %d", &x, &y, &f, &w);
add(x, y, f, w);
add(y, x, 0, -w);
}
min_cost_and_max_flow();
return 0;
}