2020 牛客多校暑期第二场

ps:用来监督自己补题

F Fake Maxpooling
题意:给一个nm的矩阵，求所有kk的子矩阵中最大值的的和

思路：
横竖两遍单调队列就秒了，一瞬间就想到了，但是O(n*m log)以为铁T，看到还以为是数学题，就打表找了很久规律，结果过的人越来越多，就上去秒了

学到了出题人一个很牛掰的方法，具体思路其实就是和欧拉筛一样，筛倍数，是O(nm loglog),这样就比较稳了，其实应该是可以线性筛O(nm)，只是比较麻烦而已

#include

using namespace std;
typedef long long ll;
const int maxn=5005;
int a[maxn][maxn],q[maxn],head,tail,f[maxn][maxn];
int gcd(int a,int b){return  b?gcd(b,a%b):a;}
int main()
{
   int n,m,k;
   scanf("%d%d%d",&n,&m,&k); 
   for(int i=1;i<=n;++i)
      for(int j=1;j<=m;++j)
          if(!a[i][j])
              for(int k=1;k*i<=n&&k*j<=m;++k)
                  a[k*i][k*j]=k;
   for(int i=1;i<=n;++i)
       for(int j=1;j<=m;++j)
           a[i][j]=i*j/a[i][j];
   int cnt=0; 
   for(int j=1;j<=m;++j)
   {
      cnt=0; 
      head=1,tail=0;
      for(int i=1;i<=n;++i)
      {   
          while(head<=tail&&a[i][j]>=a[q[tail]][j])tail--;
          q[++tail]=i;
          if(i-q[head]+1>k)head++;
          if(i>=k)f[++cnt][j]=a[q[head]][j];
      } 
   } 
   ll ans=0;
   for(int i=1;i<=cnt;++i)
   {
      head=1,tail=0;
      for(int j=1;j<=m;++j)
      {
         while(head<=tail&&f[i][j]>=f[i][q[tail]])tail--;
         q[++tail]=j;
         if(j-q[head]+1>k)head++;
         if(j>=k)ans+=f[i][q[head]]; 
      } 
   }
   printf("%lld\n",ans);
   return 0; 
}

G.Greater and Greater

题意：给出两个序列 A、B，其长度分别为 n、m，保证 n>m ，求 A 中有多少个长度为 m 的子串 S，使得∀i∈{1,2,⋯,m},Si≥Bi

思路：
这题我补了很久，尽量用通俗的语言讲，首先对于每个Ai维护一个长度为bitset，Si[j]=1当且仅当Ai>=Bj,如下图，我们发现，其实本质只有m+1种这样的bitset，他们取决于该数字在排序后的数字的位置，对B排序后的bitset Si我们可以发现，Si+1和第Si唯一的差别就是在对应的原来的id的位置设置为1

这样我们很容易可以预处理出所有Si,那么怎么求出ans呢，如下图，发现当一竖列都为1的时候，可以对答案贡献，所以我们只需要倒序将si不断左移并且&上s(i-1)即可，具体来说，就是用一个curi,


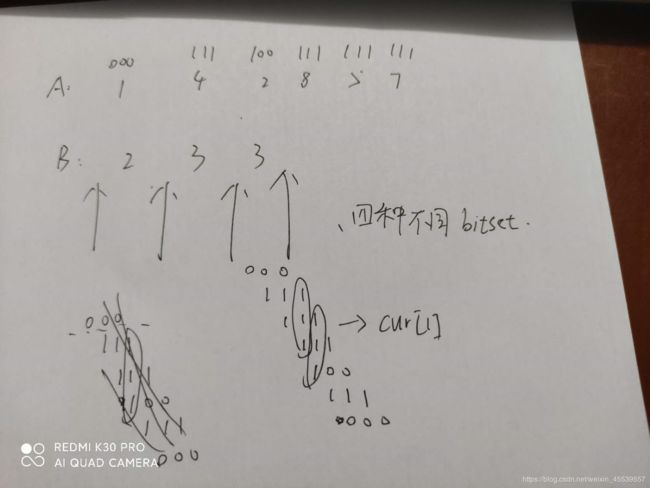
为什么要或上第m位为1的数呢，因为左移的时候，是为了防止后面的数不被影响，即只受所&的数的影响，还要吐槽一句，我从没用过bitset，这里的左移，居然是>>,调了我4h

H.Happy Triangle

题意：给你一个multiset，三种操作
1.加入x
2.删去x
3.给出一个x，问能否在multiset中找到另外两个元素a,b，a可以等于b，使得三者可以构成一个非退化三角形

思路：
假设a<=b,则x可能是最大值，次大值，最小值
1.如果是最大值的话，只需要<=x的最大的两个a,b可以就行了
2.如果是次大值，则x加上x的前驱>x的后缀就行了
3.最小值的话，只需要abs|a-b|

我们来捋一捋，我们需要一个数据结构，支持增删，查找集合中的相邻的数最小值，根据增删单点修改最小值，不难想到，只要离散化+权值线段树即可，树上维护相邻的最小差值，我是转为离线操作再处理

#include
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define ls p<<1
#define rs p<<1|1
using namespace std;
multiset<int>s;
const int maxn=2e5+7;
const int inf=2e9+5;
const int INF=0x3f3f3f3f;
int tr[maxn<<2],op[maxn],a[maxn],b[maxn],q,cnt[maxn];
void build(int p,int l,int r)
{//一开始初始化为最大值
    tr[p]=inf;
    if(l==r)return;
    int mid=l+r>>1;
    build(lson);
    build(rson); 
}
void update(int p,int l,int r,int pos,int val)
{
    if(l==r){ 
        tr[p]=val;
        return;    
    } 
    int mid=l+r>>1;
    if(pos<=mid)update(lson,pos,val);
    else update(rson,pos,val);
    tr[p]=min(tr[ls],tr[rs]);
}
int query(int p,int l,int r,int L,int R)
{
    if(L<=l&&r<=R)return tr[p];
    int mid=l+r>>1,ans1=inf,ans2=inf;
    if(L<=mid)ans1=query(lson,L,R);
    if(R>mid)ans2=query(rson,L,R);
    return min(ans1,ans2); 
}
int main()
{
    s.insert(-INF);s.insert(-INF);//正负无穷作为哨兵
    s.insert(inf);
    scanf("%d",&q);
    for(int i=1;i<=q;++i)
        scanf("%d%d",&op[i],&a[i]),b[i]=a[i];
    sort(a+1,a+1+q);
    int len=unique(a+1,a+1+q)-(a+1);
    build(1,1,len);
    for(int i=1;i<=q;++i)
    {
        if(op[i]==1){ 
            s.insert(b[i]);
            int x=lower_bound(a+1,a+1+len,b[i])-a;
            cnt[x]++;
            if(cnt[x]==1){//只有一个的时候是上一个和当前的差值
                update(1,1,len,x,*s.upper_bound(b[i])-b[i]);
                auto it=s.lower_bound(b[i]);
                it--;  
                int tmp=*it;
                int y=lower_bound(a+1,a+1+len,tmp)-a;
                if(cnt[y]==1)update(1,1,len,y,b[i]-tmp);//只有上一个数只剩一个的时候才更新
            } 
            else if(cnt[x]==2)update(1,1,len,x,0);//因为如果超过1个，最小差值肯定是0
        } 
        else if(op[i]==2) {
            s.erase(s.find(b[i]));
            int x=lower_bound(a+1,a+1+len,b[i])-a;
            cnt[x]--;
            if(cnt[x]==1)update(1,1,len,x,*s.upper_bound(b[i])-b[i]);//删到只剩一个的时候更新
            else if(!cnt[x]){ //删没的时候要更新前面那个
                update(1,1,len,x,inf);
                auto it=s.lower_bound(b[i]);
                it--;
                int tmp=*it;
                int y=lower_bound(a+1,a+1+len,tmp)-a;
                if(cnt[y]==1)update(1,1,len,y,*s.lower_bound(b[i])-tmp);
            }
        } 
        else{ 
            bool flag=0;
            auto it=s.lower_bound(b[i]);
            int t1=*it,t2=*(--it),t3=*(--it);
            int x=lower_bound(a+1,a+1+len,b[i])-a;
            if(t2+t3>b[i]||t2+b[i]>t1)flag=1;//判断第一种和第二种能否成三角形
            if(query(1,1,len,x,len)<b[i])flag=1;//第三种查询最小差值
            if(flag)puts("Yes");
            else puts("No"); 
        }
    }
    return 0; 
}

J.Just Shuffle

题意：
初始是1 2…n，给你一个置换函数 f^k之后得到的数列，问 f 是什么，继续背锅…一开始我记得我的置换定义是没有错的，但是自己傻叉了手推样例的时候推不对，以为自己错了，结果听老板搞了个错的题意，居然还可以推出来样例，后面自闭3h推不出，一开始我就往同余想了，结果自己sb手写样例还算错，无语了

思路：
首先得搞懂置换是什么东西，其实可以看成是一一映射，举例来说，如下图。

知道置换是什么东西就好搞了，事实上，对于一个置换，我们会产生一些环，也就是经过一段周期后回到初始位置，我们设答案 F这个函数形成的环的 size分别为 sz1,sz2…我们发现，其实我们已知F走k到达的点，现在求每个点走第一步到达的点，由于k是个大质数，所以有以下做法

简单来说就是在F^k上走inv(k,size (F ^k))步走到的地方就等于答案，所以根据输入构造下环求个逆元就秒了

#include
#define pb push_back
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
int a[maxn],ans[maxn],x,y;
bool v[maxn];
int exgcd(int a,int b,int &x,int &y){
   if(!b){ x=1,y=0;return a;}
   int d=exgcd(b,a%b,x,y);
   int z=x;x=y;y=z-y*(a/b);
   return d; 
}
int inv(int k,int size){
    exgcd(k,size,x,y);
    return (x%size+size)%size;
}
int main()
{ 
   int n,k;
   scanf("%d%d",&n,&k);
   for(int i=1;i<=n;++i)
      scanf("%d",&a[i]);
   for(int i=1;i<=n;++i){
      if(v[i])continue;
      vector<int>tmp;
      tmp.pb(i);v[i]=1;
      int now=a[i];
      while(now!=i){ 
          tmp.pb(now);v[now]=1;
          now=a[now];  
      } 
      int sz=tmp.size();
      int ni=inv(k,sz);
      for(int i=0;i<sz;++i)
         ans[tmp[i]]=tmp[(i+ni)%sz]; 
   } 
   for(int i=1;i<=n;++i)
       printf("%d ",ans[i]);
   return 0; 
}