支持向量机SVM(3)-非线性支持向量机与核函数

非线性支持向量机与核函数

本节包括以下内容

• 1.非线性分类问题
• 2.核函数的定义
• 3.核技巧在支持向量机中的应用
• 4.正定核    \; 核心问题:函数$K(x,z)$满足什么条件才能称为核函数？
• 5.常用核函数
• 6.非线性支持向量机学习算法

1.非线性分类问题

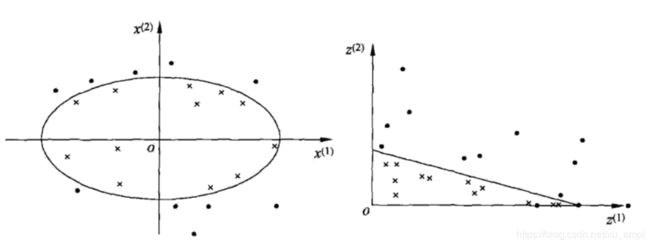
非线性分类问题是指通过利用非线性模型才能很好地进行分类的问题。下图是一个例子，下图的左图是一个分类问题，由下图可见，无法用直线(线性模型)将正负实例正确分开，但可以用一条椭圆曲线(非线性模型将它们正确分开)。
对于给定的一个训练数据集$$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$$其中实例$x_i$属于输入空间，$x_i\in \mathcal{X}={\mathbf{R}}^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots ,N$，$y_i$为$x_i$的类标记，如果能用$R^n$中的一个超曲面将正负实例正确分开，则称这个问题为非线性可分问题。

非线性分类问题的求解思路：进行一个非线性变换，将非线性问题变换为线性问题，通过解变换后的线性问题求解原来的非线性问题.对于上图中的例子，通过变换，将左图中椭圆变换成右图中的直线，将非线性分类问题变换为线性分类问题。
符号推导如下：
设原空间为$\mathcal{X}\subset {\mathbf{R}}^2,x={\left(x^{(1)},x^{(2)}\right)}^{\mathrm{T}}\in \mathcal{X}$，新空间为$\mathcal{Z}\subset {\mathbf{R}}^2,z={\left(z^{(1)},z^{(2)}\right)}^T\in \mathcal{Z}$，定义从原空间到新空间的变换(映射):$$z=\varphi (x)={\left({\left(x^{(1)}\right)}^2,{\left(x^{(2)}\right)}^2\right)}^{\mathrm{T}}$$
经过变换$z=\varphi (x)$，原空间$\mathcal{X}\subset {\mathbf{R}}^2$变换为新空间$\mathcal{Z}\subset {\mathbf{R}}^2$，原空间中的点相应地变换为新空间中的点，原空间中的椭圆
$$w_1{\left(x^{(1)}\right)}^2+w_2{\left(x^{(2)}\right)}^2+b=0$$
变换为新空间中的直线$$w_1{z}^{(1)}+w_2{z}^{(2)}+b=0$$在变换后的新空间中，直线$w_1{z}^{(1)}+w_2{z}^{(2)}+b=0$可以将变换后的正负实例点正确分开.这样，原空间中的非线性可分问题就变成了新空间中的线性可分问题.

2.核函数的定义

定义6(核函数) 设$\mathcal{X}$是输入空间(欧氏空间$R^n$的子集或离散集合)，又设$\mathcal{H}$为特征空间(希尔伯特空间)，如果存在一个$\mathcal{X}$到$\mathcal{H}$的映射$$\varphi (x):\mathcal{X}\to \mathcal{H}$$使得对所有$x,z\in \mathcal{X}$，函数$K(x,z)$满足条件
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$则称$K(x,z)$为核函数，$\varphi (x)$为映射函数，式中$\varphi (x)\cdot \varphi (z)$为和$\varphi (z)$的内积。
以下为本节的最重要技术核技巧，核技巧巧妙地利用线性分类学习方法与核函数解决非线性问题的技术.
核技巧的思路：在学习和预测中只定义核函数$K(x,z)$，而不显式地定义映射函数$\varphi (x)$.通常，直接计算$K(x,z)$比较容易，而通过$\varphi (x)$和$\varphi (z)$计算$K(x,z)$并不容易.注意，$\varphi (x)$是输入空间$R^n$到特征空间$\mathcal{H}$的映射，特征空间$\mathcal{H}$一般是高维的，甚至是无穷维的.可以看到，对于给定的核$K(x,z)$，特征空间$\mathcal{H}$和映射函数$\varphi (x)$的取法并不唯一，可以取不同的特征空间，即便是在同一特征空间里也可以取不同的映射.
下例说明核函数和映射函数的关系.
假设输入空间是$R^2$,核函数是$K(x,z)=(x\cdot z{)}^2$，试找出其相关的特征空间$\mathcal{H}$和映射$\varphi (x):{\mathbf{R}}^2\to \mathcal{H}$.
解 取特征空间$\mathcal{H}={\mathbf{R}}^3$，记$x={\left(x^{(1)},x^{(2)}\right)}^{\mathrm{T}},z={\left(z^{(1)},z^{(2)}\right)}^{\mathrm{T}}$，由于$$(x\cdot z{)}^2={\left(x^{(1)}{z}^{(1)}+x^{(2)}{z}^{(2)}\right)}^2={\left(x^{(1)}{z}^{(1)}\right)}^2+2x^{(1)}{z}^{(1)}{x}^{(2)}{z}^{(2)}+{\left(x^{(2)}{z}^{(2)}\right)}^2$$
所以可以取映射$$\varphi (x)={\left({\left(x^{(1)}\right)}^2,\sqrt{2}{x}^{(1)}{x}^{(2)},{\left(x^{(2)}\right)}^2\right)}^{\mathrm{T}}$$容易验证$\varphi (x)\cdot \varphi (z)=(x\cdot z{)}^2=K(x,z)$
仍取$\mathcal{H}={\mathbf{R}}^3$以及$$\varphi (x)=\frac{1}{\sqrt{2}}{\left({\left(x^{(1)}\right)}^2-{\left(x^{(2)}\right)}^2,2x^{(1)}{x}^{(2)},{\left(x^{(1)}\right)}^2+{\left(x^{(2)}\right)}^2\right)}^{\mathrm{T}}$$同样有$\varphi (x)\cdot \varphi (z)=(x\cdot z{)}^2=K(x,z)$
还可以取$\mathcal{H}={\mathbf{R}}^4$和$\varphi (x)={\left({\left(x^{(1)}\right)}^2,x^{(1)}{x}^{(2)},x^{(1)}{x}^{(2)},{\left(x^{(2)}\right)}^2\right)}^{\mathrm{T}}$

3.核技巧在支持向量机中的应用

注意到在线性支持向量机的对偶问题中，目标函数和决策函数都只涉及输入实例和实例之间的内积$x_i\cdot x_j$。在对偶问题的目标函数中的内积可以用核函数$K\left(x_i,x_j\right)=\varphi \left(x_i\right)\cdot \varphi \left(x_j\right)$来代替，此时对偶问题的目标函数成为$$W(\alpha )=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)-\sum _{i=1}^N{\alpha }_i$$同样，分类决策函数中的内积也可以用核函数代替，而分类决策函数为
$$f(x)=\mathrm{sign}\left(\sum _{i=1}^{N_s}{a}_i^{\ast }{y}_i\varphi \left(x_i\right)\cdot \varphi (x)+b^{\ast }\right)=\mathrm{sign}\left(\sum _{i=1}^{N_s}{a}_i^{\ast }{y}_{i}K\left(x_i,x\right)+b^{\ast }\right)$$等价于经过映射将原来的输入空间变换到一个新的特征空间，将输入空间中的内积变换为特征空间的内积在新的特征空间里从训练样本中学习线性支持向量机。当映射函数是非线性函数时，学习到的含有核函数的支持向量机是非线性分类模型.学习是隐式地在特征空间进行的，不需要显示地定义特征空间和映射函数.这样的技巧称为核技巧。在实际应用中，往往依赖领域知识直接选择核函数，核函数选择的有效性需要通过实验验证。

4.正定核

核心问题：函数$K(x,z)$满足什么条件才能称为核函数？
已知映射函数$\varphi (x)$，通过$\varphi (x)$和$\varphi (z)$的内积求得核函数$K(x,z)$，不用构造映射$\varphi (x)$能否直接判断一个给定的函数$K(x,z)$是不是核函数？
假设$K(x,z)$是定义在上的对称函数，并且对任意的$x_1,x_2,\cdots ,x_m\in \mathcal{X}$，$K(x,z)$关于$x_1,x_2,\cdots ,x_m\in \mathcal{X}$的Gram矩阵是半正定的.可以依据函数$K(x,z)$，构成一个希尔伯特空间(Hilbert space)，其步骤是：首先定义映射$\varphi (x)$并构成向量空间$S$；然后在$S$上定义内积构成内积空间；最后将$S$完备化构成希尔伯特空间。

定理5(正定核的充要条件) 设$K:\mathcal{X}\times \mathcal{X}\to \mathbf{R}$是对称函数，则$K(x,z)$为正定核函数的充要条件是对任意$x_i\in \mathcal{X},i=1,2,\cdots ,m$，$K(x,z)$对应的Gram矩阵：
$$K={\left[K\left(x_i,x_j\right)\right]}_{m\times m}$$是半正定矩阵。
定理给出了正定核的充要条件，因此可以作为正定核，即核函数的另一定义.

定义7(正定核的等价定义) 设$\mathcal{X}\subset {\mathbf{R}}^n$，$K(x,z)$是定义在$\mathcal{X}\times \mathcal{X}$上的对称函数，如果对任意的$x_i\in \mathcal{X},i=1,2,\cdots ,m$，对应的Gram矩阵：$$K={\left[K\left(x_i,x_j\right)\right]}_{m\times m}$$是半正定矩阵，则称是正定核。

5.常用核函数

1).多项式核函数$$K(x,z)=(x\cdot z+1{)}^p$$对应的支持向量机是一个多项式分类器，在此情形下，分类决策函数成为

2).高斯核函数$$K(x,z)=\exp \left(-\frac{\Vert x-z{\Vert }^2}{2{\sigma }^2}\right)$$对应的支持向量机是高斯径向基函数(radical basis function)分类器，在此情况下，分类决策函数成为
$$f(x)=\mathrm{sign}\left(\sum _{i=1}^{N_s}{a}_i^{\ast }{y}_i\exp \left(-\frac{\Vert x-z{\Vert }^2}{2{\sigma }^2}\right)+b^{\ast }\right)$$
3).字符串核函数(string kernel function)
核函数不仅可以定义在欧氏空间上，还可以定义在离散数据的集合上.比如，字符串核是定义在字符串集合上的核函数，字符串核函数在文本分类、信息检索、生物信息学等方面都有应用
考虑一个有限字符表$\Sigma$.字符串$s$是从$\Sigma$中提取的有限个字符的序列，包括空字符串，字符串$s$的长度用$|s|$表示，它的元素记作$s(1)s(2)\cdots s(|s|)$.两个字符串$s$和$t$的连接记作$st$，所有长度为$n$的字符串的集合记作${\Sigma }^n$，所有字符串的集合记作${\Sigma }^{\ast }={\bigcup }_{n=0}^{\infty }{\Sigma }^n$
考虑字符串$s$的子串$u$.给定一个指标$i=\left(i_1,i_2,\cdots ,i_{|u|}\right)$ ,$s$的子串$u$定义为$u=s(i)=s\left(i_1\right)s\left(i_2\right)\cdots s\left(i_{|u|}\right)$，其长度记作$l(i)=i_{|u|}-i_1+1$,如果是连续的(没有空格)，则$l(i)=|u|$；否则，$l(i)>|u|$.
假设$S$是长度大于或等于$n$字符串的集合，$s$是$S$的元素。现在要建立字符串集合$S$到特征空间${\mathcal{H}}_n=R^{{\Sigma }^n}$的映射${\varphi }_n(s)$。$R^{{\Sigma }^n}$表示定义在上的实数空间，其每一维对应一个字符串$u\in {\Sigma }^n$，映射${\varphi }_n(s)$
将字符串$s$对应于空间$R^{{\Sigma }^n}$的一个向量，其在$u$维上的取值为
$${\left[{\varphi }_n(s)\right]}_u=\sum _{i:s(i)=u}{\lambda }^{l(i)}$$这里，$0<\lambda ⩽1$是一个衰减函数，$l(i)$表示字符串的长度，求和在$s$中所有于$u$相同的子串上进行.
例如，假设$\Sigma$为英文字符集，$n$为3，为长度大于或等于3的子串集合.考虑将字符集$S$映射到特征空间$H_3$，$H_3$的一维对应于字符串$asd$，这时字符串$\text{ "Nasdaq" }$与$\text{ "lass das" }$在这一维上的值分别是
${\left[{\varphi }_3(\text{ Nasdaq })\right]}_{asd}={\lambda }^3$和${\left[{\varphi }_3(\text{ lass das }]\right]}_{ad}=2{\lambda }^5$.在第1个字符串中，$asd$是连续的字符串，在第2个字符串中，$asd$是长度为5的不连续子串，共出现2次。
两个字符串$s$和$t$上的字符串核函数是基于映射${\varphi }_n$的特征空间的内积：
$$k_n(s,t)=\sum _{u\in {\Sigma }^n}{\left[{\varphi }_n(s)\right]}_u{\left[{\varphi }_n(t)\right]}_u=\sum _{u\in {\Sigma }^n}\sum _{(i,j)s(i)=t(j)=u}{\lambda }^{l(i)}{\lambda }^{l(j)}$$字符串核函数$k_n(s,t)$给出了字符串$s$和$t$中长度等于$n$的所有子串组成的特征向量的余弦相似度，直观上，两个字符串相同的子串越多，它们就越相似，字符串核函数的值越大，字符串核函数可以由动态规划快速地计算.

6.非线性支持向量机学习算法

(1).选取适当的核函数$K(x,z)$(正定核函数)和适当的参数$C$，构造并求解最优化问题$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)-\sum _{i=1}^N{\alpha }_i$$$$\text{ s.t. }\sum _{i=1}^N{\alpha }_i{y}_i=0$$$$0⩽{\alpha }_i⩽C,i=1,2,\cdots ,N$$求得最优解${\alpha }^{\ast }={\left({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }\right)}^{\mathrm{T}}$
(2).选择${\alpha }^{\ast }$的一个正分量$0<{\alpha }_j^{\ast }<C$，计算$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K\left(x_i\cdot x_j\right)$$(3).构造决策函数
$$f(x)=\mathrm{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K\left(x\cdot x_i\right)+b^{\ast }\right)$$

参考： 李航《统计学习方法》