数据结构 - Java -韩顺平 图解Java数据结构和算法
数据结构 Lesson 1
- 数据结构的知识总结
- 1. 几个经典的算法面试题
- 2. 线性结构与非线性结构
- 2.1 稀疏数组 sparsearray
- 2.2 队列
- 2.2.1 顺序队列:
- 2.2.2 环形队列(取模 %)
- 2.3 链表(linked list)
- 2.3.1. 单向链表
- 2.3.2 双向链表
- 2.3.3 环形链表
- 2.4 栈 (Stack)
- 2.4.1 利用数组模拟栈:
- 2.4.2 用栈来实现综合计算器:
- 2.4.3 前缀、中缀、后缀(逆波兰)表达式
- 3. 递归 Recursion
- 3.1 打印问题
- 3.2 阶乘问题
- 3.3 八皇后问题
- 4.排序算法 Sort Algorithm
- 4.1 冒泡排序 Bubble Sort
- 4.2 选择排序 Select Sort
- 4.3 插入排序 Insert Sort
- 4.4 希尔排序 Shell Sort
- 4.4 快速排序 Quick Sort
- 4.5 归并排序 Merge Sort
- 4.5 基数排序 Radix Sort
- 5 查找算法
- 5.1 线性查找
- 5.2 二分查找
- 5.3 插值查找
- 5.4 斐波那契查找(黄金分割查找):
- 6.哈希表(数组+链表)
- 7.树结构
- 7.1 顺序存储二叉树
- 7.2 线索化二叉树
- 7.3 堆排序
- 7.3 赫夫曼树
- 7.4 赫夫曼编码
- 7.5 二叉排序树(Binary Sort Tree)
- 7.6 平衡二叉树(AVL树)
- 7.7 多路查找树
- 8 图
数据结构的知识总结
看完了Java -韩顺平 图解Java数据结构和算法,虽然课程已经提供了较为完整的讲义,但是自己仍旧需要对所学习的知识进行一个总结,也是对课程进行一个整体的回顾。
1. 几个经典的算法面试题
Ø KMP算法, 建立《部分匹配表》 【字符串匹配问题】
Ø 汉诺塔游戏 分治算法 【三个为一组开始动肯定可以完成,最笨的方法】
Ø 八皇后问题 【棋盘上放置象棋的问题】分治算法
Ø 马踏棋盘问题 深度优化遍历算法(DFS)+贪心算法优化【棋盘上放马走日要全部走完的问题】
Ø 字符串替换问题 => 单链表数据结构
Ø 五子棋问题 二维数组 => 稀疏数组
Ø 丢手帕问题 约瑟夫问题 => 单向环形链表
Ø 修路问题 =>最小生成树(加权值)+ 普利姆算法
Ø 最短路径问题 => 图+弗洛伊德算法
Ø 汉诺塔游戏 分支算法
Ø八皇后问题 => 回溯算法
2. 线性结构与非线性结构
线性结构:是一个有序数据元素的集合
1. 数据元素之间存在一对一关系 a[1] = 0
2. 顺序存储结构(地址连续,顺序表),链式存储结构(地址不一定连续,链表)
3. 数组,队列,链表,栈
非线性结构
二维数组,多维数组,广义表,树结构,图结构
2.1 稀疏数组 sparsearray
当一个数组中大部分元素为0,或者为同一值的数组时,可以使用稀疏数组来保存该数组。
1. 记录数组一共有几行几列,有多少个不同的值 (说是一共有多少个?或者说应该是有意义的值)
2. 把不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
将稀疏数组转成原始的二维数组的思路
1. 先读取稀疏数组的第一行,创建原始的二维数组。
2. 再读取稀疏数组的后几行数据,并赋值给原始的二维数组。
2.2 队列
有序列表,可以用数组或者链表实现【 先入先出/排队】
2.2.1 顺序队列:
1) front = -1; rear = -1. 个数:rear - front
2) front 指向队列头部,指向队列头的前一个位置(0=>-1 ; 1=>0)
3) rear 指向队列尾部,并指向队列尾的数据.
**模拟队列**:加入后,尾指针往后移, rear+1.但是当rear=maxSzie-1,不能再加入。(已经满了)
**缺点**:目前的数组只能使用一次。删除以后占据了位置,不能再加入新的数据。“假溢出”
2.2.2 环形队列(取模 %)
1) front 调整:front 指向队列的第一个元素。 front=0
2) rear调整:rear指向队列最后一个元素的后一个位置,(空闲单元法 )rear = 0
3) 满:(rear+1)%maxsize = front 【多留了一个空间】
4) 空:rear = front
**有效数据的个数**(rear+maxsize-front)%maxsize [加maxsize是有时会 rear < front]
2.3 链表(linked list)
2.3.1. 单向链表
1) 链表是以节点的方式存储
2) 每个节点包括data域和next域
3) 各个节点不一定是连续存储
4) 分有带头节点的链表和没有头节点的链表(根据需求确定)
单向链表的增删改查
1) 添加(直接加到最后)先创建一个head,再添加节点,直接加入到最后,通过一个辅助变量遍历,从而遍历整个链表。
2) 添加(顺序)找到新添加节点的位置,辅助节点temp为新节点的前一个,新节点的.next = temp.next.然后temp.next = 新节点
3) 修改,找对应的节点,然后修改数据
4) 删除,找到需要删除的节点,前一个辅助节点temp.next = temp.next.next. [被删除的节点会被垃圾回收机制回收]
5) 查找,利用**while(true){ }**查找,返回即可
有效节点个数:直接while循环即可
获取倒数第K个节点:先找出长度,再遍历。 size-index(从第一个有效节点开始遍历,注意:i=0)
HeroNode cur = head.next;
for (int i = 0; i < size-index; i++) {
cur = cur.next;
}
**反转:**先创建一个新的reverseHead,然后cur.next = reverse.next; reverse.next = cur;
(首先保证指向顺序变,再保证插入到新的头结点后);
HeroNode cur = head.next;
HeroNode next = null;
HeroNode reverseHead = new HeroNode(0,"","");
while (cur!=null){
next = cur.next;
cur.next = reverseHead.next;//修改节点的指向顺序
reverseHead.next = cur;//修改,将cur插入到头后边
cur = next;
}
head.next = reverseHead.next;
反转打印可以利用Stack栈的push、pop。
2.3.2 双向链表
每个节点具有data,next和pre的域,变成了可以向前也可以向后遍历的链表
双向链表的增删改查
1) 添加,直接添加到最后。遍历找到最后,然后添加。
temp.next = newHeroNode;newHeroNode.pre = temp
如果是按照顺序添加,需要找到前一个temp,判断是不是最后一个(或者是头),然后添加。
if (temp.next!=null){
temp.next.pre = heroNode;
}
heroNode.next = temp.next;
heroNode.pre = temp;
temp.next = heroNode;
2) 修改,和单向链表一样
3) 删除,直接找到这个节点temp(可以自我删除)
temp.pre.next = temp.next; temp.next.pre = temp.pre
(注意判断是不是最后一个节点,if(temp.next!=null)才有后边那个)
4) 查找,遍历即可
2.3.3 环形链表
单向环形链表
约瑟夫(Josephu) 问题:单向环形链表,出队列
构建单向环形链表:
1)创建第一个节点first,自成环
2)创建新节点加入已有的环形链表中。
3) 辅助指针curBoy,指向first;每加入一个新的节点,curBoy进行移动;
通过while循环增加新节点;最后curBoy.next = first结束
出队列:
1)先从first开始,创建helper指针(位于first的前一个)
2)再移动first到实际要从哪个指针开始的位置,也要移动helper
(要从自身开始计数,所以是移动了第m-1次)
3)然后for循环,first和helper都移动,最后到指定位置后将节点去除
(first = first.next ; helper.next = first)
2.4 栈 (Stack)
先入后出 ( FILO==>first in last out ) 的有序列表;
栈顶(允许删除和插入 Top)和栈底(固定 Bottom);
入栈(push)和出栈(pop);
2.4.1 利用数组模拟栈:
栈顶top;
入栈:top++;stack[top] = data;
出栈: value = stack[top];top--;return value;
2.4.2 用栈来实现综合计算器:
1) 使用index索引,来遍历,通过判断是数字还是操作符,分别加入到不同的栈中
2) 数字=>直接入栈;[遍历时,要注意拼接,不能只算一个]
操作符=>①符号栈为空,则直接入栈;②符号栈已有操作符,那么如果当前的操作符优先级小于或者
等于栈中的操作符,就从数栈中pop两个数,符号栈中pop出一个符号,进行运算,将结果入数栈,
新的操作符入符号栈;如果当前的操作符优先级大于栈中的操作符,就直接入栈。【int和char可以混用】
3) 当表达式扫描完毕,就顺序从数栈和符号栈中pop出相应的数和符号,并运行计算。
4) 当数栈最后只有一个数字,就是表达式的结果。
2.4.3 前缀、中缀、后缀(逆波兰)表达式
前缀:
从右至左扫描表达式,数字==>入栈;运算符==>弹出栈顶的两个数,计算后入栈;重复至表达式最左端,
最后得到的值为结果。(3+4)*5-6 ==> - * + 3 4 5 6
中缀:
就是人们普遍熟悉的,计算机不好操作,因此要转为后缀表达式,再计算。
后缀:
从左至右扫描表达式,数字==>入栈;运算符==>弹出栈顶的两个数,计算后入栈;重复至表达式最右端,
最后得到的值为结果。(3+4)*5-6 ==> 3 4 + 5 * 6 - (与前缀的顺序不同)
中缀==>后缀==>计算:
1. 初始化两个栈:符号栈s1和储存中间结果的栈s2(s2可以使用ArrayList,这样就不用在反序)。
2. 从左到右扫描,操作数==>加入s2; 运算符==> ①s1为空或者栈顶为"(",直接入栈。②若此时的符号优先级比s1栈顶的优先级高,则入栈。③ 若比栈顶的优先级低或者一样,将栈顶的peek()加入s2,再继续比较。
while (s1.size()!=0 && Operation.getValue(s1.peek())>= Operation.getValue(item)){
s2.add(s1.pop());
}
s1.push(item);
3. 遇到括号:如果是"("==>加入s1;如果是")"==>依次弹出s1栈顶的运算符,加入s2,直到遇到左括号,并将左括号丢弃。
else if (item.equals("(")) {
s1.add(item);
} else if (item.equals(")")) {
//如果是右括号,要将符号栈的移动到数栈,直到左括号(最后要删除)
while (!s1.peek().equals("(")) {
s2.add(s1.pop());
}
s1.pop();
4. 重复至表达式最右,最后将s1中的运算符加入s2。
5. 依次弹出s2的元素,再逆序就是对应的后缀表达式。(如果是ArrayList, 不用再逆序了)
3. 递归 Recursion
迷宫问题(回溯),递归(Recursion);就是自己调用自己
3.1 打印问题
test(4)==>
test(3)==>
test(2)==>sout(进行输出)
==> test(3)[实际没有了输出,不满足else;若没有else,可以进行输出]
==> test(4) 同上
==> 输出n=2
3.2 阶乘问题
3.3 八皇后问题
ctrl + alt + v 快速生成对象
判断是否冲突:
private boolean judge(int n){
for (int i = 0; i < n; i++) {
// 因为arr[i] = val; val表示第i+1个皇后,放在第i+1行,第val+1列
if (array[n]==array[i]||Math.abs(n-i)==Math.abs(array[i]-array[n])){
return false;
}
}
return true;
}
private void check(int n){
if (n==max){
print();
return;
}
for (int i = 0; i < max; i++) {
// i 表示从第一列
array[n]=i;//n从0开始,进行回溯,n+1;每一行都是从第一列i=0开始的
if (judge(n)){
//判断是不是冲突,就是判断在第n+1个位置的值与其他值是不是冲突
check(n+1);
}
}
}
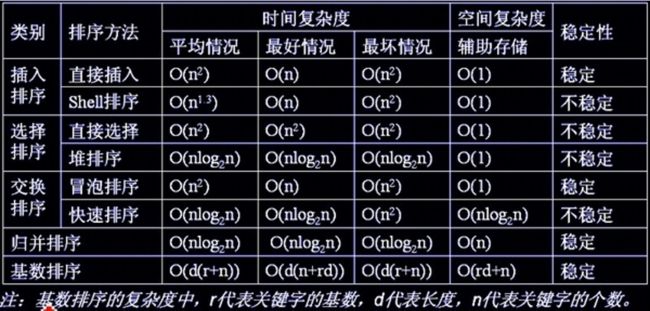
4.排序算法 Sort Algorithm
排序是将一组数据,依指定的顺序进行排列的过程。
排序分类:内部排序(将数据加载到内存中进行排序)和外部排序(数据量过大,外部存储)

度量执行时间的方法:事后统计(运行程序得到结果,要保证条件一致)和事前估算(分析算法的时间复杂度)
时间(语句)频度:T(n) 一个算法中语句执行次数

常见的时间复杂度:
| 常数阶 | 对数阶 | 线性阶 | 线性对数阶 | 平方阶 | 立方阶 | k次方阶 | 指数阶 |
|---|---|---|---|---|---|---|---|
| O(1) | O(log2n) | O(n) | O(nlog2n) | O(n^2) | O(n3) | O(nk) | O(2n) |
4.1 冒泡排序 Bubble Sort
从头开始找,进行了n-1次遍历,复杂。可以判断有序后提前终止,优化;
public static void bubblesort1(int arr[]){
int temp=0;
boolean flag = false;
for (int i = 0; i <arr.length-1; i++) {
for (int j = 0; j <arr.length-1-i; j++) {
if (arr[j]>arr[j+1]){
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
flag=true;
}
}
if(!flag){
break;
}else {
flag=false;
}
}
}
关于时间的一段代码:
Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String dateStr1 = simpleDateFormat.format(date1);
System.out.println(dateStr1);
4.2 选择排序 Select Sort
依次选择最小的,与最前边的交换顺序。进行n-1次。(比冒泡排序时间缩短)
{3,5,6,1,2}=>{1,5,6,3,2}=>{1,2,6,3,5}=>{1,2,3,6,5}=>{1,2,3,5,6}
public static void selectsort1(int[] arr) {
for (int i = 0; i < arr.length-1; i++) {
int minIndex = i;
int min = arr[i];
for (int j = i+1 ; j < arr.length; j++) {
if (min>arr[j]){
min=arr[j];
minIndex=j;
}
}
if (minIndex!=i){
arr[minIndex]=arr[i];
arr[i] = min;
}
}
}
4.3 插入排序 Insert Sort
有序表和无序表,n-1次
以第一个为有序表,从无序表第二个开始,进行比较,并加入到合适的位置。
缺点:加入的过程中,比较时,如果不满足条件,就会一直将数移动(进行了一个复制);假如数值过大或过小(与排序的规则有关),那么移动的次数就较多,对效率有影响。
public static void insertSort1(int[] arr){
for (int i = 1; i < arr.length; i++) {
int insertIndex = i-1;
int insertVal = arr[i];
// 从第2个数开始,第一个数已经是规定为有序的,通过判断,来改变整个队列;
// 开始的这个数和他前边的一个比较,如果小再比较前边的,不小就放到后边。
while (insertIndex>=0&&insertVal<arr[insertIndex]){
//这个数比比较的数小,那么久把比较的数后移一个,并把下标指向前一个数。
// 这样中间的就可以算是一个空(实际上是有值的),通过判断来填补。
arr[insertIndex+1] = arr[insertIndex];
insertIndex--;
}
//insertIndex此时应该指向的是需要比较的数的下标,不满足比它小,所以放在后边要加一,
if (insertIndex+1!=i){
arr[insertIndex+1] = insertVal;
}
}
}
4.4 希尔排序 Shell Sort
把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分为一组,算法终止。再进行一定的调整就可以了。
先分组,再直接排序。(又分为交换法和移动法)
//交换法,效率低,发现就交换;
public static void shellsort1(int[] arr){
int temp=0;
int count = 0;
for (int gap = arr.length/2; gap>0; gap=gap/2) {
// 希尔排序的分组
for (int i = gap; i <arr.length; i++) {
for (int j = i-gap; j>=0; j=j-gap) {
//是进行了交换。分组后,从分组的第二个开始,与前一个比较,
// 如果不符合条件,就更改顺序;最后遍历了整个分组,
// 到最后,得到两两比较的结果
if (arr[j]>arr[j+gap]){
temp=arr[j];
arr[j] = arr[j+gap];
arr[j+gap] = temp;
}
}
}
System.out.println("第几轮"+(++count)+ Arrays.toString(arr));
}
}
**这个要多理解理解!!!**
/移动法,速度较快
public static void shellSort2(int[] arr){
//增量gap,逐步缩小增量
for (int gap = arr.length/2; gap >0; gap=gap/2) {
//从第gap个元素,逐步对其所在的组进行直接插入
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp=arr[i];
if (arr[j]<arr[j-gap]){
while (j-gap>=0&&temp<arr[j-gap]){
arr[j] = arr[j-gap];
j-=gap;
}
// j-gap此时是小的
//当退出while后,就找到了temp的位置
arr[j]=temp;
}
}
}
}
4.4 快速排序 Quick Sort
对冒泡排序的一种改进,通过将要排序的数据分割成独立的两部分,其中一部分所有数据比另一部分所有数据都要小,然后再对这两个部分进行快速排序。整个排序过程可以递归进行。
public static void quciksort1(int[] arr, int left, int right){
int l=left;
int r=right;
int midVal = arr[(left+right)/2];
int temp=0;
// System.out.println(l+" "+Arrays.toString(arr)+" "+ r);
//循环,让比小的去一边,比大的去另一边
while (l<r){
//找到比他小的值,比中间值大就会退出while(没有考虑相等,最后要考虑)
while (arr[l]<midVal){
l++;
}
//找到右边比中间值大的值,比中间值小就会退出while
while (arr[r]>midVal){
r--;
}
if (l>=r){
//表示,此时左右两边都遍历完了,可以退出循环了
break;
}
temp= arr[l];
arr[l]=arr[r];
arr[r]=temp;
//如果交换完后,发现左边有值等于中间值,可能会造成进不去循环了,要自己移动
if (arr[l]==midVal){
r--;
}
if (arr[r]==midVal){
l++;
}
}
System.out.println(Arrays.toString(arr));
System.out.println(r+" "+l);
if (l==r){
l++;
r--;
}
System.out.println(r+" "+l);
//这一步是,对以后得到的进行循环
if (left<r){
quciksort1(arr,left,r);
}
if (right>l){
quciksort1(arr,l,right);
}
}
4.5 归并排序 Merge Sort
分+治(divide-and- conquer);采用经典的分治策略;将问题分解成小的问题然后递归求解,治是将分的阶段得到的答案修补在一起。
//分+和
public static void separate(int[] arr,int left,int right,int[] temp){
if (left<right){
int mid = (left+right)/2;
//左
separate(arr,left,mid,temp);
//右
separate(arr,mid+1,right,temp);
//合
merge(arr,left,mid,right,temp);
}
}
//和
public static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;
int j = mid+1;
int t=0;
//比较,然后添加到temp,有一边到头就退出循环,然后再把剩下没有比的加到temp最后
while (i<=mid&&j<=right){
if (arr[i]<=arr[j]){
temp[t] = arr[i];
t+=1;
i+=1;
}else {
temp[t]=arr[j];
t+=1;
j+=1;
}
}
//把剩下的加进去
while (i<=mid){
temp[t]=arr[i];
i+=1;
t+=1;
}
while (j<=right){
temp[t]=arr[j];
j+=1;
t+=1;
}
//把temp的复制到arr
t=0;
int templeft=left;
//表示的是arr的索引,如果是0的话,每进入一次方法,就会覆盖
while (templeft<=right){
arr[templeft]=temp[t];
t+=1;
templeft+=1;
}
}
4.5 基数排序 Radix Sort
属于分配式排序distribution sort,桶子法bucket/bin sort;通过键值的各个位的值,将要排序的元素分配至某些桶中,达到排序的作用。是稳定性排序;
就是从个位开始,遍历数组,放置到桶中,再按顺序取出;再找十位,直到找到最高位的。
int forCount = (max+"").length();
for (int j = 0; j < forCount; j++) {
int n= (int) Math.pow(10,j);
// int n= 10^j;不能使用这种,这是关系运算符,按位异或运算符
// System.out.println(n);
int[][] bucket = new int[10][arr.length];
//每个桶的个数,要统计一下,方便取出
int[] bucketCount = new int[10];
for (int k = 0; k < arr.length ; k++) {
int reaminder = arr[k]/n%10;
bucket[reaminder][bucketCount[reaminder]] = arr[k];
bucketCount[reaminder]++;
}
//按照这个顺序,取出来
int index=0;
for (int i = 0; i < bucket.length; i++) {
if (bucketCount[i]!=0){
for (int k = 0; k < bucketCount[i]; k++) {
arr[index]=bucket[i][k];
index++;
}
}
bucketCount[i]=0;
}
System.out.println("处理"+(j+1)+"次"+ Arrays.toString(arr));
}
5 查找算法
5.1 线性查找
从开始一个一个遍历进行查找
5.2 二分查找
有序数组,mid=(left+right)/2;通过比较,二分递归,从左或右进行查找。
(可以通过递归,也可以不通过递归)
public static ArrayList<Integer> binarySearch2(int[] arr, int left, int right, int findVal){
int mid = (left+right)/2;
int midVal = arr[mid];
if (left>right){
return new ArrayList<Integer>();
}
if (findVal>midVal){
//向右递归
return binarySearch2(arr,mid+1,right,findVal);
}else if (findVal<midVal){
return binarySearch2(arr,left,mid-1,findVal);
}else {
ArrayList<Integer> resIndexList = new ArrayList<>();
int temp = mid-1;
//左
while (true){
if (temp<0 || arr[temp]!=findVal){
break;
}
resIndexList.add(temp);
temp--;
}
//中
resIndexList.add(mid);
//右
temp = mid+1;
while (true){
if (temp>arr.length-1 || arr[temp]!=findVal){
break;
}
resIndexList.add(temp);
temp++;
}
return resIndexList;
}
}
可以通过递归也可以通过循环得到
/**
* 这里找到的只有一个,并么有考虑重复值
* @param arr
* @param left 索引是为递归做准备
* @param right
* @param findVal
* @return
*/
public static int binarySearch(int[] arr, int left, int right, int findVal){
int mid = (left+right)/2;
int midVal = arr[mid];
if (left>right){
return -1;
}
if (findVal>midVal){
//向右递归
return binarySearch(arr,mid+1,right,findVal);
}else if (findVal<midVal){
return binarySearch(arr,left,mid-1,findVal);
}else {
return mid;
}
}
/**
* 二分查找的非递归实现
* @param arr 假设是升序排列 ,未考虑重复的情况
* @param targetVal
* @return
*/
public static int binarySearch(int[] arr,int targetVal){
int left=0;
int right = arr.length-1;
while (left<=right){
int mid = (left+right)/2;
if (targetVal==arr[mid]){
return mid;
}else if (arr[mid]>targetVal){
right=mid-1;
}else {
left=mid+1;
}
}
return -1;
}
5.3 插值查找
类似二分
int mid = left+ (right-left)*(findVal-arr[left])/(arr[right]-arr[left]);
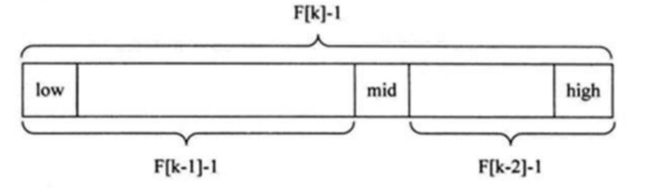
5.4 斐波那契查找(黄金分割查找):
| F[k]=F[k-1]+F[k-2]==>F[k]-1=(F[k-1]-1)+(F[k-2]-1)+1 |
|---|
只要顺序表长度为F[k]-1;可以将该表长度分为F[k-1]-1和F[k-2]-1两端,然后剩下了中间值。mid=low+F[k-1]-1然后每一个子段都可以用相同方式分割。
注意:顺序表n长度不一定是F[k]-1;不够的话就补全(就是复制最后的数,使得总的长度为F[k]-1)
public static int fibSearch(int[] a,int key){
int low = 0;
int high = a.length-1;
int k = 0;//表示斐波那契数列的下标,当然是根据k==>k-1==>k-2 变化的
int mid = 0;
int f[] = fib();
//获取斐波那契的k
while (high>f[k]-1){
k++;
}
//因为f(k)的值[f(k)是需要的长度,0==>f(k)-1]可能会大于a的长度[始终是大于或者等于,不可小于,小于就再让k增加],
// 所以需使用Arrays类,创造一个新的数组,并指向a【】
int[] temp = Arrays.copyOf(a,f[k]); //就是假如a
//此外,还需要使用a数组的最后数填充a.length到f(k)-1下标的值,
for (int i = high+1; i < temp.length; i++) {
temp[i] = a[high];
}
//while 循环处理,找到key
while (low<=high){
mid = low + f[k-1]-1;
if (key<temp[mid]){
high=mid-1;
k--;
}else if (key>temp[mid]){
low = mid +1;
k= k-2;
}else {
if (mid<=high){
return mid;
}else {
return high;
}
}
}
return -1;
}
6.哈希表(数组+链表)
是根据关键码值而直接访问的数据结构。通过关键码值映射到表中的一个位置来访问记录,以加快寻找的速度。
映射函数也可以叫散列函数。存放记录的数据叫作散列表。
emp==>链表==>数组(千万别忘记初始化)
7.树结构
数组:方便查找,但是不方便加入或者删除;
链表:方便加入或者删除,但是查找效率太低。
树:能提高存储和读取的效率;既可以保证检索速度,也可以保证数据的插入,删除,修改速度。
满二叉树:所有叶子节点在最后一层,并且节点总数为2^n-1.
完全二叉树:在最后一层或者倒数第二层;最后一层左连续,倒数第二层右连续。
前中后序遍历:和父节点的输出顺序有关。
| 前:父=>左=>右 | 中:左=>中=>右 后: | 左=>右=>父 |
|---|
类似的有前中后序查找,注意判断的位置即可;
if (this.no==no){
return this;
}
删除的话,判断this.next是不是,然后置空。要进行左遍历和右遍历。
7.1 顺序存储二叉树
通常只考虑完全二叉树;(可以进行前中后序的读取)
第n个元素的左子节点为2*n+1;右为2*n+2;第n个元素的父节点为(n-1)/2;
n表示二叉树的第几个元素,从0开始编号的。
7.2 线索化二叉树
前驱节点和后继节点
在node中加入了
leftType; //为0,表示指向左子树,为1表示前驱节点
rightType ; //0==>右子树;1==>后继节点
private HeroNode root;
// 为了实现线索化,需要创建要给指向当前节点的前驱节点的指针;
// 始终是要有前驱节点的
private HeroNode pre;
public void setRoot(HeroNode root) {
this.root = root;
}
public void threadedNodes(){
this.threadedNodes(root);
}
//遍历
public void threadedList(){
//定义一个变量,存储当前遍历的节点,从root开始
HeroNode node = root;
while (node!=null){
//后面随着遍历而变化,因为leftType==1时,该节点是线索化的,
while (node.getLeftType()==0){
node = node.getLeft();
}
System.out.println(node);
while (node.getRightType()==1){
node = node.getRight();
System.out.println(node);
}
//替换这个遍历的节点
node = node.getRight();
}
}
//线索化的过程
public void threadedNodes(HeroNode node){
if (node==null){
return;
}
// 1.先线索化左子树
threadedNodes(node.getLeft());
// 2、线索化当前节点
// 先处理前驱节点
if(node.getLeft()==null){
// 让当前节点的左指针指向前驱节点
node.setLeft(pre);
node.setLeftType(1);
}
// 处理后继节点
if (pre!=null && pre.getRight()==null){
//让前驱节点的右指针指向当前节点
pre.setRight(node);
// 修改类型
pre.setRightType(1);
}
// 每处理一个节点后,让当前节点是下一个节点的前驱节点
pre=node;
// 3、线索化右子树
threadedNodes(node.getRight());
}
应用
7.3 堆排序
稳定排序和不稳定排序:
排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。
在简单形式化一下,如果Ai = Aj,Ai原来在位置前,排序后Ai还是要在Aj位置前。
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,他的最好最坏平均时间复杂度均为O(nlogn),也是不稳定排序。
堆是完全二叉树,每个节点的值都大于或者等于其左右子节点的值,称为大顶堆【arr[k]>arr[2k+1]&&arr[k]>arr[2k+2]】。左右子节点的值没有大小比较关系
每个节点的值都小于或者等于左右孩子节点的值,称为小顶堆。
堆排序的基本思路:
1) 将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆。
2) 将堆顶元素与末尾元素交换,将最大元素沉到数据末端。
3) 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到有序。
public static void heapSort(int[] arr) {
System.out.println("堆排序");
int temp=0;
//先大顶堆
for (int i=arr.length/2-1; i>=0;i--){
adjustHeap(arr,i,arr.length);
}
System.out.println(Arrays.toString(arr));
//再交换,后循环
for (int j=arr.length-1;j>0;j--){
temp=arr[j];
arr[j]=arr[0];
arr[0]=temp;
adjustHeap(arr,0,j);
}
}
/**
* 这段方法的功能是以i对应的非叶子节点数调整成局部大顶堆 通过递归,最后得到的整体都是大顶堆
*
* @param arr 需要调整的数据
* @param i 非叶子节点的下标索引
* @param length 数组中需要调整的个数。逐渐减少
*/
public static void adjustHeap(int[] arr, int i, int length) {
int temp = arr[i];
//开始调整
for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
//判断是左子节点和右子节点
if (k + 1 < length && arr[k]<arr[k+1]){
k++;
}
if (arr[k]>temp){
//换位置
arr[i]=arr[k];
i=k;
}else {
//这个位置有点不懂? 就是父大于子了,就没有必要再往下找了
break;
}
}
//交换位置
arr[i]=temp;
}
7.3 赫夫曼树
树的带权路径长度规定为所有叶子节点的带权路径长度之和,记为WPL。
权值越大的节点离根节点越近的二叉树才是最优二叉树。
WPL最小的二叉树是赫夫曼树。
构成赫夫曼树的步骤:
1.从小到大排序。可以把每个数据都当成是一个节点,每个节点都是简单的二叉树
2.取出根节点权值最小的两棵二叉树,组成新的二叉树(权值是前两个的和)
【在代码中,要删除原来的,已经保存在了新的二叉树的子节点】
3.再将这个新二叉树,根据权值大小排序。再取前两个,相加,得到新的二叉树。循环。
4.最后只得到一个节点。当从这个节点进行前序遍历,就可以得到一棵赫夫曼树。
public static Node creatHuffmanTree(int[] arr) {
//将arr 改成node并加入nodes list ,再利用重写的比较方法进行排序
//1、遍历,构造出有序的数组
List<Node> nodes = new ArrayList<>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
Collections.sort(nodes);
System.out.println(nodes);
//2.取出根节点权值最小的二叉树
//(1)取出权值最小的节点
//(2)取出第二小的
//(3)构建新的二叉树
//(4)删除处理过的
//(5)将新的加进去
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
nodes.remove(leftNode);
nodes.remove(rightNode);
nodes.add(parent);
}
return nodes.get(0);
}
7.4 赫夫曼编码
广泛应用在数据文件压缩,其压缩率在20%-90%之间。是一种可变字长的编码。
传统上可以使用定长编码,也可以使用一些变长编码,根据频率定义编码。但是在解析时会遇到匹配多重结果,另外就是编码的长度较长。
字符的编码不能是其他字符编码的前缀,这种编码叫前缀编码。即不能匹配到重复的编码。
步骤:
1)字符串,根据字符找到对应的个数,并根据字符出现的次数构建一棵赫夫曼树,次数是权值;d:1 y:1 a:5 等
2)根据以上构成赫夫曼树的步骤,构建赫夫曼树。
3)根据赫夫曼树,给出各个字符,规定编码(前缀编码),向左的路径为0,向右的路径为1;最后得到每个字符的编码。
4)得到字符串对应的编码
注意:
根据排序方法不同,赫夫曼编码也不完全一样,但是WPL时一样的,都是最小的,最后生成的赫夫曼编码的长度也是一样的。
赫夫曼压缩
1.读取文件,到输入流
2.对输入流进行处理,byte[] ,得到赫夫曼表,根据赫夫曼表得到字节流的二进制表示。
3.根据得到的表示,重新转为十进制,并写入输出流 byte[] 赫夫曼编码
4.输出流进行写入,得到最后的压缩结果。
(ObjectInputStream 写入文件的话,记得也写入赫夫曼表,为了解压缩)
解压
1.读取文件,得到输入流
2.对输入流进行处理,进行读取赫夫曼表和赫夫曼编码。
3.根据赫夫曼表对赫夫曼编码进行解码,得到字节数组
4.将解码的得到的byte[ ]写入文件
7.5 二叉排序树(Binary Sort Tree)
任何一个非叶子节点,左节点的值比当前节点的值小,右节点的值比当前节点的值大。 如果有相同的值,放在左右都可以。
创建的话,递归,根据值放在左右即可。
遍历的话,使用中序排序。
重点是在删除:
先找到目标节点,再找到它的父节点。注意:判断是不是只有一个root节点。
1.删除叶子节点:将父节点的左右置空
2.删除只有一个子树的节点:目标节点在父节点的左边,那么父节点的左节点值是目标节点的左或右。同理推。
或者可以说,将目标节点的左节点放在父节点的左或右(是原来目标节点的位置),同理推。
【重点是:如果只有root和它的一个子节点,删除的话没有父节点,所以判断父节点是不是存在,root=target.right/left】
3.删除有两个子树的节点:目标节点的右子树,找最小值,并且替换目标节点的值,并把原来的最小值删除。
7.6 平衡二叉树(AVL树)
因为有一些二叉排序树,可能左边很少,右边很多,严重影响了查询速度,所以进行一个优化。[左右不平衡]
特点:一棵空树或者他的左右两个子树的高度差绝对值不超过1,并且这两个子树都是一个平衡二叉树
代码的重点首先是如何找到子树的高度:
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
//返回左子树的高度
//返回当前节点的高度,以该节点为根节点的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
找到高度以后,进行左旋转或者右旋转。以左旋转为例:
public void leftRotate() {
//1.创建新的节点
Node newNode = new Node(value);
//2.新节点的左子节点还是原来根节点的左子节点,右子节点是根节点的右节点的左节点。
newNode.left = left;
newNode.right = right.left;
//3.把原来的根节点的值替换成根节点的右节点
value = right.value;
//4.现在已经修改的根节点,右边更新
right = right.right;
//5.再更新根节点的左边
left = newNode;
}
调用旋转应该在添加节点的时候,进行判断。
但是有两种特殊情况,就是根节点的子树可能会影响最终的旋转结果。因此,需要分类讨论。
//当添加完一个节点后,如果右边高度-左边高度>1,左旋转
if (rightHeight() - leftHeight() > 1) {
if (right != null && right.leftHeight() > right.rightHeight()) {
right.rightRotate();
leftRotate();
} else {
leftRotate();
}
return;
//必须要,1是没有意义,2是怕进入下边,
} else if (leftHeight() - rightHeight() > 1) {
//可能会出现右旋转后再需要左旋转回来,进入死循环
// 既然是左>右,就先判断左边的子树是不是也是有差距的。
// 如果它的左子树的右子树高度大于左子树的高度,就需要先进行子树的旋转
if (left != null && left.rightHeight() > left.leftHeight()) {
//先左转,再右转
left.leftRotate();
rightRotate();
} else {
rightRotate();
}
}
7.7 多路查找树
问题:二叉树需要加载到内存,如果节点少,那么没问题,
但当节点很多,①构建时,多次进行I/O口操作(数据再数据库或者文件中),非常影响速度。
②节点海量时,二叉树的高度非常大,降低操作速度。
多叉树:每个节点可以有更多的数据项和更多的子节点。例如:2-3数,2-3-4树
B树: 通过重新组织节点,降低树的高度,并且减少I/O读写次数提升效率。
2-3树:
① 所有叶子节点在同一层,只要b树都满足这个条件。
②二节点,要么没有子节点,要么有两个节点。同理,三节点,要么没有,要么有三个。
③2-3树是由二节点和三节点构成的树。
构建的过程中,要满足前两个条件。不满足,就需要拆。先拆上层,如果上层满,就拆本层。反正始终要保证满足前两个条件。
B树 Banlanced,也叫B-树。
B树的阶:
节点最多子节点的个数,如2-3树是3阶。2-3-4树是4阶。
搜索过程:
从根节点开始,对节点内的关键字(有序序列)进行二分查找,命中结束,不命中就继续找儿子节点。直到找到或者已经是叶子节点。
叶子节点和非叶子节点都存放数据,所以搜索可能在非叶子节点结束。搜索性能等同于在关键字全集内进行一次二分查找。
B+树:
B树的变体。
区别:B+树只有在叶子节点命中才结束。等价于关键字全集的二分查找。
所有关键字都出现在叶子节点的链表(是有序的)中,也叫稠密索引。
非叶子节点相当于是叶子节点的索引(稀疏索引),叶子节点是存储数据的数据层。更适合文件索引系统。
B*树:
是在B+树的非根和非叶子节点在增加指向兄弟的指针。B*树分配新节点的概率比B+树要低,空间使用率更高。
8 图
图是一种数据结构,其中节点具有0或者多个相邻元素。
两个节点之间的连接叫边。节点也叫顶点。
图的表示结构:二维数据(邻接矩阵),链表表示(邻接表)
邻接表:
邻接矩阵需要为每个顶点都分配n个边的空间,浪费。邻接表只关心存在的边。例如:0:1 =>2=>4
图遍历,对节点的访问。
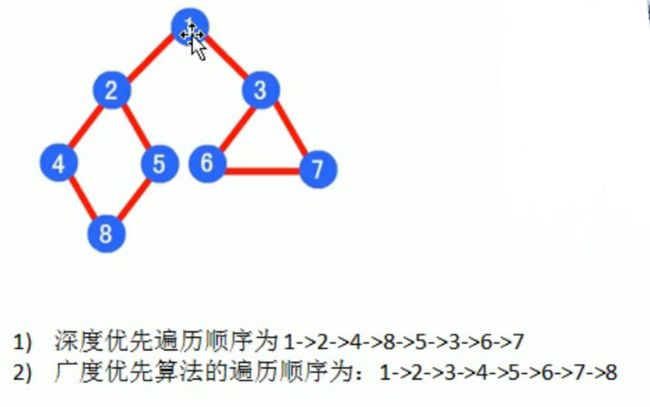
深度优先遍历 Depth Fist Search DFS 纵向挖掘深入
就是从初始节点开始,访问它的第一个邻接节点,再以这个邻接节点为初始节点,访问第一个邻接节点。重复下去。
如果,作为初始节点,但是没有邻接节点或者已经被访问,就返回上一层。以上一层为初始节点,访问第二个邻接节点。
再以第二个邻接节点为初始节点,访问它的第一个邻接节点。重复下去。
//深度优先遍历算法
public void dfs(boolean[] isVisited,int i){
//首先访问该节点,输出
System.out.println(getValueByIndex(i)+"---->");
//将这个节点设为已经访问
isVisited[i]=true;
//查找节点i的第一个邻接节点
int w = getFirstNeighbor(i);(邻接节点为下标i,没有就-1)
while (w!=-1){
if (!isVisited[w]){
dfs(isVisited,w);
}
//如果W已经被访问过,找下一个
w=getNextNeighbor(i,w);
}
}
//其实也就是从第一个开始遍历. 通过对dfs进行一个重载,
private void dfs(){
//遍历所有节点,进行回溯
for (int i=0;i<getNumofVertex();i++){
if (!isVisited[i]){
dfs(isVisited,i);
}
}
}
广度优先遍历 Broad First Search BFS 分层搜索
//对一个节点广度优先遍历 bfs
public void bfs(boolean[] isVisited,int i){
int u;//表示队列的头结点对应下标
int w;//表示邻接节点w
//队列,记录节点的访问顺序
LinkedList<Object> queue = new LinkedList<>();
//先访问这个节点
System.out.println(getValueByIndex(i)+"==>");
isVisited[i] = true;
//将节点加入队列
queue.addLast(i);
while (!queue.isEmpty()){
//取出队列的头节点下标
u = (Integer) queue.removeFirst();
//得到第一个邻接节点的下标
w = getFirstNeighbor(u);
while (w!=-1){
//找到
if (!isVisited[w]) {
System.out.println(getValueByIndex(w)+"==>");
isVisited[w] = true;
//入队
queue.addLast(w);
}
//以u为前一个节点,找w后边的下一个
w = getNextNeighbor(u,w);//体现出广度优先
}
}
}
private void bfs(){
for (int i = 0; i <getNumofVertex(); i++) {
if (!isVisited[i]){
bfs(isVisited,i);
}
}
}