ACM——前缀和二维前缀和与差分的个人理解
前缀和
什么是前缀和
前缀和顾名思义就是指一个数组的某一个下标的(包括该下标)之前的所有数组元素的和。现在我们假设有某一数组a = [1, 2, 3, 4, 5, 6, 7, 8, 9]。其前缀和数组为sum,那么sum数组与a数组对应的关系如下图所示。

由上面的对应关系我们可以得到他们满足如下的公式。
/**
* 一维前缀和
*
* @a 表示原数组
* @sum 表示a数组的一维前缀和
*/
const int maxn = 1e5 + 10;
int a[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int sum[maxn];
void oneDimen(int num) {//num表示数组a的长度
sum[0] = a[0];
for (int i = 1; i < num; i++) {
sum[i] = sum[i - 1] + a[i];
}
}
前缀和使用情况
我们在做题的时候经常会遇到查询问题,例如给出一个数组a,再给出m次查询,每次查询都会给出两个数L,R,分表表示查询区间的左右范围。如果我们只是使用最简单的朴素查询的方法,每次遍历区间,进行m次的查询,这样在题目所给数据范围较小的情况下可以进行,但是当查询次数很大时,其时间复杂度为O(n*m)会使运行TLE,所以我们使用上述的前缀和可以使时间复杂度降低为O(m+n)
int query(int L, int R){
retrun sum[R] - sum[L - 1];
}
差分
什么是差分
差分就是指相邻两个数的差,我们假设存在一个数组,如下图所示

具体代码模板如下:
const int maxn = 1e5 + 10;
int a[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int diff[maxn];
//求出差分数组
void chafen(int num){//num表示原数组的长度
diff[0] = a[0];
for(int i = 1; i < num; i++){
diff[i] = a[i] - a[i - 1];
}
}
//对区间进行加操作
void addarray(int L, int R, int k){
//L和R分别代表对加区间的左右范围,k表示在区间里每个元素加的数字
diff[L] += k;
diff[R + 1] -= k;//这里特别要注意,因为在前面进行区间加后,后面一个数与前面这个数的差变小了,所以要在后面这个数的差分数组减去前面区间所增加的数字。
}
//通过差分数组和原数组a推理得到进行区间加后数组中某一个元素的值
void get_a(){
for(int i = 1; i <= n; i++){
a[i] = doff[i] + a[i - 1];
}
}
差分使用情况
区间加:把数组a[l]到a[r]都加上k,这种操作称为区间加。在进行区间加的操作后得到的数组b,我们对数组b进行查询,但可以发现如果是L——-R非常大的情况下,通过朴素的区间范围内主次累加求和这个操作执行的次数又很多,那时间复杂度会很高。所以可以使用差分的思想来降低复杂度。
二维前缀和
什么是二维前缀和
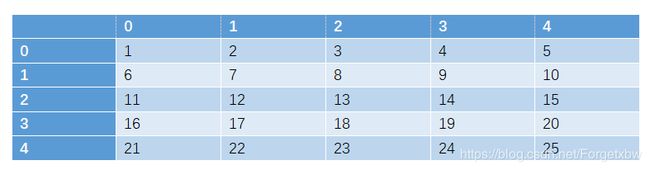
在上图中深蓝色的部分代表的是二维数组的索引,浅蓝色的部分代表的是二维数组的每个元素的值。其二维前缀和如下图所示

前缀和数组里每一个位置都表示原数组当前索引左上方的数字的和。
如上表中的而为前缀和数组:prefixSum[3, 3] = src[0~2, 0~2]的和;
二维前缀和数组的计算步骤如下所示。
可以分为四种情况
- i == 0 && j ==0,只有一个直接赋值即可:prefixSum[0, 0] = a[0, 0]。
- i == 0,最左边的一列,二维前缀和为元素上一行相同列的元素加该数字,公式为prefixSum[0, j] = prefixSum[0, j-1] + a[0, j];
- j == 0,最上面一排,与i == 0类似prefixSum[i, o] = prefixSum[i-1, 0] + a[i, 0];
- i!=0 || j!=0,其公式为 prefixSum[i][j] = prefixSum[i - 1][j] + prefixSum[i][j - 1] + a[i][j] - prefixSum[i - 1][j - 1];
其代码模板如下所示
/**
* 二维前缀和
*
* @param src 原数组
* @return 二维前缀和
*/
const int maxn = 100;
int prefixSum[maxn][maxn];
void twoDimen(int a[][], int n, int m) {//n和m分别代表二维原始数组的行列长度
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i == 0 && j == 0) {//第0个,最左上角
prefixSum[i][j] = a[i][j];
} else if (i == 0) {//第一行,最顶部一行
prefixSum[i][j] = prefixSum[i][j - 1] + a[i][j];
} else if (j == 0) {//第一列,最左边一列
prefixSum[i][j] = prefixSum[i - 1][j] + a[i][j];
} else {//其他
prefixSum[i][j] = prefixSum[i - 1][j] + prefixSum[i][j - 1] + a[i][j] - prefixSum[i - 1][j - 1];
}
}
}
}
二维前缀和的使用情况
一般使用二维前缀和可以求子矩阵的最大值。通过求解出整个矩阵的二维前缀和数组,然后对二位前缀和数组中的元素进行查询,找到其和最大的子矩阵。
二维前缀和的差分
二维前缀和也可以使用差分的形式。方法是和一维类似的,我们也是需要另开一个数组记录修改操作,最后求前缀和时统计修改操作,只是二维每一次操作需要记录4个位置,一维只需要记录2个位置。具体模板代码如下所示。
void chafen(){
for(int i=0;i<m;i++){//m是修改操作次数
int x1,y1,x2,y2,p;
cin>>x1>>y1>>x2>>y2>>p;
b[x1][y1]+=p;
b[x2+1][y2+1]+=p;
b[x2+1][y1]-=p;
b[x1][y2+1]-=p;
}
}
以上部分来自个人理解以及从其他大佬的博客中领悟到的,有些内容可能与其他大佬相似,如有侵权,请及时指出,立马进行修正。有写的不好地方也请及时指出,本人菜鸡,勿喷。
在沉默中爆发,在无声中绽放——xbwcj
