I.常用的数据结构

1.数组和字符串

1.1 字符串转换

例子: 翻转字符串 “algorithm”.

解法: 使用两个指针指向头和尾,往中间进行寻找.

public String reverseStr(String str){
    char[] chars = str.toCharArray();
    int left = 0,right = chars.length-1;
    while (left<=right){
        swap(chars,left,right);
        left++;
        right--;
    }
    //注意使用String.valuOf 方法转为 字符串,不能使用 toString
    return String.valueOf(chars);
}

private char[] swap(char[] chars,int i,int j){
    char temp = chars[i];
    chars[i] = chars[j];
    chars[j] = temp;
    return chars;
}		

数组的优缺点:

• 优:构建简单
• 能在 O(1) 的时间内根据下标找到对应的元素
• 缺:构建必须一段连续的内存空间
• 查询某个元素是否存在,要遍历整个数组 O(n)
• 删除和插入某个元素,耗时,涉及到数组的拷贝 O(n)

应用场景

• 数据元素大小确定,删除/插入操作不多

1.2 例题

例题1:

​ LeetCode 第 242 题：给定两个字符串 s 和 t，编写一个函数来判断 t 是否是 s 的字母异位词。

字母异位词，也就是两个字符串中的相同字符的数量要对应相等.

s 等于 “anagram”，t 等于 “nagaram”，s 和 t 就互为字母异位词。

因为它们都包含有三个字符 a，一个字符 g，一个字符 m，一个字符 n，以及一个字符 r。

思路:

1)使用 哈希表. 使用数组存放每个字符出现的次数,小写字母就26个.

2)直接使用 字母的 ASCII 码作为数组下标 index

3)节约空间:使用 对应字母 - ‘a’ 得到的下标作为 大小为 26 的数组 index

public boolean isAnagram(String s, String t) {
    if(s.length() != t.length()) return false;
    char[] charS = s.toCharArray();
    char[] charT = t.toCharArray();
    int[] ss = new int[256];
    int[] tt = new int[256];
    //英文字母在 256 范围内
    for (int i = 0; i < s.length(); i++) {
        ss[charS[i]] ++;
        tt[charT[i]] ++;
    }
    for (int i = 0; i < ss.length; i++) {
        if(ss[i] != tt[i]) return false;
    }
    return true;
}

//根据都是小写字母 缩小数组大小
public boolean isAnagramI(String s, String t) {
    if(s.length() != t.length()) return false;
    char[] charS = s.toCharArray();
    char[] charT = t.toCharArray();
    int[] ss = new int[26];
    int[] tt = new int[26];
    for (int i = 0; i < charS.length; i++) {
        int indexS = charS[i]-'a';
        ss[indexS]++;
        int indexT = charT[i]-'a';
        tt[indexT]++;
    }
    for (int i = 0; i < ss.length; i++) {
        if(ss[i] != tt[i]) return false;
    }
    return true;
}

//使用 只用一个数组的方式完成比较
public boolean isAnagramII(String s, String t) {
    if(s.length() != t.length()) return false;
    char[] charS = s.toCharArray();
    char[] charT = t.toCharArray();
    int[] tt = new int[26]; //只用一个数组 即可
    for (int i = 0; i < charS.length; i++) {
        int indexS = charS[i]-'a';
        tt[indexS]++;
        int indexT = charT[i]-'a';
        tt[indexT]--; // 最后判断 tt 是否为 0
    }
    for(int a:tt){
        if(a!=0) return false;
    }
    return true;
}

2. 链表

2.1 基本介绍

优缺点**

• 优:能够灵活分配内存空间
• 能够在 O(1) 的时间内完成插入/删除操作.前提是该元素的前一个元素已知
• 缺:不能像数组那样通过下标迅速读取元素,每次都要遍历获取
• 查询第 k 个元素需要 O(k) 时间

应用场景:

• 数据元素个数不确定,而且需要经常进行插入/删除操作

2.2常用方法

使用快慢指针:

• 链表的翻转
• 寻找倒数第 k 个元素
• 寻找链表中间位置的元素
• 判断链表是否有环

构建一个虚假的链表头:

• 

2.3 例题(未完成)

例题1:

​ LeetCode 第 25 题：给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

思路:

​ 不会,看不懂 烦死个人

参考:以后再看

https://leetcode-cn.com/problems/reverse-nodes-in-k-group/solution/tu-jie-kge-yi-zu-fan-zhuan-lian-biao-by-user7208t/

3. 栈

3.1 基本概念

特点: 先进后出(FILO,First In Last Out)

实现: 利用一个单链表来实现栈的数据结构.因为只针对栈顶元素进行操作,所以借用单链表的头就能让所有栈的操作在 O(1) 的时间内完成.

​ 如果打算使用数组和指针来实现相似的效果,那么一旦数组长度发生变化,时间复杂度就不再是 O(1)了

3.2 应用场景

• 解决某个问题时候,只关心最近一次的操作,并且操作完成之后,需要向前查找到更前一次的操作.

3.3 例题

栈是 leetcode 中等难度偏上题目经常使用的数据结构.

例题1

LeetCode 第 20 题：给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。

左括号必须以正确的顺序闭合。

注意：空字符串可被认为是有效字符串。

思路:

• 判断是左侧括号入栈,
• 如果是右侧括号,则出栈和即将入栈的比较,
• 相等,则不入栈
• 不相等,返回false
• 注意:栈空的判断

//20  https://leetcode-cn.com/problems/valid-parentheses/
// 8 ms 我写的就是个垃圾
public boolean isValid(String s) {
    if (s.length() == 0) return true;
    char[] chars = s.toCharArray();
    Stack<Character> stack = new Stack<>();

    for (int i = 0; i < chars.length; i++) {
        String a = chars[i]+"";
        if (a.equals(")") || a.equals("}") || a.equals("]")){
            if(stack.isEmpty()) return false;
            String pop = stack.pop()+"";
            if(a.equals(")")){
                if (!pop.equals("(")) return false;
            }
            else if(a.equals("]")){
                if (!pop.equals("[")) return false;
            }
            else if(a.equals("}")){
                if (!pop.equals("{")) return false;
            }
            continue;
        }
        stack.push(chars[i]);
    }
    if(stack.isEmpty()) return true;
    return false;
}

//1 ms
public boolean isValidI(String s) {
    if(s.isEmpty())
        return true;
    Stack<Character> stack=new Stack<Character>();
    for(char c:s.toCharArray()){
        if(c=='(')
            stack.push(')');
        else if(c=='{')
            stack.push('}');
        else if(c=='[')
            stack.push(']');
        else if(stack.empty()||c!=stack.pop())
            return false;
    }
    if(stack.empty())
        return true;
    return false;
}

例题2

​ LeetCode 第 739 题：根据每日气温列表，请重新生成一个列表，对应位置的输入是你需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用 0 来代替。

思路:

• 解法一: 暴力破解—两个for 循环遍历
• 解法二: 利用栈
• 参考5分钟学算法的讲解

//739 https://leetcode-cn.com/problems/daily-temperatures/
public int[] dailyTemperatures(int[] T) {
    int[] ret = new int[T.length];
    for (int i = 0; i < T.length-1; i++) {
        int count = 0;
        for (int j = i+1; j < T.length; j++) {
            if(T[i]<T[j]) {
                count++;
                ret[i] = count;
                count = 0;
                break;
            }else
                count++;
        }
    }
    ret[T.length-1] = 0;
    return ret;
}

//https://leetcode-cn.com/problems/daily-temperatures/solution/leetcode-tu-jie-739mei-ri-wen-du-by-misterbooo/
public int[] dailyTemperaturesI(int[] T) {
    int[] ret = new  int[T.length];
    Stack<Integer> stack = new Stack();

    for (int i = 0; i < T.length; i++) {
        if (stack.isEmpty()){
            stack.push(i);
        }
        else {
            while (!stack.isEmpty() && T[i]>T[stack.peek()] ){
                Integer actualPop = stack.pop();
                ret[actualPop] = i-actualPop;
            }
            stack.push(i);
        }
    }
    return  ret;
}

public int[] dailyTemperaturesII(int[] T) {
    int[] ret = new  int[T.length];
    Stack<Integer> stack = new Stack();

    for (int i = 0; i < T.length; i++) {
        while (!stack.isEmpty() && T[i]>T[stack.peek()] ){
            Integer actualPop = stack.pop();
            ret[actualPop] = i-actualPop;
        }
        stack.push(i);
    }
    return  ret;
}

例题3(未完成)

• 求解算术表达式的结果（LeetCode 224、227、772、770)
• 求解直方图里最大的矩形区域（LeetCode 84）

4. 队列(Queue)

特点

• 先进先出(FIFO)
• 只允许在队头查看和删除数据
• 只允许在队尾查看和添加数据

实现

• 借助双链表实现队列
• 双链表的头指针允许在队列头查看和删除数据
• 双链表的尾指针允许在队尾查看和添加数据

应用场景

• 按照一定的顺序处理数据
• 且该数据的数据量在不断的变化
• 在 BFS 中,是运用队列最多的地方

5.双端队列(Deque)

特点

• 允许在队列的头和尾两端都能在 O(1) 的时间内进行数据 查看 添加 删除

实现

• 利用双链表实现

应用场景

• 用来实现一个长度动态变化的窗口 / 连续区间

Java 中 对应的数据结构

public interface Queue<E> extends Collection<E> 
    
public interface Deque<E> extends Queue<E> 
    
public class LinkedList<E>
    extends AbstractSequentialList<E>
    implements List<E>, Deque<E>, Cloneable, 	
	java.io.Serializable

例题

​ LeetCode 第 239 题：给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字，滑动窗口每次只向右移动一位。返回滑动窗口最大值。

public int[] maxSlidingWindow(int[] nums, int k) {
    if(nums.length == 0) return nums;
    int[] result = new int[nums.length-k+1];
    int index = 0;
    Deque<Integer> deque = new LinkedList<>();

    for (int i = 0; i < nums.length; i++) {
        //step1:头 - 移除队头,保证窗口的大小范围有效
        //使用下标 好像更容易理解
        if (i >= k){
            if (deque.peekFirst() == i-k){
                //表示窗口长度此时为 k 好像是
                //使用这个判断,能确保窗口大小一直满足条件,好好理解
                deque.pollFirst();
            }
        }
        //step2:尾 - 移除当前值大于尾部的值 (可能会一直移除)
        while (!deque.isEmpty() && nums[i]>nums[deque.getLast()]){
            deque.pollLast();
        }
        //step3:尾 - 当前值加入队列
        deque.addLast(i);
        //step4:头 - 返回当前的队头的最大值
        if (i >= k-1){
            result[index++] = nums[deque.peekFirst()];
        }
    }
    return result;
}

6. 树

6.1 树的形状

• 普通二叉树 平衡二叉树 完全二叉树 二叉搜索树
• 四叉树
• 多叉树
• 红黑树 自平衡二叉搜索树

6.2 树的遍历

• 前序遍历(根左右)

  应用场景:

  ​ 在树中进行搜索以及创建一棵新的树

• 中序遍历(左根右)

  应用场景:

  ​ 最常见的二叉搜索树,由于二叉搜索树的性质就是左孩子小于根节点,根节点小于右孩子.对二叉树进行中序遍历的时候是按顺序进行的

• 后序遍历(左右根)

  应用场景:

  ​ 在对某个结点进行分析的时候,需要左右子树的信息.收集信息的操作是从底部不断往上进行的.好比修剪一棵树的叶子,修剪方法是:从外面不断地往根部将叶子一片一片修剪掉.

6.3 例题

例题1(LeetCode要订阅)

上面的输出为: 4

例题2

​ LeetCode 第 230 题：给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

int count = 1;
int result = 0;
public int kthSmallest(TreeNode root, int k) {
    //中序遍历
    if (root == null) {
        return 0;
    }
    //提前结束后面的递归,相当于剪枝
    if (count >= k+1) {
        return 0;
    }
    kthSmallest(root.left,k);
    //print root
    if(count == k){
        result = root.val;
    }
    count++;
    kthSmallest(root.right,k);
    return result;
}

7. 优先队列

7.1 特点

• 能够保证每次取出的元素都是队列中优先级别最高的.

• 优先级别可以自定义.如:数据的数值越大/小,优先级越高.

• 优先队列的本质是一个二叉堆结构,利用一个数组结构来实现的完全二叉树.

  换句话说:优先队列的本质是一个数组,数组里面的每个元素既有可能是其他元素的父节点,也可能是其他元素的子节点

  数组第一个元素拥有最高的优先级别

7.2 应用场景

• 从一堆杂乱无章的数据中按照一定的顺序/优先级,逐步的筛选出部分/全部数据

7.3 实现

优先队列的两个基本操作:

• 向上筛选(sift up/bubble up)

  当有新的数据加入到优先队列中,新的数据首先放在二叉堆的底部

  然后不断进行向上筛选操作,即如果发现该**数据的优先级别比父节点的优先级别还高,**那么就和父节点元素交换.继续向上进行比较,直到无法进行交换位为止.

  时间复杂度: O(logk) 即树的高度

• 向下筛选(sift down/bubble down)

  当堆顶元素被取出时,要更新堆顶的元素作为下一次按照优先级顺序被取出的对象, 需要 将 堆底部的元素放置到堆顶,然后不断的对它进行向下筛选操作.

  将该元素和它的两个孩子节点对比优先级,如果优先级最高的是其中一个孩子,就将该元素和那个孩子交换,反复进行,直到无法交换为止.

  时间复杂度: O(logk) 即树的高度

7.4 例题

例题1

找出数组前 K 大 的数

//215 
// 8 ms 使用大顶堆
public int findKthLargest(int[] nums, int k) {

    Queue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2-o1;
        }
    });
    for (int i = 0; i < nums.length; i++) {
        priorityQueue.add(nums[i]);
    }

    for (int i = 0; i < k-1; i++) {
        priorityQueue.poll();
    }
    return priorityQueue.poll();
}

// 19 ms 使用快排 nlogn
public int findKthLargestI(int[] nums, int k) {
    //快排思想
    int partition = partition(nums, 0, nums.length - 1);

    /**
         * 长度为 6
         * 求 第 2(k) 大 就是求 第 5(nums.length-k+1) 小
         *
         */
    int kthMax = nums.length-k+1;

    while (partition != kthMax-1){
        if (partition < kthMax-1){
            partition = partition(nums,partition+1,nums.length-1);
        }else {
            partition = partition(nums,0,partition-1);
        }
    }
    return nums[partition];
}

//返回的ret就是 分区点的下标 分区点左边都小于 array[ret],右边都大于 array[ret]
private int partition(int[] array,int p,int r){
    int point = array[r];
    int i=p,j=p;
    for (;j<r;j++){
        if (array[j] <= point){
            if(i == j){
                i++;
            }else {
                swapArray(array,i,j);
                i++;
            }
        }
    }
    swapArray(array,i,j);
    return i;


    /*int i =p;
        int j= p;
        int pivot = array[r];
        for(;j
}
private void swapArray(int[] array,int i,int j){
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}		

例题2

LeetCode 第 347 题：给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

public int[] topKFrequent(int[] nums, int k) {

    Map<Integer,Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        map.put(nums[i],map.getOrDefault(nums[i],0)+1);
    }

    List<Map.Entry<Integer,Integer>> list = new ArrayList<>(map.entrySet());
    Collections.sort(list, new Comparator<Map.Entry<Integer, Integer>>() {
        @Override
        public int compare(Map.Entry<Integer, Integer> o1, Map.Entry<Integer, Integer> o2) {
            return o2.getValue()-o1.getValue();
        }
    });

    int[] result = new int[k];
    for (int i = 0; i < k; i++) {
        result[i] = list.get(i).getKey();
    }
    return result;
}
// O(nlogn) 使用小顶堆进行优化
public int[] topKFrequentI(int[] nums, int k) {

    Map<Integer,Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        map.put(nums[i],map.getOrDefault(nums[i],0)+1);
    }

    //存入 key ,根据 key 获取的键 进行排序
    Queue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            //                return map.get(o2)-map.get(o1);
            //使用小顶堆,后面方便优化
            return map.get(o1)-map.get(o2);
        }
    });

    for (Integer key:map.keySet()){
        // O(logn) 的操作
        //            queue.add(key);
        // O(logK) 的操作
        //注意:这个地方不能 = 
        if (queue.size() < k){
            queue.add(key);
        }else {
            if (map.get(key) > map.get(queue.peek())){
                queue.poll();
                queue.add(key);
            }
        }

    }
    //取出 k 个
    int[] result = new int[k];
    for (int i = 0; i < k; i++) {
        result[i] = queue.poll();
    }
    return result;
}

8. 图

8.1 基本知识点

8.2 相关算法

8.3 必会知识点

• 环的检测
• 二部图的检测
• 树的检测
• 拓扑排序
• 最短路径算法: 能区分特点,在合适的场合选择使用合适的算法

8.4 例题(未完成)

LeetCode 第 785 题：给定一个无向图 graph，当这个图为二部图时返回 true。

9. 前缀树(Trie)

9.1 应用场景

• 前缀树被广泛应用于字典查找中,也被称为字典树
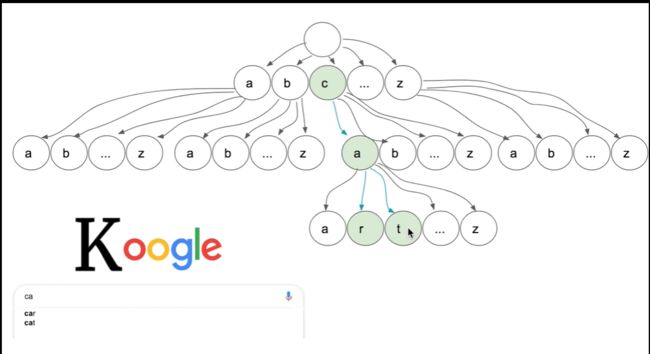
• 网站上的搜索框会罗列出以搜索文字作为开头的相关搜索信息，这里运用了前缀树进行后端的快速检索。
• 汉字拼音输入法的联想输出功能也运用了前缀树。

9.2 实例

例1

​ 举例：给定一系列字符串，这些字符串构成了一种字典，要求你在这个字典当中找出所有以“ABC”开头的字符串。

思路

• 解法一:暴力搜索.直接遍历一遍字典,然后判断每个字符串是否是’ABC’开头.假设 N 个单词,对比的是任意的开头,长度为M, 时间复杂度为 O(M*N)
• 解法二:使用前缀树对字段存储进行优化.可以将时间复杂度将为 O(M).M表示字典中最长的那个单词的字符个数.

例2

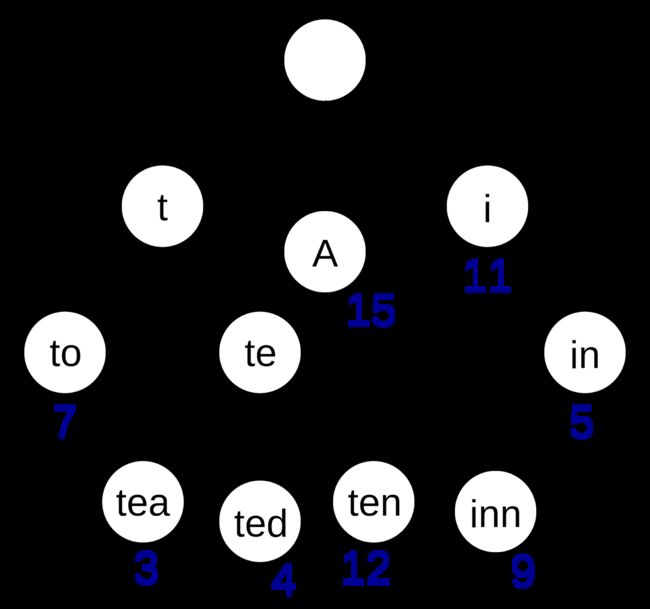
假如有一个字典，字典里面有如下词：“A”，“to”，“tea”，“ted”，“ten”，“i”，“in”，“inn”，每个单词还能有自己的一些权重值，那么用前缀树来构建这个字典将会是如下的样子：

性质

• 每个节点至少包括两个属性

  children: 数组或者集合,罗列出每个分支中包含的所有字符

  isEnd: 布尔值, 表示该节点是否为某字符串的结尾

• 前缀树的根节点是空的

  空 是指: 只利用这个节点的 children 属性,即只关心在这个字典里,有哪些打头的字符.

• 除了根节点,其他所有节点都可能是单词的结尾,叶子节点一定是单词的结尾

9.3 实现

基于数组实现

//208  
//https://leetcode-cn.com/problems/implement-trie-prefix-tree/
class Trie {

    TrieNode root = null;
    /** Initialize your data structure here. */
    public Trie() {
        root = new TrieNode();
    }

    /** Inserts a word into the trie. */
    public void insert(String word) {
        TrieNode cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            if(cur.children[c -'a'] == null){
                //直接插入
                TrieNode child = new TrieNode();
                cur.children[c - 'a'] = child;
            }
            //已经存在了，则插入
            cur = cur.children[c - 'a'];
        }
        //注意将最后置为 true
        cur.isWord = true;
    }

    /** Returns if the word is in the trie. */
    public boolean search(String word) {
        TrieNode cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            if (cur.children[c - 'a'] ==null){
                return false;
            }
            cur = cur.children[c - 'a'];
        }
        //要判断是单词结尾才行
        return cur.isWord;
    }

    /** Returns if there is any word in the trie that starts with the given prefix. */
    public boolean startsWith(String prefix) {
        TrieNode cur = root;
        for (int i = 0; i < prefix.length(); i++) {
            char c = prefix.charAt(i);
            if (cur.children[c - 'a'] == null){
                return false;
            }
            cur = cur.children[c - 'a'];
        }
        return true;
    }

    class TrieNode{
        public boolean isWord;
        public TrieNode[] children;
        public TrieNode(){
            isWord = false;
            children = new TrieNode[26];
        }
    }
}

基于Map实现

/**
  * 使用 map 实现前缀树
  */
class TrieNode{
    public boolean isWord;
    public Map<Character,TrieNode> chlidren;
    public TrieNode(){
        isWord = false;
        chlidren = new HashMap<>();
    }
}

class Trie {
    TrieNode root = null;
    /** Initialize your data structure here. */
    public Trie() {
        root = new TrieNode();
    }

    /** Inserts a word into the trie. */
    public void insert(String word) {
        TrieNode cur = root;
        for (int i = 0; i < word.length(); i++) {
            if (!cur.chlidren.containsKey(word.charAt(i))){
                TrieNode temp = new TrieNode();
                //不存在则加入，要知道如何加入
                cur.chlidren.put(word.charAt(i),temp);
            }
            cur = cur.chlidren.get(word.charAt(i));
        }
        cur.isWord = true;
    }

    /** Returns if the word is in the trie. */
    public boolean search(String word) {
        TrieNode cur = root;
        for (int i = 0; i < word.length(); i++) {
            if (!cur.chlidren.containsKey(word.charAt(i))){
                return false;
            }
            cur = cur.chlidren.get(word.charAt(i));
        }
        return cur.isWord;
    }

    /** Returns if there is any word in the trie that starts with the given prefix. */
    public boolean startsWith(String prefix) {
        TrieNode cur = root;
        for (int i = 0; i < prefix.length(); i++) {
            if (!cur.chlidren.containsKey(prefix.charAt(i))){
                return false;
            }
            cur = cur.chlidren.get(prefix.charAt(i));
        }
        return true;
    }
}

9.4 例题

LeetCode 第 212 题：给定一个二维网格 board 和一个字典中的单词列表 words，找出所有同时在二维网格和字典中出现的单词。

/**
* 212
* https://leetcode-cn.com/problems/word-search-ii/
*/
public List<String> findWords(char[][] board, String[] words) {
    Trie212 trie = new Trie212();
    for (String word : words) {
        trie.insert(word);
    }
    List<String> result = new LinkedList<>();

    StringBuilder path = new StringBuilder();
    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[0].length; j++) {
            dfs(i, j, board, trie.root, path, result);
        }
    }
    return result;
}

private void dfs(int i, int j, char[][] board, TrieNode root, StringBuilder path, List<String> result) {
    //到达终点状态-->判断是否是单词的结尾
    if (root.isWord) {
        result.add(path.toString());
        //找到了就置为 false 防止重复搜索
        root.isWord = false;
    }
    //越界
    if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) {
        return;
    }
    char temp = board[i][j];
    // 剪枝-->如果不是单词
    if (temp == '#' || root.children[temp - 'a'] == null) {
        return;
    }
    root = root.children[temp - 'a'];
    //是单词的一部分

    //不是结尾继续搜索
    //标记已经搜索过的字符
    board[i][j] = '#';
    dfs(i + 1, j, board, root, path.append(temp), result);
    path.deleteCharAt(path.length() - 1);

    dfs(i - 1, j, board, root, path.append(temp), result);
    path.deleteCharAt(path.length() - 1);

    dfs(i, j + 1, board, root, path.append(temp), result);
    path.deleteCharAt(path.length() - 1);

    dfs(i, j - 1, board, root, path.append(temp), result);

    board[i][j] = temp;
    path.deleteCharAt(path.length() - 1);
    //System.out.println(path);
}


/**
* 这个好像好理解一点
* 注意：
*      在递归时 +1之类的操作，使用 +1，不用 ++
* https://leetcode-cn.com/problems/word-search-ii/
*/
public List<String> findWordsI(char[][] board, String[] words) {
    Trie212 trie = new Trie212();
    for (String word : words) {
        trie.insert(word);
    }
    List<String> result = new LinkedList<>();

    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[0].length; j++) {
            dfsI(i, j, board, trie.root, "", result);
        }
    }
    return result;
}

private void dfsI(int i, int j, char[][] board, TrieNode root, String path, List<String> result) {
    //到达终点状态-->判断是否是单词的结尾
    if (root.isWord) {
        result.add(path);
        //找到了就置为 false 防止重复搜索
        root.isWord = false;
    }
    //越界
    if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) {
        return;
    }
    char temp = board[i][j];
    // 剪枝-->如果不是单词
    if (temp == '#' || root.children[temp - 'a'] == null) {
        return;
    }
    root = root.children[temp - 'a'];
    //是单词的一部分

    //不是结尾继续搜索
    //标记已经搜索过的字符
    board[i][j] = '#';
    dfsI(i + 1, j, board, root, path+temp, result);
    dfsI(i - 1, j, board, root, path+temp, result);
    dfsI(i, j + 1, board, root, path+temp, result);
    dfsI(i, j - 1, board, root, path+temp, result);
    board[i][j] = temp;
}

10.线段树

10.1 引入

10.2 实现

10.3 例题(未完成)

LeetCode 第 315 题：给定一个整数数组 nums，按要求返回一个新数组 counts，使得数组 counts 有该性质——counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

11. 树状数组

11.1 实现

11.2 特点

• 使用数组来表示多叉树的结构
• 树状数组的第一个元素是空节点
• 如果节点 tree[y] 是 tree[x] 的父节点,那么满足条件: y= x-( x&(-x) )

11.3 例题(未完成)

LeetCode 第 308 题，求一个动态变化的二维矩阵里，任意子矩阵里的数的总和。