Reasoning with Sarcasm by Reading In-between
Reasoning with Sarcasm by Reading In-between
click here:文章下载
方法综述:
本文提出了新的模型SIARN(Singal-dimensional Intra-Attention Recurrent Networks)和MIARN(Multi-dimensional Intra-Attention Recurrent Networks)。
先给出一个定义,关系得分 s i , j s_{i,j} si,j表示单词 w i w_i wi、 w j w_j wj间的信息关联程度。二者的区别仅在于,SIARN中只考虑单词对间的一种内在关系, s i , j s_{i,j} si,j是个标量;而MIARN考虑单词对间的多种(k种)内在关系, s i , j s_{i,j} si,j是个k维向量,再将其融合为一个标量。
模型中包含三个子模型:Singal/Multi-dimensional Intra-Attention、LSTM、Prediction Layer:
Singal/Multi-dimensional Intra-Attention:通过单词对间的信息,得到句子的Intra-Attentive Representation
LSTM:通过句子的序列信息,得到句子的Compositional Representation
Prediction Layer: 融合两种信息表示,进行二分类预测
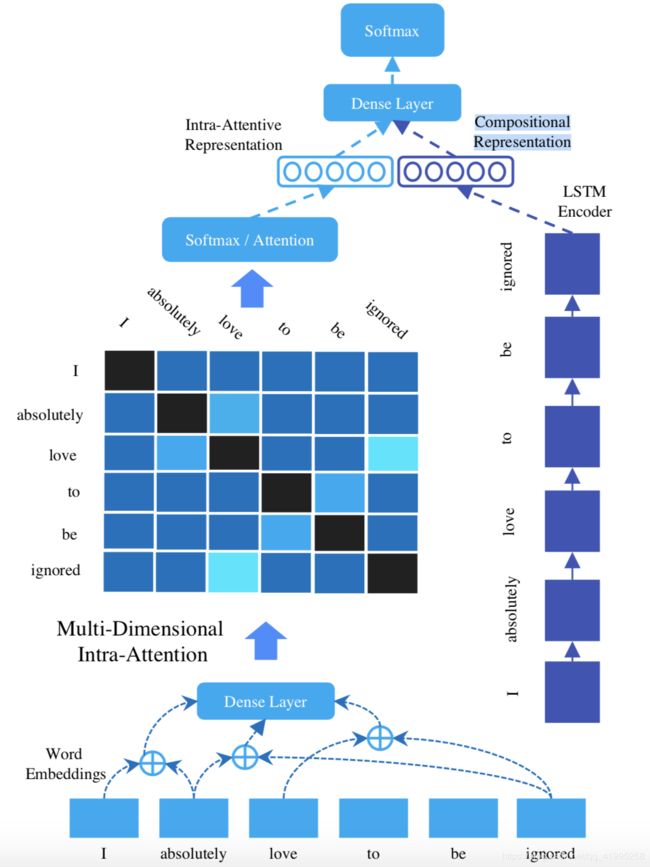
各模型算法:
Singal/Multi-dimensional Intra-Attention
Sigal-dimensional:
s i , j = W a ( [ w i ; w j ] ) + b a ⟹ s i , j ∈ R s_{i,j}=W_a([w_i;w_j])+b_a \implies s_{i,j} \in R si,j=Wa([wi;wj])+ba⟹si,j∈R 标量
W a ∈ R 2 n × 1 , b a ∈ R ; W_a \in R^{2n \times 1},b_a \in R; Wa∈R2n×1,ba∈R;
Multi-dimensional:
s i , j ^ = W q ( [ w i ; w j ] ) + b q ⟹ s i , j ^ ∈ R k \hat{s_{i,j}}=W_q([w_i;w_j])+b_q \implies \hat{s_{i,j}} \in R^k si,j^=Wq([wi;wj])+bq⟹si,j^∈Rk k维向量
W q ∈ R 2 n × k , b q ∈ R k ; W_q \in R^{2n \times k},b_q \in R^k; Wq∈R2n×k,bq∈Rk;
s i , j = W p ( R e L U ( s i , j ^ ) ) + b p s_{i,j}=W_p(ReLU(\hat{s_{i,j}}))+b_p si,j=Wp(ReLU(si,j^))+bp
W p ∈ R k × 1 , b p ∈ R ; W_p \in R^{k \times 1},b_p \in R; Wp∈Rk×1,bp∈R;
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ \Downarrow \Downarrow \Downarrow \Downarrow \Downarrow \Downarrow \Downarrow \Downarrow \Downarrow \Downarrow ⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓
s i , j = W p ( R e L U ( W q ( [ w i ; w j ] ) ) ) + b p s_{i,j}=W_p(ReLU(W_q([w_i;w_j])))+b_p si,j=Wp(ReLU(Wq([wi;wj])))+bp
W q ∈ R 2 n × k , b q ∈ R k , W p ∈ R k × 1 , b p ∈ R ; W_q \in R^{2n \times k},b_q \in R^k,W_p \in R^{k \times 1},b_p \in R; Wq∈R2n×k,bq∈Rk,Wp∈Rk×1,bp∈R;
从而,对于长度为 l l l的句子,可以得到对称矩阵 s ∈ R l × l s \in R^{l \times l} s∈Rl×l。
对矩阵s进行row-wise max-pooling,即按行取最大值,得到attention vector: a ∈ R l a \in R^l a∈Rl
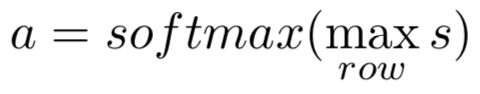
有了权重向量a,便可以对句子单词进行加权求和,得到Intra-Attentive Representation: v a ∈ R n v_a \in R^n va∈Rn:
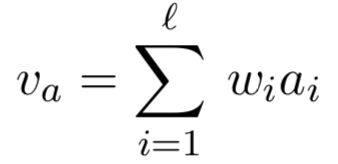
LSTM
LSTM的每个时间步输出 h i ∈ R d h_i \in R^d hi∈Rd,可以表示为:
h i = L S T M ( w , i ) , ∀ i ∈ [ 1 , . . . , l ] h_i=LSTM(w,i),\forall i \in [1,...,l] hi=LSTM(w,i),∀i∈[1,...,l]
本文使用LSTM的最后时间步输出,作为Compositional Representation: v c ∈ R d v_c \in R^d vc∈Rd
v c = h l v_c=h_l vc=hl
d d d是LSTM隐藏层单元数, l l l是句子的最大长度。
Prediction Layer
融合上述得到的Intra-Attentive Representation v a ∈ R n v_a \in R^n va∈Rn、Compositional Representation v c ∈ R d v_c \in R^d vc∈Rd,得到融合表示向量 v ∈ R d v \in R^d v∈Rd,再进行二分类输出 y ^ ∈ R 2 \hat{y} \in R^2 y^∈R2:
v = R e L U ( W z ( [ v a ; v c ] ) + b z ) v=ReLU(W_z([v_a;v_c]) + b_z) v=ReLU(Wz([va;vc])+bz)
y ^ = S o f t m a x ( W f v + b f ) \hat{y}=Softmax(W_fv+b_f) y^=Softmax(Wfv+bf)
其中, W z ∈ R ( d + n ) × d , b z ∈ R d , W f ∈ R d × 2 , W f ∈ R d × 2 , b f ∈ R 2 W_z \in R^{(d+n) \times d},b_z \in R^d,W_f \in R^{d \times 2},W_f \in R^{d \times 2}, b_f \in R^2 Wz∈R(d+n)×d,bz∈Rd,Wf∈Rd×2,Wf∈Rd×2,bf∈R2
训练目标:
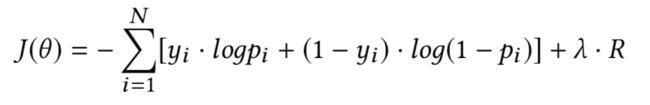

待学习参数: θ = { W p , b p , W q , b q , W z , b z , W f , b f } \theta = \{W_p,b_p,W_q,b_q,W_z,b_z,W_f,b_f\} θ={Wp,bp,Wq,bq,Wz,bz,Wf,bf}
超参数: k , n , d , λ k, n, d, \lambda k,n,d,λ