Drop Voicing

链接：https://ac.nowcoder.com/acm/contest/5670/D
来源：牛客网

题目描述
Inaka composes music. Today’s arrangement includes a chord of nn notes that are pairwise distinct, represented by a permutation $p_{1\dots n}$ of integers from $1$ to $n$ (inclusive) denoting the notes from the lowest to the highest.

Her friend, Miyako, sneaks in and plays a trick by altering the chord with the following two operations:

• Drop-2: Take out the second highest note and move it to the lowest position, i.e. change the permutation to $p_{n-1},p_1,p_2,\dots ,p_{n-3},p_{n-2},p_n$.
• Invert: Take out the lowest note and move it to the highest position, i.e. change the permutation to $p_2,p_3,\dots ,p_{n-1},p_n,p_1$.

Any number of consecutive Drop-2 operations is considered a multi-drop. Miyako would like to change the permutation to an ordered permutation, $1,2,\dots ,n$, in the fewest number of multi-drops possible. Please help her find the number of multi-drops needed.

输入描述:
The first line contains an integer $n$ ($2\le n\le 500$) — the number of notes.

The second line contains $n$ space-separated integers $p_1,p_2,\dots ,p_n$ — the original permutation of notes.

The input guarantees each integer from $1$ to $n$ (inclusive) appears in the permutation exactly once.
输出描述:
Output one integer — the number of multi-drops required to change the permutation to an ordered one.
示例1

输入
6
2 4 5 1 3 6
输出
2

说明
An optimal solution with two multi-drops is:

• Invert, $5$ times, changing the permutation to $6,2,4,5,1,3$;
• Drop-2, $3$ times, changing the permutation to $4,5,1,6,2,3$;
• Invert, $4$ times, changing the permutation to $2,3,4,5,1,6$;
• Drop-2, $1$ time, changing the permutation to $1,2,3,4,5,6$.

示例2

输入
8
8 4 7 3 6 2 5 1
输出
5

有一个结论，只需要一次multi-drops和任意次Invert就可以把任意一个数移到任意一个位置而不会改变其他任意两个数之间的相对位置。
证明如下：
将$a$移到$b$，$c$之间，而不改变其他数的相对位置。
由于可以通过若干次Invert操作改变$a$与$b$，$c$的相对位置，因此不妨设$a$在$b$，$c$前面。

如下图操作：
1.Invert

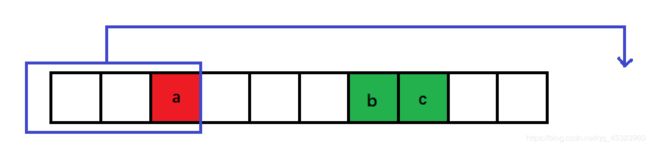
2.multi-drops

3.Invert


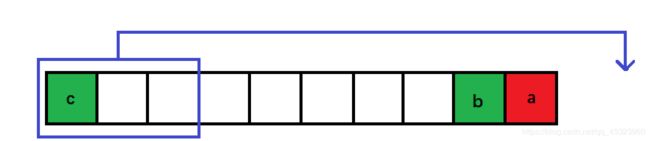
将序列首位相接连成环，Invert操作相当于改变序列的起始位置，因此求环形序列的最长上升子序列，然后剩余元素移到相对位置一定是最优解，即$ans=min(n-LIS)$。时间复杂度为$O(n^{2}logn)$。

#include 

#define si(a) scanf("%d",&a)
#define sl(a) scanf("%lld",&a)
#define sd(a) scanf("%lf",&a)
#define sc(a) scanf("%c",&a)
#define ss(a) scanf("%s",a)
#define pi(a) printf("%d\n",a)
#define pl(a) printf("%lld\n",a)
#define pc(a) putchar(a)
#define ms(a) memset(a,0,sizeof(a))
#define repi(i, a, b) for(register int i=a;i<=b;++i)
#define repd(i, a, b) for(register int i=a;i>=b;--i)
#define reps(s) for(register int i=head[s];i;i=Next[i])
#define ll long long
#define ull unsigned long long
#define vi vector
#define pii pair
#define mii unordered_map
#define msi unordered_map
#define lowbit(x) ((x)&(-(x)))
#define ce(i, r) i==r?'\n':' '
#define pb push_back
#define fi first
#define se second
#define INF 0x3f3f3f3f
#define pr(x) cout<<#x<<": "<
using namespace std;

inline int qr() {
    int f = 0, fu = 1;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-')fu = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        f = (f << 3) + (f << 1) + c - 48;
        c = getchar();
    }
    return f * fu;
}

const int N = 1000;

int tmp[N], len;

int LIS(int *a, int n) {
    tmp[1] = a[1], len = 1;
    repi(i, 2, n) {
        if (a[i] > tmp[len]) tmp[++len] = a[i];
        else tmp[lower_bound(tmp + 1, tmp + len, a[i]) - tmp] = a[i];
    }
    return len;
}

int n, a[N << 1], ans = INF;

int main() {
    n = qr();
    repi(i, 1, n)a[i + n] = a[i] = qr();
    repi(i, 0, n - 1)ans = min(ans, n - LIS(a + i, n));
    pi(ans);
    return 0;
}