室内定位Matlab程序笔记
程序: fix( * )
功能:Y = fix(X) 将 X 的每个元素朝零方向四舍五入为最近的整数。对于正方向的 X,fix 的行为与 floor 相同。对于负方向的 X,fix 的行为与 ceil 相同。
>> X = [-1.9 -3.4; 1.6 2.5; -4.5 4.5]
>> X = 3×2
-1.9000 -3.4000
1.6000 2.5000
-4.5000 4.5000
>> Y = fix(X)
>> Y = 3×2
-1 -3
1 2
-4 4
程序: ones( * )
功能:ones()是产生一个全1矩阵
示例:
>> ones(3)
ans =
1 1 1
1 1 1
1 1 1
>> ones(3,4)
ans =
1 1 1 1
1 1 1 1
1 1 1 1
程序: 变量(index)
功能:变量名(索引值)为对变量(向量/矩阵)指定位置进行索引(初始值为1,而非0),注意时圆括号
示例:
>> b = [1 2 3 4 5]
b =
1 2 3 4 5
>> b(3)
ans =
3
>> a = [1 2 3;4 5 6]
a =
1 2 3
4 5 6
>> a(2,1)
ans =
4
程序: 变量([ ])
功能:变量名([ 索引值 ])为对变量(向量/矩阵)指定子序列进行索引(初始值为1,而非0),索引时按照列优先
示例:
>> b([3:5 1:2])
ans =
3 4 5 1 2
程序:find( X )
功能:find()函数的功能是找到向量或者矩阵中不为0的元素,返回其索引下标;如果需要找到其中满足一定条件的元素时,可在括号内指定
示例:
>> X = [1 0 4 -3 0 0 0 8 6]; find(X)
ans =
1 3 4 8 9
>> X = [1 0 4 -3 0 0 0 8 6]; find(X == 4)
ans =
3
程序:round( )
功能:round(X) 将 X 的每个元素四舍五入为最近的整数。在对等情况下,即有元素的小数部分恰为 0.5 时,round 函数会偏离零四舍五入到具有更大幅值的整数。round(X,N) 四舍五入到 N 位小数:
示例:
>> X = [2.11 3.5; -3.5 0.78]; Y = round(X)
Y =
2 4
-4 1
>> Y = round(pi,3)
Y =
3.1420
程序:max( );min( )
功能:通常用法1、A1=max(B) 若B为向量,则返回最大值;若为矩阵,则返回每列最大值;2、[A1 A2]=max(B) 若B为向量,则返回【最大值 索引下标】;若B为矩阵,则返回【每列最大值(向量) 每个最大值对应的行号(向量)】
示例:
>> [x y] = max([2 3 5 21 5 2])
x =
21
y =
4
>> [x y]= max([2 3 5 ;21 5 2])
x =
21 5 5
y =
2 2 1
程序: fseek()
功 能: 重定位流上的文件指针
用 法: int fseek(FILE *stream, long offset, int fromwhere);
描 述: 函数设置文件指针stream的位置。如果执行成功,stream将指向以fromwhere为基准,偏移offset个字节的位置。如果执行失败(比如offset超过文件自身大小),则不改变stream指向的位置。
文件中的起始位置,指定为字符向量、字符串标量或数值标量。
| 设置参数 | 功能描述 |
|---|---|
| ‘bof’ 或 -1 | 文件的开头 |
| ‘cof’ 或 0 | 文件中的当前位置 |
| ‘eof’ 或 1 | 文件的结尾 |
数据类型: double | char | string
程序:reshape( )
功能:reshape(A,sz1,…,szN) 将 A 重构为一个 sz1×…×szN 数组,其中 sz1,…,szN 指示每个维度的大小。
示例:
%% 将向量重构为矩阵
>> A = 1:10; B = reshape(A,[5,2])
B =
1 6
2 7
3 8
4 9
5 10
%% 将多维数组重构成矩阵
>> A = zeros(3,2,3)
A(:,:,1) =
0 0
0 0
0 0
A(:,:,2) =
0 0
0 0
0 0
A(:,:,3) =
0 0
0 0
0 0
>> B = reshape(A,9,2)
B =
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
程序:angle( )
功能: 为复数数组 Z 的每个元素返回相位角(以弧度为单位)。此角度介于 ±π 之间。
算法:angle 函数采用复数 z = x + iy 并计算 atan2(y,x),以求出 xy 平面上在 x 轴正方向与从原点到点 (x,y) 的射线之间形成的角度。此相位角也是复数对数的虚部,因为
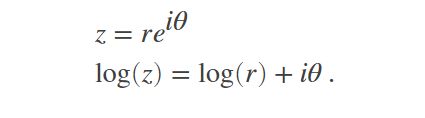
%% 创建复数值矩阵并计算每个元素的相位角。
>> Z = [1 - 1i 2 + 1i 3 - 1i 4 + 1i;
1 + 2i 2 - 2i 3 + 2i 4 - 2i]
Z =
1 至 2 列
1.0000 - 1.0000i 2.0000 + 1.0000i
1.0000 + 2.0000i 2.0000 - 2.0000i
3 至 4 列
3.0000 - 1.0000i 4.0000 + 1.0000i
3.0000 + 2.0000i 4.0000 - 2.0000i
>> P = angle(Z)
P =
-0.7854 0.4636 -0.3218 0.2450
1.1071 -0.7854 0.5880 -0.4636
程序:diff ( )
功能:相邻元素之间的差分;
-
如果 X 是长度为 m 的向量,则 Y = diff(X) 返回长度为 m-1 的向量。Y 的元素是 X 相邻元素之间的差分。
Y = [X(2)-X(1) X(3)-X(2) … X(m)-X(m-1)] -
如果 X 是不为空的非向量 p×m 矩阵,则 Y = diff(X) 返回大小为 (p-1)×m 的矩阵,其元素是 X 的行之间的差分。
Y = [X(2,:)-X(1,:); X(3,:)-X(2,:); … X(p,:)-X(p-1,:)]
如果 X 是 0×0 的空矩阵,则 Y = diff(X) 返回 0×0 的空矩阵。
示例:
%% 创建一个向量,然后计算相邻元素之间的一阶差分。
>> X = [1 1 2 3 5 8 13 21]; Y = diff(X)
Y =
0 1 1 2 3 5 8
%% 创建一个 3×3 矩阵,然后计算各列之间的一阶差分。
>> X = [1 1 1; 5 5 5; 25 25 25];
X =
1 1 1
5 5 5
25 25 25
>> Y = diff(X)
Y =
4 4 4
20 20 20
程序:mean ( )
功能:求数组的均值
- 如果 A 是向量,则 mean(A) 返回元素均值。
- 如果 A 为矩阵,那么 mean(A) 返回包含每列均值的行向量。
示例:
>> X = [1 1 1; 5 5 5; 25 25 25];
X =
1 1 1
5 5 5
25 25 25
>> Y = mean(X)
Y =
10.3333 10.3333 10.3333
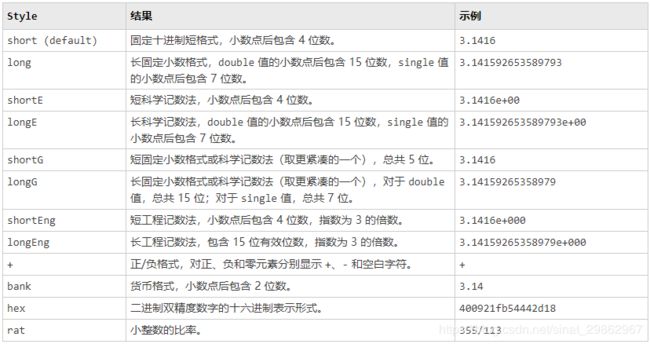
程序:format
功能:设置命令行窗口输出显示格式;format style 将命令行窗口中的输出显示格式更改为 style 指定的格式。
示例:
format long
pi
ans =
3.141592653589793