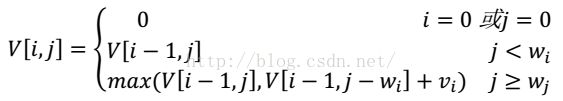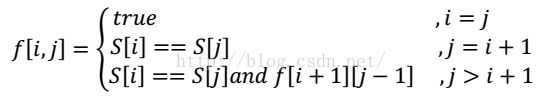算法学习—动态规划

动态规划（dynamic programming）是通过组合子问题来求解原问题的方法，它倾向于解决子问题重叠的情况，即不同子问题具有公共的子问题。

从这方面来看，动态规划都可以用递归来实现，但是递归是从上到下的思路进行处理的，也就是说递归是从完整的问题，逐次向子问题求解的过程，但是动态规划却是从规模最小的子问题开始，向上逐步求解，求解过程中保存这些小规模的子问题作为求解大问题的依据，并最终求出结果。例如求解斐波那契数列，使用递归的思路是从f(n)依次向下求解f(n-1)和f(n-2)，但是使用动态规划的思路是先求解f(0)和f(1)，然后依次向上求解f(2)，f(3) … f(n)。由此可以看出递归会重复（毕竟每次递归求f(n-1)和f(n-2)时都会求解依次f(n-3)，f(n-4) … f(0)）很多次，而动态规划只会求解一次。

通常动态规划可以按照如下四个步骤进行设计：
  1.刻画一个最优解的结构特征；
  2.递归地定义最优解的值；
  3.计算最优解的值，通常采用自底向上的方法；
  4.利用计算出的信息构造一个最优解（按照要求，可有可无）。

动态规划问题的解决很大程度上依赖于刻画出这个最优解的结构特征，并递归地构造出这个最优解，这个最优解的结构特征又可以用状态来描述，这个状态可以是个数组或者变量，用这个状态来描述计算的中间过程，从而达到计算出最终结果的目的。

矩阵链乘法-算法导论

给定n个矩阵的链，矩阵Ai的规模为Pi-1*Pi（1<=i<=n），求完全括号花方案，使得计算乘积A1A2…An所需的乘法次数最少。

1.最优括号化方案的结构特征

对于矩阵序列AiAi+1…Aj，我们假设分割点为k，将矩阵序列分为Ai..k和Ak+1..j，然后再计算它们的最终结果Ai..j。此方案的计算代价等于矩阵Ai..k的计算代价，加上矩阵Ak+1..j的计算代价，再加上两者相乘的计算代价。

2.一个递归的解决方案

令m[i, j]表示计算矩阵Ai..j所需标量乘法次数的最小值，那么原问题的最优解为，计算A1..n的最低代价，即m[1, n]。由于假设分割点为k，故AiAi+1..An的最小括号化方案的递归求解公式为：

这里的m[i, j]就是状态，表示Ai..j的最小代价的括号方案。

3.计算最优代价

void matrix_chain_order(const std::vector &p, 
			std::vector > &m, 
			std::vector > &r)
{
	int len = p.size() - 1;

	for(int i = 1;i <= len; i++){//[i,i]的代价为0
		m[i][i] = 0;
	}

	for(int l = 2; l <= len; l++){//每个切割出来的链的长度
		for(int i = 1; i <= len-l+1; i++){//m[i,j]中的i
			int j = i + l - 1;//m[i,j]中的j
			m[i][j] = INT_MAX;
			for(int k = i; k <= j-1; k++){//在[i..j]之间，依次分割成两部分，使得k为[i..j-1]
				int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];//计算出每次分割之后的代价
				if(q < m[i][j]){//检查和已经计算出的代价相比，是否更小
					m[i][j] = q;
					r[i][j] = k;//记录这段分割的分割点，r记录了每段的最优分割点
				}
			}
		}
	}
}

最大子段和-leetCode

在一个序列中寻找相邻的子数组，使得这个子数组的和最大。例如序列[−2, 1, −3, 4, −1, 2, 1, −5, 4]的最大子数组是[4, −1, 2, 1]，其和为6。

1.最优解的结构特征

对于序列AiAi+1..Aj，我们假定i到j之间的能够形成最大连续的子序列，那么我们遇到Aj+1是否可以将它并入已求得的最大连续子序列呢，这首先要看Ai..j的和是否大于零，如果大于零，那么可以认为包含Aj+1元素的最大字段为Ai..j+1，否则就只认为包含Aj+1元素的最大字段为Aj+1这一个元素。

2.递归的解决方案

令状态f[i]为包含元素A[i]，且以A[i]为最后一个元素的最大连续子序列的和。那么f[i]来自两种情况，一种是f[i-1]>0的情况，其值应该是f[i-1]+Ai，另一种是f[i-1]<=0，其值为Ai。

3.计算最优代价

int max_sublist_sum(std::vector &list){//按照表达式的代码
	std::vector b(list.size(), 0);
	int max = list[0];
	b[0] = list[0];
	for(int i = 1; i < list.size(); i++){
		if(b[i-1] <= 0) b[i] = list[i];
		else b[i] = b[i-1] + list[i];
		if(b[i] > max) max = b[i];
	}
	for(int i = 0; i < b.size(); i++) std::cout << b[i] <<" ";
	std::cout << std::endl;
	return max;
}
int max_sublist_sum_useone(std::vector &list){//修改为只是用一个变量的代码
	int max = list[0],b = list[0];
	for(int i = 1; i < list.size(); i++){
		if(b <= 0) b = list[i];
		else b = b + list[i];
		if(b > max) max = b;
	}
	return max;
}

最长公共子序列-算法导论

给定两个序列X=和Y=，求X和Y长度最长的公共子序列。注意，这里的最长公共子序列可以是不连续的，例如，ABCBDAB和BDCABA的最长公共子序列为BCBA，长度为4。

1.刻画最长公共子序列的特征

令X=和Y=为两个序列，Z=为X和Y的任意最长公共子序列，那么：
如果xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列
如果xm!=yn，则zk!=xm意味着Z是Xm-1和Y的最长公共子序列
如果xm!=yn，则zk!=yn意味着Z是X和Yn-1的最长公共子序列

2.递归的解决方案

令状态c[i, j]为Xi和Yj的最长公共子序列长度，那么当i=0或j=0时c[i, j]=0。根据以上描述的最长公共子序列的特征可以得出：

3.计算最优代价

int longest_common_subsequence_recursion(const std::string &x, const std::string y, int m, int n){
	if(m < 0 || n < 0) return 0;
	if(x[m] == y[n]){
		//std::cout << x[m] << std::endl;
		return longest_common_subsequence_recursion(x, y, m-1, n-1)+1;
	} else {
		return std::max(longest_common_subsequence_recursion(x, y, m-1, n),longest_common_subsequence_recursion(x, y, m, n-1));
	}
}
int longest_common_subsequence(const std::string &x, const std::string y){
	int m = x.length(), n = y.length();
	std::vector > b(m+1, std::vector(n+1));
	for(int i = 0; i <= m; i++){//注意多出来这一行表示空字符串时的情况
		b[i][0] = 0;
	}
	for(int i = 0; i <= n; i++){
		b[0][i] = 0;
	}
	for(int i = 0 ; i < m; i++){
		for(int j = 0 ; j < n; j++){
			if(x[i] == y[j]){
				b[i+1][j+1] = b[i][j] + 1;//这里给b的下标统一加了1
			} else {//x[i] != y[j]
				b[i+1][j+1] = std::max(b[i+1][j], b[i][j+1]);
			}
		}
	}
	return b[m][n];
}

最长回文子序列

回文是正序和逆序相同的非空字符串。这里的最长回文子序列和最长公共子序列一样，也不要求序列的连续性，只要是能够构成回文的非连续序列就称为一个回文子序列。例如，character的最长回文子序列为carac。

1.刻画最长回文子序列的特征

对于序列AiAi+1..Aj，那么 1）如果i和j相等，那么只有一个元素，它的长度就为1，并且是一个回文串；2）如果Ai和Aj相等，那么序列Ai..j中的回文串必定是序列Ai-1..j-1中的回文串长度加1；3）如果Ai和Aj不相等，那么Ai..j的回文串必定和Ai..j-1或者Ai+1..j的回文串长度相同（取较大那个）。

2.递归的解决方案

令状态L[i, j]为序列AiAi+1..Aj的最长回文串长度，那么根据以上描述，可以得出：

3.计算最优代价

int longest_palindrome_sublist(std::string &list){
	int len = list.length();
	std::vector > c(len, std::vector(len));

	for(int i = 0; i < len; i++){
		c[i][i] = 1;
	}
	for(int j = 1; j < len; j++){
		for(int i = j-1; i >= 0; i--){
			if(list[i] == list[j]){
				if(i+1 > j-1) c[i][j] = 2;
				else c[i][j] = c[i+1][j-1] + 2;
			} else {
				c[i][j] = std::max(c[i+1][j],c[i][j-1]);
			}
		}
	}

	return c[0][len-1];
}
int longest_palindrome_sublist_recursion(std::string &list, int low, int high){
	if(low > high){
		return 0;
	}
	if(low == high){
		return 1;
	}
	if(list[low] == list[high]){
		return longest_palindrome_sublist_recursion(list, low+1, high-1)+2;
	} else {
		return std::max(longest_palindrome_sublist_recursion(list, low, high-1),
						longest_palindrome_sublist_recursion(list, low+1, high));
	}
}

编辑距离-leetCode

为了将一个文本串A[0..mi]转换为目标串B[1..n]，我们可以使用多种变换操作，编辑距离的目标是寻找从A转化为B的最少操作。

这些操作包括三种形式：插入一个字符；删除一个字符；替换一个字符。

例如，abcd和abecd的编辑距离为1，因为可以删除abecd中的e（abecd->abcd）；也可在abcd中插入一个e（abcd->abecd）；也可以用c替换为e，d替换为c，再插入一个d，（abcd->abecd）此时编辑距离为3。但是要求的是最小编辑距离，故结果为1。

1.刻画编辑距离的特征

对于序列A1A2..Ai和序列B1B2..Bj，如果Ai和Bj相等，那么序列A1..i和B1..j的编辑距离与A1..i-1和B1..j-1的编辑距离是相等的；如果Ai和Bj不相等，那么有六种方式可以将A1..i转化为B1..j：

  a.将Ai替换成Bj，或者将Bj替换成Ai——此时的编辑距离为A1..i-1和B1..j-1的编辑距离+1
  b.在Ai后面添加一个Bj，或者删除B1..j中的Bj——此时的编辑距离为A1..i和B1..j-1的编辑距离+1
  c.将A1..i中的Ai删除，或者在Bj后面添加一个Ai——此时的编辑距离为A1..i-1和B1..j的编辑距离+1

2.递归的解决方案

令状态m[i][j]为A[0, i]和B[0, j]之间的最小编辑距离，那么按照以上描述，可以得出：

3.计算最优代价

int edit_distance_int_min_value(int t1, int t2, int t3){
	return (t1 < t2 ? t1 : t2 < t3 ? t2 : t3);
}
int edit_distance_recursion(std::string &s1, int start1, int end1, std::string &s2, int start2, int end2){

	if(start1 > end1){//其中有个到了结尾
		if(start2 > end2){//第二个也到了结尾
			return 0;
		} else {//没到结尾，剩下的长度就是我们要的
			return end2-start2+1;
		}
	}
	if(start2 > end2){//其中有个到了结尾
		if(start1 > end1){//第二个也到了结尾
			return 0;
		} else {//没到结尾，剩下的长度就是我们要的
			return end1-start1+1;
		}
	}
	if(s1[start1] == s2[start2]){
		return edit_distance_recursion(s1, start1+1, end1, s2, start2+1, end2);//相等
	} else {//s1[start1] != s2[start2]
		int t1 = edit_distance_recursion(s1, start1+1, end1, s2, start2, end2);//s1删除或者s2增加
		int t2 = edit_distance_recursion(s1, start1, end1, s2, start2+1, end2);//s1增加或者s2删除
		int t3 = edit_distance_recursion(s1, start1+1, end1, s2, start2+1, end2);//修改
		return edit_distance_int_min_value(t1, t2, t3)+1;
	}
}
int edit_distance(std::string &s1, int start1, int end1, std::string &s2, int start2, int end2){
	std::vector > m(s1.length()+1,std::vector(s2.length()+1));

	for(int i = 0 ; i <= s1.length();i++){//初始状态需要注意下，相当于空串和另外一个串的编辑距离
		m[i][0] = i;
	}
	for(int i = 0 ; i <= s2.length();i++){
		m[0][i] = i;
	}
	for(int i = 1 ; i <= s1.length(); i++){
		for(int j = 1; j <= s2.length(); j++){
			if(s1[i-1] == s2[j-1]){
				m[i][j] = m[i-1][j-1];
			} else {
				//修改、s1删除或者s2增加、s1增加或者s2删除
				m[i][j] = edit_distance_int_min_value( m[i-1][j-1], m[i-1][j], m[i][j-1] )+1;
			}
		}
	}
	return m[s1.length()][s2.length()];
}

Best Time to Buy and Sell Stock III-leetCode

数组A[i]表示第i天的股票价格，设计算法找出通过买进和卖出能够得到的最大利润。注意，最多只能进行两次买进和卖出。

1.刻画问题的特征

对于任意一天i，它之前的这段时间内能获取最大的利润（包括i当天），加上它之后的这段时间能获取的最大利润（包括i当天），就是这段时间总共能获取的最大利润。

2.递归的解决方案

令状态f(i)表示[0..i](0 ≤ i ≤ n-1)的最大利润，状态g(i)表示区间[i..n-1](0 ≤ i ≤ n-1)的最大利润，则总共的最大利润为max{f(i)+g(i)},0 ≤ i ≤ n-1。当i=0时，f(i)=0,i=n-1时，g(i)=0。

3.计算最优代价

int maxProfit(std::vector& prices) {
	if (prices.size() < 2) return 0;
	const int n = prices.size();
	std::vector f(n, 0);
	std::vector g(n, 0);
	for (int i = 1, valley = prices[0]; i < n; ++i) {
		valley = std::min(valley, prices[i]);
		f[i] = std::max(f[i - 1], prices[i] - valley);
	}
	for (int i = n - 2, peak = prices[n - 1]; i >= 0; --i) {
		peak = std::max(peak, prices[i]);
		g[i] = std::max(g[i], peak - prices[i]);
	}
	int max_profit = 0;
	for (int i = 0; i < n; ++i)
		max_profit = std::max(max_profit, f[i] + g[i]);
	return max_profit;
}

Palindrome Partitioning II-leetCode

给定一个字符串s，将s分割为一系列子串，这些子串均为回文串。例如s=”aab”，则分割数为1，应该分割为[“aa”,”b”]。

1.分析

定义状态 f(i, j) 表示区间 [i, j] 之间最小的 cut 数，则状态转移方程为

这是一个二维函数，实际写代码比较麻烦。
所以要转换成一维DP。如果每次，从i往右扫描，每找到一个回文就算一次DP的话，就可以转换为f(i)=区间 [i, n-1] 之间最小的cut数，n为字符串长度，则状态转移方程为

一个问题出现了，就是如何判断 [i, j] 是否是回文？每次都从 i 到 j 比较一遍？太浪费了，这里也是一个DP问题。
定义状态 P[i][j] = true if [i, j] 为回文，那么 P[i][j] = str[i] == str[j] && P[i+1][j-1]

2.计算最优代价

int palindrome_partitioning(std::string s){
	int len = s.length();
	std::vector > isPalindrome(len,std::vector(len));
	std::vector f(len + 1);

	for(int i = 0; i <= len; i++){
		f[i] = len-i-1;
	}

	for(int i = len-1; i >=0; i--){
		for(int j = i; j < len; j++){
			if(s[i] == s[j] && (j-i < 2 || isPalindrome[i+1][j-1])){
				isPalindrome[i][j] = true;
				f[i] = std::min(f[j+1]+1, f[i]);
			}
		}
	}

	return f[0];
}

0-1背包问题-算法设计技巧与分析

有n个商品，第i个商品价值vi美元，重wi磅，vi和wi都是整数，有一个背包，能容纳C磅重的商品，求取价值最大的装法。注，物品不能分割。

例如，V=[60, 100, 120]，W=[10, 20, 30]，C=50，那么价值最大的装法为220=100+120。

1.分析
设V[i, j](0≤i≤n,0≤j≤C)表示从前i项{u1,u2,..,ui}中取出来的装入体积为j的背包的物品的最大价值。对于V[0, j]表示没有商品，故值为0，对于V[i, 0]表示背包空间为0，故值也为0。另外的情况：a. j

2.计算最优代价

int knapsack(std::vector &p,std::vector &w, int C){
	int n = p.size();
	std::vector > V(n+1, std::vector(C+1));

	for(int i = 0; i <= n; i++){
		V[i][0]=  0;
	}
	for(int i = 0; i <= C; i++){
		V[0][i]=  0;
	}
	for(int i = 1; i <= n;i++){
		for(int j = 1; j <= C; j++){
			V[i][j] = V[i-1][j];
			if(w[i-1] <= j){
				V[i][j] = std::max(V[i][j], V[i-1][j-w[i-1]]+p[i-1]);
			}
		}
	}
	return V[n][C];
}

Longest Palindromic Substring -leetCode

从字符串S中截取出来一个最长的回文子串（连续的串）。

1.分析

取状态为f(i, j)，表示区间[i, j]是否是回文串，那么有三种情况，假设i到j之间，只有一个字符，那么肯定是回文串，如果有两个字符，那么就要判断它们是否相等，相等的话也是回文串，如果有多于两个的字符，除了要判断S[i] == S[j]外，还要判断它们包含的字符串是不是回文串，那么状态转移方程为：

2.计算最优代价

string LongestPalindromicSubstring(string &str){
	int len = str.length();
	vector > f(len, vector(len, 0));
	size_t max_start = 0, max_len = 0;
	for(size_t i = 0; i < len; i++){
		f[i][i] = 1;
		for(size_t j = 0; j < i; j++){
			f[j][i] = (str[i] == str[j] && (i-j < 2 || f[j+1][i-1]));
			if(f[j][i] && (i - j + 1) > max_len){
				max_start = j;
				max_len = i - j + 1;
			}
		}
	}
	return str.substr(max_start, max_len);
}