图论4之图的最小生成树及拓扑排序
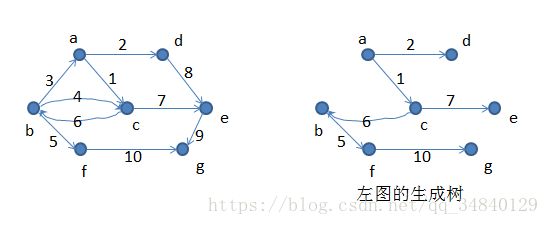
生成树
![]()
同一个连通图可以有不同的生成树。例如对于图9-1(a),其余3个子图都是它的生成树。在每棵生成树中都包含8个顶点和7条边,即n个顶点和n-1条边,此时n等于原图中的顶点数8,它们的差别只是边的选取方法不同。
在这3棵生成树中,图9-1(b)中的边集是从图9-1(a)中的顶点V0出发,利用深度优先搜索遍历的方法而得到的边集,此图是原图的深度优先生成树;图9-1(c)中的边集是从图9-1(a)中的顶点V0出发,利用广度优先搜索遍历的方法而得到的边集,此图是原图的广度优先生成树;图9-1(d)是原图的任意一棵生成树。当然图9-1(a)的生成树远不止这3种,只要能连通所有顶点而又不产生回路的任何子图都是它的生成树。
生成树: 如果连通图G的一个子图是一棵包含G的所有顶点的树,则该子图称为G的生成树。
生成树是连通图的包含图中的所有顶点的极小连通子图。它并不唯一,从不同的顶点出发进行遍历,可以得到不同的生成树。
其中,权值最小的树就是最小生成树。
关于最小生成树最经典的应用模型就是城市通信线路网最小造价的问题:网络G表示n个城市之间的通信线路(其中顶点表示城市,边表示两个城市之间的通信线路,边上的权值表示线路的长度或造价),通过求该网络的最小生成树找到求解通信线路总造价最小的最佳方案。
求图的最小生成树主要有两种经典算法:
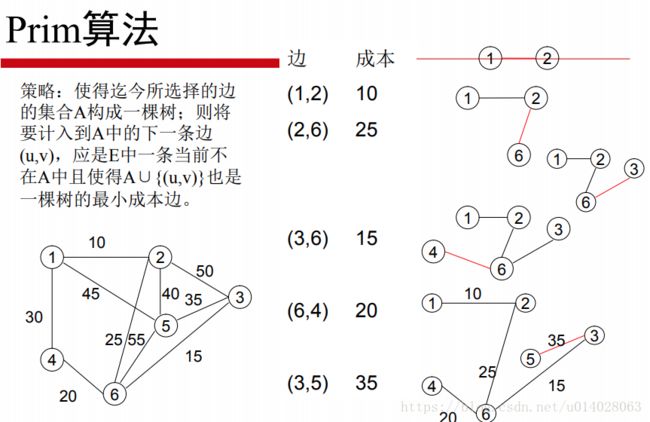
1,普里姆(Prim)算法 时间复杂度为O(n2),适合于求边稠密的最小生成树。
2,克鲁斯卡尔(Kruskal)算法
一、Prim算法
1.概览
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
2.算法简单描述
取图中任意一个顶点V作为生成树的根,之后若要往生成树上添加顶点W,则在顶点V和W之间必定存在一条边。并且该边的权值在所有连通顶点V和W之间的边中取值最小。
下面对算法的图例描述
| 图例 | 说明 | 不可选 | 可选 | 已选(Vnew) |
|---|---|---|---|---|
|
|
此为原始的加权连通图。每条边一侧的数字代表其权值。 | - | - | - |
|
|
顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点,因此将A及对应边AD以高亮表示。 | C, G | A, B, E, F | D |
|
|
下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F与相应边DF以高亮表示。 | C, G | B, E, F | A, D |
| 算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。 | C | B, E, G | A, D, F | |
|
|
在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。E最近,因此将顶点E与相应边BE高亮表示。 | 无 | C, E, G | A, D, F, B |
|
|
这里,可供选择的顶点只有C和G。C距E为5,G距E为9,故选取C,并与边EC一同高亮表示。 | 无 | C, G | A, D, F, B, E |
|
|
顶点G是唯一剩下的顶点,它距F为11,距E为9,E最近,故高亮表示G及相应边EG。 | 无 | G | A, D, F, B, E, C |
|
|
现在,所有顶点均已被选取,图中绿色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39。 | 无 | 无 | A, D, F, B, E, C, G |
3.简单证明prim算法
反证法:假设prim生成的不是最小生成树
1).设prim生成的树为G0
2).假设存在Gmin使得cost(Gmin)
3).将
4).这与prim每次生成最短边矛盾
5).故假设不成立,命题得证.
4.时间复杂度
这里记顶点数v,边数e
邻接矩阵:O(v2) 邻接表:O(elog2v)
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Prim算法
"""
def prim(graph, vertex_num):
INF = 1 << 10
visit = [False] * vertex_num
dist = [INF] * vertex_num
#preIndex = [0] * vertex_num
#对所有的顶点进行循环,首先是确定头结点
#找到当前无向图的最小生成树
for i in range(vertex_num):
minDist = INF + 1
nextIndex = -1
#第一次循环时,nextIndex就是头结点
#所以要把minDIst加上1,之后这个循环
#的功能是找到基于当前i,邻接矩阵中i行到哪一行距离最小的那个位置作为下一个结点,当然前提是那个结点没有去过
for j in range(vertex_num):
if dist[j] < minDist and not visit[j]:
minDist = dist[j]
nextIndex = j
print (nextIndex)
visit[nextIndex] = True
#由于前面已经找到了下一个结点了,现在就要构建再下一个结点的dist矩阵了,这就要看当前这个nextIndex这一行了
for j in range(vertex_num):
if dist[j] > graph[nextIndex][j] and not visit[j]:
dist[j] = graph[nextIndex][j]
#preIndex[j] = nextIndex
return dist, #preIndex
if __name__ == '__main__':
_ = 1 << 10 # init inf
graph = [
[0, 6, 3, _, _, _],
[6, 0, 2, 5, _, _],
[3, 2, 0, 3, 4, _],
[_, 5, 3, 0, 2, 3],
[_, _, 4, 2, 0, 5],
[_, _, _, 3, 5, 0],
]
prim(graph, 6)二、Kruskal算法
1.概览
Kruskal算法是一种用来寻找最小生成树的算法,由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是,Kruskal算法在图中存在相同权值的边时也有效。
2.算法简单描述
1).记Graph中有v个顶点,e个边
2).新建图Graphnew,Graphnew中拥有原图中相同的e个顶点,但没有边
3).将原图Graph中所有e个边按权值从小到大排序
4).循环:从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中
if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中
添加这条边到图Graphnew中
图例描述:
![]() 首先第一步,我们有一张图Graph,有若干点和边
首先第一步,我们有一张图Graph,有若干点和边
![]()
将所有的边的长度排序,用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序,对局部最优的资源进行选择,排序完成后,我们率先选择了边AD。这样我们的图就变成了右图
![]() 在剩下的变中寻找。我们找到了CE。这里边的权重也是5
在剩下的变中寻找。我们找到了CE。这里边的权重也是5
![]() 依次类推我们找到了6,7,7,即DF,AB,BE。
依次类推我们找到了6,7,7,即DF,AB,BE。
![]()
下面继续选择, BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了(对于BC可以通过CE,EB来连接,类似的EF可以通过EB,BA,AD,DF来接连)。所以不需要选择他们。类似的BD也已经连通了(这里上图的连通线用红色表示了)。
最后就剩下EG和FG了。当然我们选择了EG。最后成功的图就是右:
3.简单证明Kruskal算法
对图的顶点数n做归纳,证明Kruskal算法对任意n阶图适用。
归纳基础:
n=1,显然能够找到最小生成树。
归纳过程:
假设Kruskal算法对n≤k阶图适用,那么,在k+1阶图G中,我们把最短边的两个端点a和b做一个合并操作,即把u与v合为一个点v',把原来接在u和v的边都接到v'上去,这样就能够得到一个k阶图G'(u,v的合并是k+1少一条边),G'最小生成树T'可以用Kruskal算法得到。
我们证明T'+{
用反证法,如果T'+{
由数学归纳法,Kruskal算法得证。
时间复杂度:elog2e e为图中的边数
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
__mtime__ = '2018/10/22'
"""
tinyEWG_txt = """
{
0:[(6,0.58),(2,0.26),(4,0.38),(7,0.16)],
1:[(3,0.29),(2,0.36),(7,0.19),(5,0.32)],
2:[(6,0.40),(7,0.34),(1,0.36),(0,0.26),(3,0.17)],
3:[(6,0.52),(1,0.29),(2,0.17)],
4:[(6,0.93),(0,0.38),(7,0.37),(5,0.35)],
5:[(1,0.32),(7,0.28),(4,0.35)],
6:[(4,0.93),(0,0.58),(3,0.52),(2,0.40)],
7:[(2,0.34),(1,0.19),(0,0.16),(5,0.28)]
}
"""
## 模拟优先队列
class Min_PQ_:
def __init__(self, f, reversed=False):
self.data = []
self.f = f
self.__reversed = reversed
def remove(self):
return self.data.pop(0)
def insert(self, item):
self.data.append(item)
self.data.sort(key=self.f, reverse=self.__reversed)
def __len__(self):
return len(self.data)
def __str__(self):
return str(self.data)
# 补全edge
def fill(g):
for v in g:
for i in range(0, len(g[v])):
g[v][i] = (v,) + g[v][i]
def mst_prim(g):
visited = set()
pq = Min_PQ_(lambda x: x[-1])
mst = []
def visit(v):
visited.add(v)
for edge in g.get(v, []):
pq.insert(edge)
visit(0)
while pq:
min_edge = pq.remove()
x, y = min_edge[0], min_edge[1]
if x in visited and y in visited:
continue
else:
mst.append(min_edge)
if x not in visited: visit(x)
if y not in visited: visit(y)
return mst
def get_edges_set(g):
s = set()
for v in g:
for e in g.get(v, []):
a, b, weight = e[0], e[1], e[-1]
if a < b:
s.add((a, b, weight))
else:
s.add((b, a, weight))
return s
def add_edge(g, x, y):
if x in g:
(g[x]).append(y)
else:
g[x] = []
add_edge(g, x, y)
def has_connected(g, x, y):
has_connected__ = False
visited = set()
def __dfs(__x):
visited.add(__x)
for v in g.get(__x, []):
if v == y:
nonlocal has_connected__
has_connected__ = True
return
elif v not in visited:
__dfs(v)
__dfs(x)
return has_connected__
def mst_kruskal(g):
sorted_edges = list(get_edges_set(g))
sorted_edges.sort(key=lambda x: x[-1])
mst = []
g_temp = dict()
while sorted_edges:
min_edge = sorted_edges.pop(0)
x, y = min_edge[0], min_edge[1]
if has_connected(g_temp, x, y):
continue
else:
mst.append(min_edge)
add_edge(g_temp, x, y)
add_edge(g_temp, y, x)
return mst
if __name__ == '__main__':
g = eval(tinyEWG_txt)
fill(g)
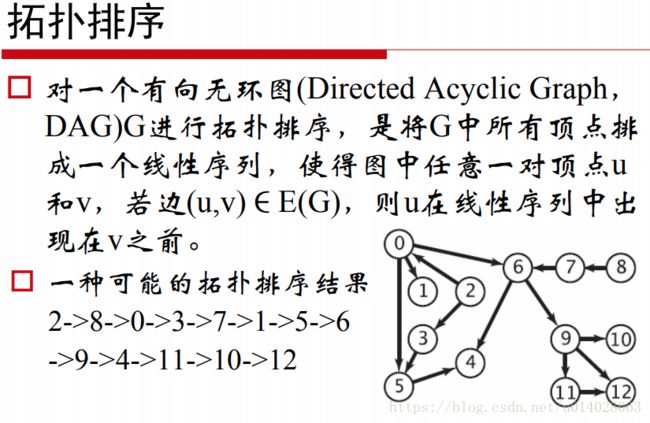
print(mst_kruskal(g))三、拓扑排序
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
拓扑排序
"""
def indegree0(v, e):
if v == []:
return None
tmp = v[:]
for i in e:
if i[1] in tmp:
tmp.remove(i[1])
if tmp == []:
return -1
for t in tmp:
for i in range(len(e)):
if t in e[i]:
e[i] = 'toDel' # 占位,之后删掉
if e:
eset = set(e)
eset.remove('toDel')
e[:] = list(eset)
if v:
for t in tmp:
v.remove(t)
return tmp
def topoSort(v, e):
result = []
while True:
nodes = indegree0(v, e)
if nodes == None:
break
if nodes == -1:
print('there\'s a circle.')
return None
result.extend(nodes)
return result
if __name__ == '__main__':
v = ['a', 'b', 'c', 'd', 'e']
e = [('a', 'b'), ('a', 'd'), ('b', 'c'), ('d', 'c'), ('d', 'e'), ('e', 'c')]
res = topoSort(v, e)
print(res)