分层图最短路问题,就是把一个图分层然后跑最短路(废话)。
分层图最短路问题关键在于怎么分层,分层通常是起到对题中某个条件的限定作用,这里我们结合例题看看。
Luogu P4568飞行路线
题意大致是给一个带权无向图,允许k次飞行费用为0,求最小费用。
这里就是将图分成k层,每次从第i-1层到第i层相当于是走了一条免费的飞行路线。然后如果从第i层回到第i-1层就是一个“后悔”的过程。因此建图方法就是每层之间正常连边,层与层之间上到下边权为0,下到上正常边权。这样直接跑Dijkstra就好了。这里分层就是对k次免费进行限制,而且连反向的边保证程序有反悔的机会。
搬运一个大佬题解里的图。
#include
#include
#include
#include
#include
#define N 1000010
#define M 5000010
using namespace std;
int head[N],nxt[M],to[M],val[M];
int n,m,cnt;
void Add(int u,int v,int w)
{
nxt[++cnt] = head[u];
head[u] = cnt;
to[cnt] = v;
val[cnt] = w;
return;
}
int k,s,t;
int dis[N];
struct qwq
{
int u,dis;
bool operator < (const qwq &a) const
{
return dis > a.dis;
}
}top,node;
priority_queueq;
const int inf = 100000010;
bool vis[N];
void dijkstra()
{
for(int i = 0;i <= n + k * n;i++) dis[i] = inf;
dis[s] = 0;
top.u = s;
top.dis = 0;
q.push(top);
while(q.size())
{
top = q.top();
q.pop();
int u = top.u;
if(!vis[u])
{
vis[u] = 1;
for(int i = head[u];i;i = nxt[i])
{
int v = to[i];
if(dis[v] > dis[u] + val[i])
{
dis[v] = dis[u] + val[i];
node.u = v,node.dis = dis[v];
q.push(node);
}
}
}
}
}
int main()
{
scanf("%d %d %d",&n,&m,&k);
scanf("%d %d",&s,&t);
for(int i = 1;i <= m;i++)
{
int u,v,w;
scanf("%d %d %d",&u,&v,&w);
Add(u,v,w);
Add(v,u,w);
for(int i = 1;i <= k;i++)
{
Add(u + (i - 1) * n,v + i * n,0);
Add(v + i * n,u + i * n,w);
Add(v + (i - 1) * n,u + i * n,0);
Add(u + i * n,v + i * n,w);
}
}
for(int j = 1;j <= k;j++)
{
Add(t + (j - 1) * n,t + j * n,0);
}
dijkstra();
printf("%d",dis[t + k * n]);
return 0;
}
Luogu P1073最优贸易
题意要求我们从一个点买入,一个点卖出,获得的费用最大,并且从1能到达n。
emmmm这个题题解里有很多玄学做法,这里只讨论分层图做法。我们暴力的想一想,每一个点都有可能买入,每一个点都有可能卖出,但是必须先买入再卖出(显然的嘛)。所以这其实就存在一个依赖关系。这样就可以将图分成3层,第一层表示没有买入和卖出,第二层表示已经买入,第三层表示已经卖出。那么每层内部正常连边(边权为0),层与层之间,第一层到第二层要连边权为-a[u](u为第一层内边的起点,a[u]为费用)表示买入,第二层到第三层连边权为a[u]的边表示卖出。而第二层第三层回不到第一层就是我们限制了贸易次数,只进行一次贸易。这样图就建好了。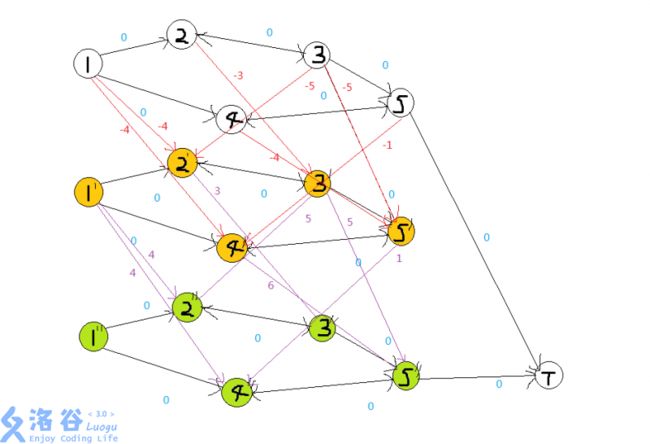
仍然搬运大佬题解的图。
#include
#include
#include
#include
#include
#include
#include
#include<set>
#include
#include
#include<string>
using namespace std;
#define P system("pause");
#define A(x) cout << #x << " " << (x) << endl;
#define AA(x,y) cout << #x << " " << (x) << " " << #y << " " << (y) << endl;
#define ll long long
#define inf 1000000000
#define linf 10000000000000000
#define mem(x) memset(x,0,sizeof(x))
int read()
{
int x = 0,f = 1;
char c = getchar();
while(c < '0' || c > '9')
{
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
{
x = (x << 3) + (x << 1) + c - '0';
c = getchar();
}
return f * x;
}
#define N 300100
#define M 3000010
int head[N],nxt[M],to[M],val[M],dis[N],vis[N],a[N];
int n,m,cnt;
void add(int u,int v,int w)
{
nxt[++cnt] = head[u];
head[u] = cnt;
to[cnt] = v;
val[cnt] = w;
return;
}
void Add(int u,int v)
{
add(u,v,0);
add(u + n,v + n,0);
add(u + 2 * n,v + 2 * n,0);
add(u,v + n,-a[u]);
add(u + n,v + 2 * n,a[u]);
}
int s,t;
void spfa()
{
queue<int>q;
q.push(s);
for(int i = 1;i <= t;i++)
{
dis[i] = -inf;
}
vis[s] = 1;
dis[s] = 0;
while(!q.empty())
{
int u = q.front();
q.pop();
vis[u] = 0;
for(int i = head[u];i;i = nxt[i])
{
int v = to[i];
if(dis[v] < dis[u] + val[i])
{
dis[v] = dis[u] + val[i];
if(!vis[v])
{
vis[v] = 1;
q.push(v);
}
}
}
}
return;
}
int main()
{
n = read(),m = read();
s = 1,t = 3 * n + 1;
for(int i = 1;i <= n;i++) a[i] = read();
for(int i = 1;i <= m;i++)
{
int u = read(),v = read(),z = read();
Add(u,v);
if(z == 2) Add(v,u);
}
add(n,t,0);
add(3 * n,t,0);
spfa();
printf("%d\n",dis[t]);
}
总结一下,分层图最短路通常是按照题中的限制关系进行分层,通过层与层间的连通与否,边权进行限制,从而实现在跑最短路时也能兼顾限制条件。同时由于最短路算法是枚举点进行松弛,无法保证一次就得到最优解,因此往往通过一些方法实现“反悔”操作,例题1就是通过回到原来的层实现的,而例题2则是通过spfa不断松弛实现的。
