数组及字符串题目大杂烩

数组及字符串类型的题目花式很多，涉及到很多技巧，什么双指针、滑动窗口、单调栈、分治、二分、动态规划。而且有的题目存在很多变体，比如字符串类题目中的回文串类的题目，看着大同小异，做起来往往容易犯难，因此有必要做个笔记记录一下解题思路。由于套路繁多，因此个人认为用“大杂烩”来代替“整理”作为标题更为贴切。当然，这是一项大工程，慢慢记录当做复习了！希望复习之后能在看到类似题目就映射到对应的技巧进而想到代码实现，哈哈，估计不可能。

数组

盛最多水的容器（中等）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/container-with-most-water
给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

思路：这个题用双指针法。左右两端各设置一个指针，左侧指针只能右移，右侧指针只能左移。计算容积，之后移动指向较短边的指针，后再次计算容积，如此循环。在每次计算时都要与当前的返回值作比较，如果更大了就替换成新值，第一次计算则跟初始值（0）比较。
双指针法实现很简单，而且该方法是对暴力法的极大简化，暴力法要枚举所有可能的情况。那么双指针方法会不会有所遗漏呢？答案是不会。这里就拿题目中的实例进行说明。

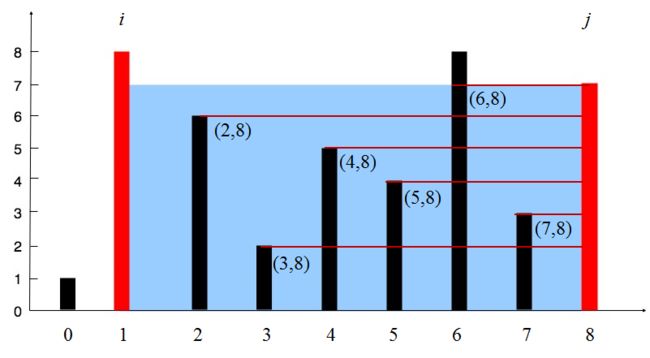
这种情况下显然是 j 要向左移动，这样一来相对暴力枚举而言，(2,8),(3,8),…,(7,8)这几种情况的计算显然都省去了。这种省去是合理的，首先这几种情况的底的长显然显然是比(1,8)的要短的，而且算容积又只看短的边，因此这几种情况下容器的有效高度不会超过7，也就是 j 指向的边的长。所以这几种情况下容器的容积都要小于7×(8-1)。同时，这也说明了为什么每次要移动短的边，因为移动长的边不可能得到比当前情况更优的情况，而移动短的边则有可能遇到，虽然底缩短了，但万一遇到长的边呢，还是有机会超过先前的最大值的。而且由于每次移动，省略掉的都是不如当前状态的情况，因此不会漏下最优解。

C++代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1;
        int res = 0;
        while(i < j){
            int area;
            if(height[i] > height[j]){
                area = height[j] * (j-i);
                --j;
            }
            else{
                area = height[i] * (j-i);
                ++i;
            }
            res = max(res,area);
        }
        return res;
    }
};

柱状图中最大的矩形（困难）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

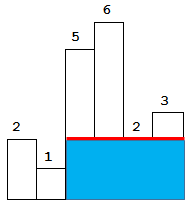
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

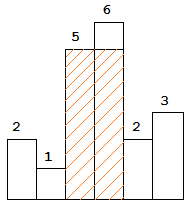
思路：这道题乍一看和上面一题很像，然而有细微差别，这细微差别导致了在解题思路上的不同。这题对于情况(i,j)，其面积取决于i到j之间（包括二者）最短的柱子。为此我们换个思路解题，类似于使用回文串题目中的中心扩展法，对于一个柱子，就向两边扩展，当某一边遇到比该柱子短的柱子的时候就停下，这样我们就找到了该柱子所能“撑起”的最大面积。例如下面左数第五根柱子，其所能撑起的最大面积为2×4=8，再大就大不了了，因为左右都过不去了。

我们顺序遍历每一根柱子，得到每个柱子所能“撑起”的最大面积，其中的最大值就是题目所要求的解。由此，则题目转化为求每个柱子所能撑起了最大面积的左边界及右边界的问题。我们用单调栈来解决这一问题。其实个人认为单调栈只是一个结果，并不是有意要维护这个单调栈，只是因为要找某个元素左（右）侧第一个比它小的元素的位置，所以用上的栈数据结构进行辅助，为了找第一个比它小的元素的位置，肯定是要把栈中比它大的元素的位置给弹出的，所以这个栈正好就构成了单调栈，并且单调递增。

C++代码1：
这个代码为了易读直观而牺牲在性能上有所牺牲。其实分别找寻左右首个比当前元素小的元素的位置，只要遍历一遍就够了。因为在出栈时，对于出栈的元素来说，其右侧首个比其所指元素小的元素的位置，就是当前遍历到的位置。对此在后面给出简便的代码，但其实时间复杂度是一样的。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> left(n);//记录某位置元素左侧的第一个比它小的元素的位置
        vector<int> right(n);//记录某位置元素右侧的第一个比它小的元素的位置
        stack<int> s1;
        stack<int> s2;
        s1.push(-1);
        s2.push(n);
        for(int i = 0; i < n; ++i){
            while(s1.top()!=-1 && heights[s1.top()]>=heights[i]){
                s1.pop();
            }
            left[i] = s1.top();
            s1.push(i);
        }
        for(int i = n-1; i >= 0; --i){
            while(s2.top()!=n && heights[s2.top()]>=heights[i]){
                s2.pop();
            }
            right[i] = s2.top();
            s2.push(i);
        }
        int res = 0;
        for(int i = 0; i < n; ++i){
            res = max(res, (right[i]-left[i]-1)*heights[i]);
        }
        return res;
    }
};

C++代码2：
方法还是单调栈，就是代码简化了一下，也没简化太多。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();   
        int res = 0;  
        stack<int> S;
        S.push(-1);
        for (int i = 0; i < n; ++i) {
            while (S.top()!=-1 && heights[S.top()] >= heights[i]) {
                int tmp = heights[S.top()];
                S.pop();
                res = max(res, tmp*(i-S.top()-1));
            }
            S.push(i);
        }
        
        while(S.top()!=-1) {
            int tmp = heights[S.top()];
            S.pop();
            res = max(res, tmp*(n-S.top()-1));
        }
        return res;
    }
};

注：个人认为单调栈、双指针这样的“技巧”和深度优先搜索、动态规划这样的“方法”还是有些不同的。单调栈、双指针之类的题目，读题后不好想出解题的这些技巧，但想到了就很好做。深度优先搜索、动态规划的题目，方法很好想到，但就是写不出题解，有时候只能硬套方法。（哈哈（假），哭（真））

四数之和（中等）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/4sum
给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

注意：

答案中不可以包含重复的四元组。

示例：

给定数组 nums = [1, 0, -1, 0, -2, 2]，和 target = 0。

满足要求的四元组集合为：
[
  [-1,  0, 0, 1],
  [-2, -1, 1, 2],
  [-2,  0, 0, 2]
]

思路：这个题目和它的几个同伴（两数之和，三数之和）差不多，用双指针都可以解决，但是在代码的复杂性上有些提高。解题思路很简单，先用个sort排序，之后循环遍历前两个数，后面两个数用前后双指针的方式寻找。为了避免重复，遇到相同的数就直接跳过。

C++代码：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());
        vector<vector<int>> res;
        int N = nums.size();
        for(int i = 0; i < N; ++i){
            if(i>0&&nums[i-1]==nums[i])
                continue;
            for(int j = i + 1; j < N; ++j){
                if(j>i+1&&nums[j-1]==nums[j])
                    continue;
                int l = N - 1;
                int t = target-nums[i]-nums[j];
                for(int k = j + 1; k < N; ++k){
                    if(k>j+1&&nums[k-1]==nums[k])
                        continue;
                    while(k < l && nums[k]+nums[l]>t){
                        --l;
                    }
                    if(k==l) break;
                    if(nums[k]+nums[l] == t){
                        res.push_back({nums[i],nums[j],nums[k],nums[l]});
                    }
                }
            }
        }
        return res;
    }
};

注：按照上述思路写代码没什么烧脑的，无非就是繁琐，做题最重要的还是心态，要是一直提交一直有问题，心态崩了，那就不好了。

分割数组的最大值（困难）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/split-array-largest-sum
给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。

注意:
数组长度 n 满足以下条件:

1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)
示例:

输入:
nums = [7,2,5,10,8]
m = 2

输出:
18

解释:
一共有四种方法将nums分割为2个子数组。
其中最好的方式是将其分为[7,2,5] 和 [10,8]，
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

思路：如果说上面一个题纯考编码而没什么技巧性，那么这个题就有比较强的技巧性了，想到了编码就很容易。这个题当然可以用动态规划来做，但我觉得二分搜索在理解上以及在编码上更友好一些。我们可以观察到解是不可能比数组中的最大值小的，同时又不可能大于数组全体元素的和。由于题目又要求每一段连续（如果不要求连续我就不会做了），因此我们可以应用二分搜索的方法。二分搜索的左边界是left = max{nums[0], nums[1], ... ,nums[n]}，右边界是right = sum{nums[0], nums[1], ... ,nums[n]}。求个mid = (left + right)/2，然后循环遍历数组，同时维护一个计数器count和分段和sub，如果和超过mid，计数器加1。到最后比较count和题目规定的分段数m的大小。如果count小了就表示mid太大，数组不够分，反之则mid太小，导致分段过多。最终能找到一个合适的值。

C++代码：

class Solution {
public:
    int splitArray(vector<int>& nums, int m) {
        long left = 0, right = 0;
        for(auto num:nums){
            left = left>num?left:num;
            right += num;
        }
        while(left < right){
            long mid = (left + right)/2;
            long sub = 0;//维持一个和
            int count = 1;//计数
            for(auto num:nums){
                sub += num;
                if(sub > mid){
                    ++count;
                    sub = num;
                }
            }
            if(count > m){
                left = mid + 1;
            }
            else {
                right = mid;
            }
        }
        return left;
    }
};

注：编码很简单，前提是要想到二分搜索啊！

（剑指）数组中的逆序对（困难）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

思路：这个题很好，还能复习一下归并排序，没错，这个题目就是用到归并排序的思想，只不过在归并排序merge的过程中增加了一个求逆序对的过程。怎么求？用下图的例子来说明。
下面序列的左半边与右半边都已经排序完成，二者自己的逆序对数量已经求完了。现在进行merge，求二者间的逆序对。在merge的过程中，由于1<2，因此i右移至3处，此时3>2，就要计算逆序对。显然，由于上下两个序列都已经完成了merge的过程，因此二者自己都是有序的，所以3后面的数肯定比2大，由此可得逆序对为3，即mid-i+1。之后2被放到归并排序创建的临时数组中，j右移，此时就相当于右侧数组中的2对左侧数组的逆序对数量已经求完了。merge完成后，左侧与右侧数组间的逆序对数量已经得到，此时再加上左侧数组的逆序对数量及右侧数组的逆序对数量，就是整个数组的逆序对数量。左侧数组的逆序对数量和右侧数组的逆序对数量数量怎么求？归并排序中用到的分治。
对于归并排序，我在排序算法概念梳理及C++实现笔记中进行了记录。

C++代码：

class Solution {
    int mergesort(vector<int>& nums, vector<int>& vec, int l, int r){
        if(l == r){
            return 0;
        }
        int mid = (l + r)/2;
        int left = mergesort(nums, vec, l, mid);
        int right = mergesort(nums, vec, mid + 1, r);
        int i = l, j = mid + 1, k = l;
        int count = 0;
        while(i <= mid && j <= r){
            if(nums[i] > nums[j]){
                vec[k++] = nums[j++];
                count += (mid - i + 1);
            }
            else{
                vec[k++] = nums[i++];                
            }
        }
        if(i <= mid) copy(nums.begin() + i, nums.begin() + mid + 1, vec.begin() + k);
        if(j <= r) copy(nums.begin() + j, nums.begin() + r + 1, vec.begin() + k);
        copy(vec.begin() + l, vec.begin() + r + 1, nums.begin() + l);
        return left + right + count; 
    }
public:
    int reversePairs(vector<int>& nums) {
        int n = nums.size();
        if(n == 0) return 0;
        vector<int> vec(n);
        return mergesort(nums, vec, 0, n - 1);
    }
};

字符串

最长回文子串（中等）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-palindromic-substring
给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

思路：这是一道经典题目，可用的方法有很多，个人最爱中心扩展法，在理解上最为清晰。另外回文串类的题目有不少用这种方法，因此值得学习。当然，还可以用动态规划做。另外，也可以用Manacher算法，这个算法太复杂了，虽然改善了时间复杂度，但是提高了思考复杂度，以脑力换时间（哭了）。

中心扩展，就是从中心往两边扩展，比较两边是字符是否相同，相同就再扩展。另外要注意子串长度可能为奇数也可能为偶数，当子串长度为偶数的时候中心就不是具体的字符了。顺序遍历每个中心，计算每个中心对应的最长回文子串的长度，最终找出整个字符串中的最长回文子串。

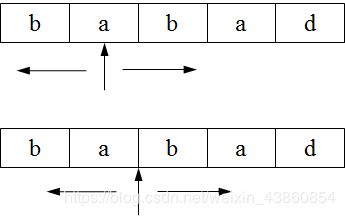
中心扩展法C++代码：
这个代码为了直观而牺牲了简洁性，一般可以把中心扩展的过程写成一个函数。

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        int start = 0, len = 1;//初始化起点和长度
        //偶数长度子串
        for(int i = 0; i < n; ++i){
            int left = i, right = i + 1;
            while(left>=0 && right<n && s[left]==s[right]){
                --left;
                ++right;
            }
            if(right-left-1 > len){
                len = right-left-1;
                start = left + 1;
            }
        }
        //奇数长度子串
        for(int i = 0; i < n; ++i){
            int left = i, right = i;
            while(left>=0 && right<n && s[left]==s[right]){
                --left;
                ++right;
            }
            if(right-left-1 > len){
                len = right-left-1;
                start = left + 1;
            }
        }
        return s.substr(start, len);
    }
};

回文子串（中等）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/palindromic-substrings
给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被计为是不同的子串。

示例 1:

输入: "abc"
输出: 3
解释: 三个回文子串: "a", "b", "c".

示例 2:

输入: "aaa"
输出: 6
说明: 6个回文子串: "a", "a", "a", "aa", "aa", "aaa".

注意:
输入的字符串长度不会超过1000。

思路：同上题，这个题目也可以用中心扩展法做。

中心扩展法C++代码：
这里我把中心扩展的过程写成了一个函数。

class Solution {
public:
    int fun(string &s, int left, int right){
        int count = 0;
        while(left>=0 && right<s.size() && s[left]==s[right]){
            --left;
            ++right;
            ++count;
        }
        return count;
    }
    int countSubstrings(string s) {
        int n = s.size();
        int res = 0;
        for(int i = 0; i < n; ++i){
            int num1 = fun(s, i, i);
            int num2 = fun(s, i, i+1);
            res += (num1 + num2);
        }
        return res;
    }
};

注：回文串的一连串题目后面继续做几个笔记，感觉比较有意思。

最小覆盖子串（困难）(还没写题解，还在思考)

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-window-substring
给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字符的最小子串。

示例：

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"

说明：

如果 S 中不存这样的子串，则返回空字符串 “”。
如果 S 中存在这样的子串，我们保证它是唯一的答案。