原
分治算法详解（超详细）
分治算法详解
一、基本概念
在计算机科学中，分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……
任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小，越容易直接求解，解题所需的计算时间也越少。例如，对于n个元素的排序问题，当n=1时，不需任何计算。n=2时，只要作一次比较即可排好序。n=3时只要作3次比较即可，…。而当n较大时，问题就不那么容易处理了。要想直接解决一个规模较大的问题，有时是相当困难的.
二、基本思想及策略
分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。
分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
如果原问题可分割成k个子问题，1
三、分治法适用的情况
分治法所能解决的问题一般具有以下几个特征：
1) 该问题的规模缩小到一定的程度就可以容易地解决
2) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解；
4) 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。
第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；
第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；、
第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。
第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。
四、分治法的基本步骤
分治法在每一层递归上都有三个步骤：
step1 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
step2 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
step3 合并：将各个子问题的解合并为原问题的解。
它的一般的算法设计模式如下：
Divide-and-Conquer(P)
1. if |P|≤n0
2. then return(ADHOC(P))
3. 将P分解为较小的子问题 P1 ,P2 ,...,Pk
4. for i←1 to k
5. do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi
6. T ← MERGE(y1,y2,...,yk) △ 合并子问题
7. return(T)
其中|P|表示问题P的规模；n0为一阈值，表示当问题P的规模不超过n0时，问题已容易直接解出，不必再继续分解。ADHOC(P)是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC(P)求解。算法MERGE(y1,y2,...,yk)是该分治法中的合并子算法，用于将P的子问题P1 ,P2 ,...,Pk的相应的解y1,y2,...,yk合并为P的解。
五、分治法的复杂性分析
一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：
T（n）= k T(n/m)+f(n)
通过迭代法求得方程的解：
递归方程及其解只给出n等于m的方幂时T(n)的值，但是如果认为T(n)足够平滑，那么由n等于m的方幂时T(n)的值可以估计T(n)的增长速度。通常假定T(n)是单调上升的，从而当 mi≤n
六、可使用分治法求解的一些经典问题
（1）二分搜索
（2）大整数乘法
（3）Strassen矩阵乘法
（4）棋盘覆盖
（5）合并排序
（6）快速排序
（7）线性时间选择
（8）最接近点对问题
（9）循环赛日程表
（10）汉诺塔
七、依据分治法设计程序时的思维过程
实际上就是类似于数学归纳法，找到解决本问题的求解方程公式，然后根据方程公式设计递归程序。
1、一定是先找到最小问题规模时的求解方法
2、然后考虑随着问题规模增大时的求解方法
3、找到求解的递归函数式后（各种规模或因子），设计递归程序即可。
八、下面我对分治法的一些程序适当的演示！
1：对于大数问题的思考(1)
下面采用分治法的逻辑看看是否可行，在这里我们举例 3的2000次方，由于整形最多20亿，毋庸置疑这里已经超过了界限！为了方便说明是否可以分治 以及如何分治，请看这样一个算式：
123 345 678 * 3 = 370 037 034
在这里我们可以这样写：
123 * 3 = 369
345 * 3 = 1035
678 * 3 = 2034 组合在一起是
369 1035 2034。
看到这个结果，与原结果相比较，你发现了什么？其实早就在古代我们的老祖宗就发明了算盘的这个计算工具，回想一下他的计算方式，逢10进1，也就是我们通常所说的10进制表示法！
在这里，我们可以想得到 1000进制吧，也就是逢1000往上位进1，那么每个位上最大的也只能是999，而没有1000了。 利用这个思想，我们来看看上面的算式！
369 1035 2034
369+1 035+2 034
（加1，得370） （进1，保留037） （进2，保留034）
那么最后的结果也就是 370 037 034 发现结果刚好一样，这就是我们所谓的1000进表示法
值得说明一下：为何1000进制表示出来的数和10进制表示出来的数是一样的，其实不仅如此，100进制 1000进制 乃至10000进制，表示的最后结果都是一样的，不知道你发现了没？
举个例子：10进制的199，用100进制表示也是1 99,10进制的1099 用1000进制表示也是 1 099（注意这个0不能略去）以此类推！
好了，回到正题，上面那个算式通过拆分为3个数的思想，这就体现了分治法的思想，
首先他满足第一条件：分解到一定小规模的时候可以解决
第二条件：每个小规模都具有最佳子结构（在变量范围内，可以用来表示）
第三条件：每个小问题可以通过合并在一起形成大问题的解
第四条件：每个小问题相互独立
这几点他都满足了，当然可以利用分治思想了！接下来看我们的题目 3的2000次方，在这里我们采用10000进制数组表示法！！该函数源码如下：
-
void RandomBigNumFun(int low,int high) //传递参数为底数和指数
-
{
-
-
unsigned
int temp[
1024] = {
0};
//初始化一个数组，用来存放10000进制的数据
-
temp [
0] = low;
//初始化第一个元素为需要的值！
-
int flag =
-1;
//标记变量，用来指示是否需要往上一位进位，同事保存进多少
-
unsigned
int m_count =
1;
//技术变量，计算数组中被占用了多少个元素
-
int _index,index;
//两个循环变量
-
-
for(_index =
0;_index
-1; ++_index)
//循环high-1次 因为本身temp[0]= low，
-
{
-
for(index =
0; index < m_count ; ++index)
//循环m_count次，其实原本可以把整个数组循环完
-
{
//只不过耗时了，因为实际有值的地方只有m_count个
-
temp[ index ] *= low;
-
-
if(flag !=
-1)
//检测下一位是否溢出，需要向自己进位
-
{
-
temp[index] += flag;
-
flag =
-1;
//进位之后别忘记把标记在设置为-1
-
}
-
-
if(temp[index] >
9999)
//判断是否需要向上一位进位
-
{
-
flag = temp[index]/
10000 ;
-
temp[index] %=
10000;
-
}
-
}
-
-
if(flag !=
-1)
-
{
-
temp[index] += flag;
-
++m_count;
-
flag =
-1;
-
}
-
-
if(m_count >
1023)
-
{
-
printf(
"数据过大而数组过小，请重置存放数组的大小");
-
exit(
0);
-
}
-
}
-
-
for(index = m_count
-1;index >=
0;--index)
//这里值得说明，如果该位上是1，则要输出0001，因为是一万进制
-
{
-
if(temp[index] <
10)
-
cout<<
"000"<
-
else
if(temp[index] <
100)
-
cout<<
"00"<
-
else
if(temp[index] <
1000)
-
cout<<
"0"<
-
else
-
cout<
-
}
-
-
}
其实上述函数需要传递参数进去，这里就传3和2000进去，运行结果如下(大得难以想象)：
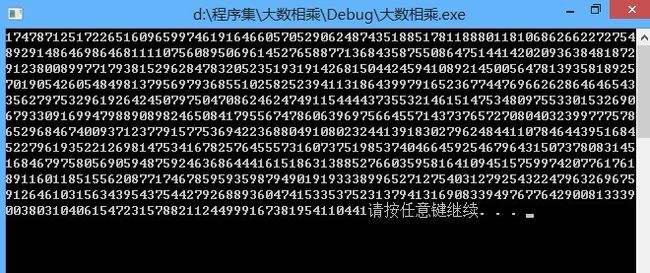如有不懂的地方，欢迎在我的博客留言！！
对于大数问题的思考(2):
上述所讲是大数的乘方形式出现，接下来演示大数相乘的计算方法，例如：27392361983108271361039746313 乘以 37261038163103818366341087632113
呵呵，当然在这里我不会写这么大一个数组，我只会举一个简单的例子 如 234 * 456 = ？？？？
有人可能会问：博主，这样的直接计算就可以算出来，还需要分治吗？ 在这里我主要讲一种通用的算法思想，那么无论遇见多大的数字，都可以这样来写！
算法前的分析：在这里我们若把456拆分为4,5,6，然后分别去乘以234，结果是什么样勒？答案如下：
234
x 456
____________________
1404
1170
936
------------------------------------
106704
这样的结构大家都清楚，可是我们需要怎么用程序来保留这个结果勒，不妨设一个二维数组来保存结果，数组的第一行保留1404，第二行保留1170，第三行保留936，
由于不能直接存储，我们需要对存放的位置做一下计算：数组该有多少行，该有多少列？
在这里我们需要知道，两个三位数的乘积，结果最多为6位数，一个2位一个6位相乘，结果最多为2+6=8位，所以这里数组该有6列，而对于行数，则由被乘数决定，所以这里为3行！！、
temp [3] [6] = {
0 0 1 4 0 4
0 1 1 7 0 0
0 9 3 6 0 0
}
每列依次往下加 1 0 6 7 0 4;所得刚好为我们要的答案，好了，废话不多说，这里直接看代码！！
-
#include
-
using
namespace
std;
-
-
inline int Translate(char str)
-
{
-
return (str -
48);
-
}
-
-
int _tmain(
int argc, _TCHAR* argv[])
-
{
-
char NumStr1 [
3] = {
'2',
'3',
'4'};
-
char NumStr2 [
3] = {
'4',
'5',
'6'};
-
int temp[
3][
6] = {
0};
-
signed
int flag =
-1;
-
-
int Temp_x =
0;
-
int Temp_y ;
-
-
int _index,index;
-
-
for(_index =
2;_index >=
0 ;--_index)
//这里的两重循环是分别赋值到二维数组里面
-
{
-
Temp_y =
5 - Temp_x;
-
-
for(index =
2;index >=
0;--index,--Temp_y)
-
{
-
temp[Temp_x][Temp_y] = Translate(NumStr2[_index]) * Translate(NumStr1[index]);
-
-
if(flag !=
-1)
-
{
-
temp[Temp_x][Temp_y] += flag;
-
flag =
-1;
-
}
-
-
if(temp[Temp_x][Temp_y] >=
10)
-
{
-
flag = temp[Temp_x][Temp_y]/
10;
-
temp[Temp_x][Temp_y] %=
10;
-
}
-
}
-
-
if(flag !=
-1)
-
{
-
temp[Temp_x][Temp_y] += flag;
-
flag =
-1;
-
}
-
++ Temp_x;
-
}
-
-
-
int temp_sum[
6]={
0};
-
flag =
-1;
-
-
for(
int j=
5;j >=
0;-- j)
//接下来这个循环是加每一列的数组到最后的结果数组里面
-
{
-
for(
int i=
2;i>=
0;--i)
-
temp_sum[j] += temp[i][j];
-
if(flag !=
-1)
-
{
-
temp_sum[j] += flag;
-
flag =
-1;
-
}
-
-
if( temp_sum[j] >=
10)
-
{
-
flag = temp_sum[j] /
10;
-
temp_sum[j] %=
10;
-
}
-
}
-
-
flag =
-1;
-
-
for(
int i =
0;i !=
6;++ i)
//这里是输出结果
-
-
cout<
-
cout<<
endl;
-
system(
"pause");
-
return
0;
-
}
运行结果如下所示：
所得结果跟我们预想的一样 ，但是这个程序有个小bug，因为两个三位数相乘，不一定是6位数，也许是5位数，所以输出的时候记得判断下第一个是否为0！
看到这里，读者可以自己改编以上程序为一个函数，求任意两个数字的乘积，只是那样的话需要动态创建数组了！
2：递归与分治的结合（汉诺塔问题）
关于递归，他也可看做是属于分治思想的一种体现，递归问题到处可见，可他始终是一个重难点，在这里我主要说一下递归中的汉诺塔这个经典的问题！
至于什么是汉诺塔，如果有不知道的可以百度，在这里我不累述，直接在程序中说明：
-
#include
-
#include
-
-
static
int count =
-1;
-
-
void move(char x,char y);
// 对move函数的声明
-
void hanoi(int n,char one,char two,char three) ;
// 对hanoi函数的声明\
-
-
int main()
-
{
-
int m;
-
printf(
"请输入一共有多少个板子需要移动:");
-
scanf(
"%d",&m);
-
printf(
"以下是%d个板子的移动方案:\n",m);
-
hanoi(m,
'A',
'B',
'C');
-
system(
"pause");
-
return
0;
-
}
-
-
void hanoi(int n,char one,char two,char three) // 定义hanoi函数
-
// 将n个盘从one座借助two座,移到three座
-
{
-
-
if(n==
1)
-
move(one,three);
-
else
-
{
-
hanoi(n
-1,one,three,two);
//首先把n-1个从one移动到two
-
move(one,three);
//然后把最后一个n从one移动到three
-
hanoi(n
-1,two,one,three);
//最后再把n-1个从two移动到three
-
}
-
}
-
-
-
void move(char x,char y) // 定义move函数
-
{
-
count++;
-
if( !(count%
5) )
-
printf(
"\n");
-
printf(
"%c移动至%c ",x,y);
-
}
如果输入5个板子，则移动的方案为：
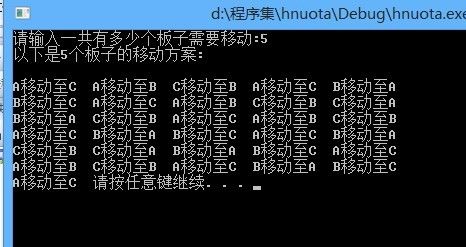结果所示便为移动过程，至于内部是怎么实现的，读者可自己下来画出示意图，便一目了然！！
2：二分搜索法(二分查找) ,利用分治思想缩小范围!
二分法的思想说来比较简单,就是利用上下限不停的缩小查找的界限,当缩小到一定范围内的时候,就可以解决,这个算法也十分常见,在这里我不在累述了
-
#include
-
using
namespace
std;
-
int binary_sreach(int *array,int len,int elem);
-
-
int main(int argc, char* argv[])
-
{
-
int a[
7] = {
1,
2,
3,
6,
8,
9,
99};
-
cout<
7,
6);
-
system(
"pause");
-
return
0;
-
}
-
-
int binary_sreach(int *array,int len,int elem)
-
{
-
int low =
0;
-
int high = len -
1;
-
int middle;
-
while (low <= high)
-
{
-
middle = (low + high)/
2;
-
if(
array[middle] == elem)
-
return middle;
-
-
else
if(
array[middle] > elem)
-
high = middle;
-
else
-
low = middle;
-
}
-
-
return
-1;
-
}
-
运行结果也可想而知是3，二分法其实也就这么简单，这里也明显利用了分治的思想！！
分治法是一个非常重要的算法思想，在各种程序设计大赛上经常采用分治思想解答，这里只是列举了一些经典问题的解法，具体问题还需要具体分析，以后我会持续更新，每次遇见就记录下来给大家分享！