Harmonious Army HDU2019多校赛第二场【网络流建图套路】

传送门

最近好像越来越懒了
也越来越忙了
所以就直接到处cpy
这不是你放弃高质量题解的理由啊喂
由于实在是没有时间，所以就先cpy一下 让自己先看懂

这是（官方）给出的题解
以下是某集训队论文

（考试的时候tly dalao tql快速翻出这篇论文 ->“套路题”->快速列方程->解一下 建个图 跑最小割=最大流就好了）
（%%%）

下面加入一些我自己的理解
假设我们先得到所有的收益
但显然这样的状态是不合法的 因为不能两个都选 是非黑即白的操作
题目中点分别向$s$和$t$连边
割可以表示一种状态
点被割到$s$集表示选$s$ 被割到$t$集表示选$t$
割掉这条边表示不选对应的选项
则会产生“损失”
要让损失最小 则跑最小割
具体说明一下那个方程的列法：

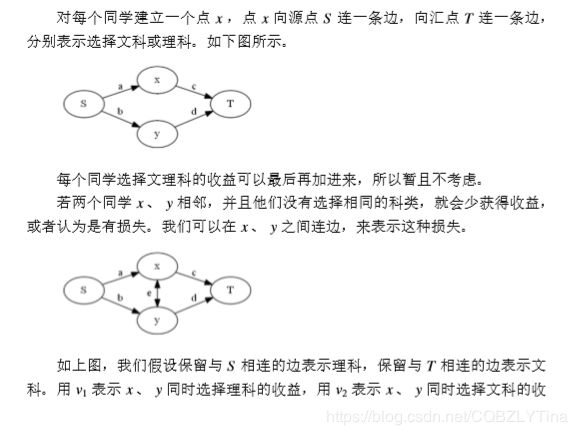
个人的收益先暂不考虑 $s$表示文科，$t$表示理科
1.都选文 割去$a$ $b$ 则$a$ $b$之和为两人都选理的收益
2.都选理 同理 割去$c$ $d$ 则$c$ $d$之和为两人都选文的收益
3.两人一文一理 割去$a$ $e$ $d$或$b$ $e$ $c$ 同理 他们之和为两人都选理的收益加上两人都选文的收益
分别令$a=b$ $c=d$ 解出方程组

---

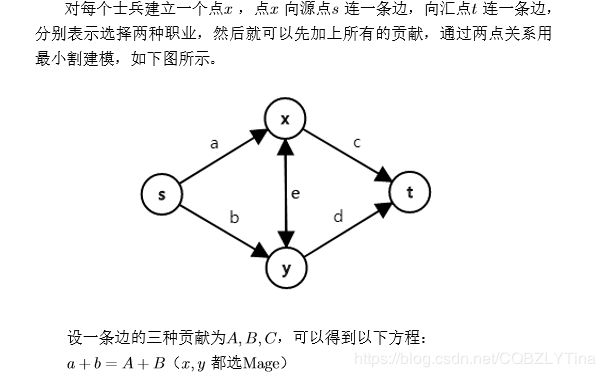
类比列出这道题的方程：（原来我还记得我在讲这道题

$s$表示Warriors，$t$表示Mage
$$a+b=A+B$$
$$c+d=B+C$$
$$a+e+d=A+C$$
$$b+e+c=A+C$$
把$B$换成$a/4+c/3$ 再令$a=b,c=d$（是不定方程，所以要限制一下）
把边解出来建图就可以了

---

两道例题：
happiness
就是论文里面的那道题

文理分科
这道题稍微有些不一样
它是一堆人一起选择某一个才会得到附加的收益
而之前的题是两个人
（其实用之前的套路应该是可以的 但是以下建图方法比较易懂 而且方便）
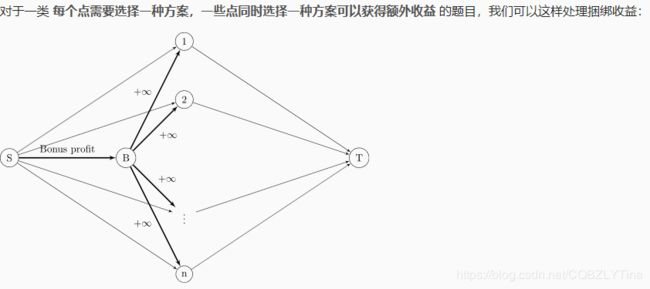
新建一个点 这个点连向$s$的权值为所有点都选$s$的额外收益
将新建的点，向相邻的那几个点中的每一个点（或从相邻的那几个点中的每一个点向新建的点）
连一条长度为inf的边，这样的边在最小割中肯定不会存在，
则保证了在代表共同选择收益的边不被割时（即都选一个科目）
新建的点与相邻的点在同一个点集

（图片来自某谷）

#include
#include
#include
#include
using namespace std;
#define MAXN 30005
#define MAXM 140005
//不会算大小qwq 
#define LL long long
#define INF 0x3f3f3f3f
int n,m,s,t;
int cur[MAXN];
int dis[MAXN]/*距离标号*/,gap[MAXN]/*距离标号为i的点的数量*/;
int mf;//maxflow
int cnt=1,head[MAXN];
struct node{
    int v,nxt,w;
}edge[MAXM*2];
void addedge(int u,int v,int w)
{
    edge[++cnt].v=v;
    edge[cnt].w=w;
    edge[cnt].nxt=head[u];
    head[u]=cnt;
}
void bfs()
{//初始化bfs 从t到s搜初始距离标号 
    memset(dis,-1,sizeof(dis));
    memset(gap,0,sizeof(gap));
    dis[t]=0,gap[0]=1;
    queue<int>Q;
    while(!Q.empty())
        Q.pop();
    Q.push(t);
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        for(int i=head[u];i;i=edge[i].nxt)
        {
            int v=edge[i].v;
            if(dis[v]!=-1) continue;//判重
            Q.push(v);
            dis[v]=dis[u]+1;
            gap[dis[v]]++;
        }
    }
    return ;
}
int dfs(int u,int f)
{
    if(u==t)
    {
        mf+=f;
        return f;
    }
    int used=0;//实际增广量 
    for(int i=head[u];i;i=edge[i].nxt)
    {
        cur[u]=i;
        int v=edge[i].v,w=edge[i].w;
        if(w&&dis[v]+1==dis[u])
        {
            int mi=dfs(v,min(w,f-used));
            if(mi)
            {
                edge[i].w-=mi;
                edge[i^1].w+=mi;
                used+=mi;
            }
            if(used==f) return used;//达到可增广上限 提前结束算法 
        }
        
    }
    gap[dis[u]]--;
    if(gap[dis[u]]==0) dis[s]=n+1;
    dis[u]++;
    gap[dis[u]]++;
    return used; 
}
int ISAP()
{
    mf=0;
    bfs();
    while(dis[s]<n)
    {
        memcpy(cur,head,sizeof(head));
        dfs(s,INF);
    }
    return mf;
}
int ans;
int main()
{
    scanf("%d %d",&n,&m);
    s=0,t=n*m+1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			int w;scanf("%d",&w);ans+=w;
			addedge(s,(i-1)*m+j,w);
			addedge((i-1)*m+j,s,0);
		}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			int w;scanf("%d",&w);ans+=w;
			addedge((i-1)*m+j,t,w);
			addedge(t,(i-1)*m+j,0);
		}
	//int cnt=n*m+1;//cnt重名 
	int num=n*m+1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			int w;scanf("%d",&w);ans+=w;
			num++;
			addedge(s,num,w);addedge(num,s,0);
			addedge(num,(i-1)*m+j,INF);addedge((i-1)*m+j,num,0);
			if(i-1>=1)
				addedge(num,(i-2)*m+j,INF),addedge((i-2)*m+j,num,0);
			if(i+1<=n)
				addedge(num,i*m+j,INF),addedge(i*m+j,num,0);
			if(j-1>=1)
				addedge(num,(i-1)*m+j-1,INF),addedge((i-1)*m+j-1,num,0);
			if(j+1<=m)
				addedge(num,(i-1)*m+j+1,INF),addedge((i-1)*m+j+1,num,0);
		}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			int w;scanf("%d",&w);ans+=w;
			num++;
			addedge(num,t,w);addedge(t,num,0);
			addedge((i-1)*m+j,num,INF);addedge(num,(i-1)*m+j,0);
			if(i-1>=1)
				addedge((i-2)*m+j,num,INF),addedge(num,(i-2)*m+j,0);
			if(i+1<=n)
				addedge(i*m+j,num,INF),addedge(num,i*m+j,0);
			if(j-1>=1)
				addedge((i-1)*m+j-1,num,INF),addedge(num,(i-1)*m+j-1,0);
			if(j+1<=m)
				addedge((i-1)*m+j+1,num,INF),addedge(num,(i-1)*m+j+1,0);
		}
	n=num+1;
	ans=ans-ISAP();
	printf("%d\n",ans);
    return 0;
}
/*
将新建的点，向相邻的那几个点中的每一个点
（或从相邻的那几个点中的每一个点向新建的点）连一条长度为inf
的边，这样的边在最小割中肯定不会存在，
则保证了在代表共同选择收益的边不被割时（即都选一个科目）
新建的点与相邻的点在同一个点集
*/

---

还是把这题的代码放一下吧 （我终于想起来自己是在讲哪道题了

#include
#include
#include
#include
using namespace std;
#define MAXN 505
#define MAXM MAXN*MAXN
#define LL long long
#define INF 0x3f3f3f3f
int n,m,s,t;
int cur[MAXN];
int dis[MAXN]/*距离标号*/,gap[MAXN]/*距离标号为i的点的数量*/;
LL mf;//maxflow
int cnt=1,head[MAXN];
struct node{
    int v,nxt;
    LL w;
}edge[MAXM*2];
void addedge(int u,int v,LL w)
{
    edge[++cnt].v=v;
    edge[cnt].w=w;
    edge[cnt].nxt=head[u];
    head[u]=cnt;
}
void bfs()
{//初始化bfs 从t到s搜初始距离标号 
    //memset(dis,-1,sizeof(dis));
    //memset(gap,0,sizeof(gap));
    dis[t]=0,gap[0]=1;
    queue<int>Q;
    while(!Q.empty())
        Q.pop();
    Q.push(t);
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        for(int i=head[u];i;i=edge[i].nxt)
        {
            int v=edge[i].v;
            if(dis[v]!=-1) continue;//判重
            Q.push(v);
            dis[v]=dis[u]+1;
            gap[dis[v]]++;
        }
    }
    return ;
}
LL dfs(int u,LL f)
{
    if(u==t)
    {
        mf+=f;
        return f;
    }
    LL used=0;//实际增广量 
    for(int i=head[u];i;i=edge[i].nxt)
    {
        cur[u]=i;
        int v=edge[i].v;LL w=edge[i].w;
        if(w&&dis[v]+1==dis[u])
        {
            LL mi=dfs(v,min(w,f-used));
            if(mi)
            {
                edge[i].w-=mi;
                edge[i^1].w+=mi;
                used+=mi;
            }
            if(used==f) return used;//达到可增广上限 提前结束算法 
        }
    }
    gap[dis[u]]--;
    if(gap[dis[u]]==0) dis[s]=n+1;
    dis[u]++;
    gap[dis[u]]++;
    return used; 
}
LL ISAP()
{
    mf=0;
    bfs();
    while(dis[s]<n)
    {
        memcpy(cur,head,sizeof(head));
        dfs(s,INF);
    }
    return mf;
}
LL ip[MAXN][2],ans;
int main()
{
    while(~scanf("%d %d",&n,&m))
    {
        cnt=1;
        s=0,t=n+1;ans=0;
        for(int i=0;i<=n+1;i++)
            ip[i][0]=0,ip[i][1]=0,head[i]=0,dis[i]=-1,gap[i]=0;
        for(int i=1;i<=m;i++)
        {
            int u,v,a,b,c;
            scanf("%d %d %d %d %d",&u,&v,&a,&b,&c);
            LL w=3*a+2*c;
            w=w*2;
            addedge(u,v,w);
            addedge(v,u,0);
            addedge(v,u,w);
            addedge(u,v,0);
            ip[u][0]+=3*a+16*c;ip[v][0]+=3*a+16*c;
            ip[u][1]+=15*a+4*c;ip[v][1]+=15*a+4*c;
            ans+=a+b+c;
        }
        for(int i=1;i<=n;i++)
            addedge(s,i,ip[i][0]),addedge(i,s,0),addedge(i,t,ip[i][1]),addedge(t,i,0);
        n+=2;
        ans=ans-ISAP()/24;
        printf("%lld\n",ans);
    }
    return 0;    
}