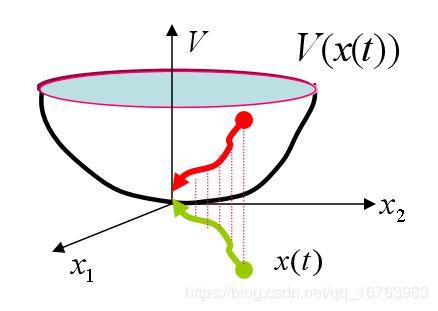
Lyapunov函数对微分方程稳定性的判别
Lyapunov函数(广义能量函数)稳定性判别定理
考虑系统 x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x),设 x e = 0 x_e=0 xe=0为一平衡点,如果存在连续可微的标量函数 V ( x ) V(x) V(x)满足:
(1) V ( x ) V(x) V(x)正定
(2) V ˙ = ∂ V ( x ) ∂ x f ( x ) \dot{V}=\frac{\partial V(x)}{\partial x}f(x) V˙=∂x∂V(x)f(x)半负定
则系统的平衡点 x e = 0 x_e=0 xe=0是Lyapunov稳定的。
Lyapunov函数渐进稳定性判别定理
考虑系统 x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x),设 x e = 0 x_e=0 xe=0为一平衡点,如果存在连续可微的标量函数 V ( x ) V(x) V(x)满足:
(1) V ( x ) V(x) V(x)正定
(2) V ˙ = ∂ V ( x ) ∂ x f ( x ) \dot{V}=\frac{\partial V(x)}{\partial x}f(x) V˙=∂x∂V(x)f(x)半负定
(3)集合{ x ∈ R n ∣ V ˙ ( x ) = 0 x\in R^n|\dot{V}(x)=0 x∈Rn∣V˙(x)=0}不包括系统的除平衡点以外的状态轨迹,则系统的平衡点 x e = 0 x_e=0 xe=0是Lyapunov渐进稳定的。
进一步,若 V ( x ) V(x) V(x)半径无穷大,则系统的平衡点 x e = 0 x_e=0 xe=0是Lyapunov全局渐进稳定的。
推论
考虑系统 x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x),设 x e = 0 x_e=0 xe=0为一平衡点,如果存在连续可微的标量函数 V ( x ) V(x) V(x)满足:
(1) V ( x ) V(x) V(x)正定
(2) V ˙ = ∂ V ( x ) ∂ x f ( x ) \dot{V}=\frac{\partial V(x)}{\partial x}f(x) V˙=∂x∂V(x)f(x)负定
则系统的平衡点 x e = 0 x_e=0 xe=0是Lyapunov渐进稳定的。
ps.判断稳定性是利用了线性代数中的二次型 正定矩阵等知识来定号
例题
1
求单摆在(0,0)处的稳定性

{ x 1 ˙ = x 2 x 2 ˙ = − g l s i n x 1 − k m x 2 \left\{ \begin{aligned} \dot{x_1} & = x_2\\ \dot{x_2} & = -\frac{g}{l}sinx_1-\frac{k}{m}x_2 \\ \end{aligned} \right. ⎩⎨⎧x1˙x2˙=x2=−lgsinx1−mkx2
选择V函数: V ( x ) = g l ( l − c o s x 1 ) + x 2 2 2 . V(x)= \frac{g}{l}(l-cosx_1)+\frac{x_2^2}{2}. V(x)=lg(l−cosx1)+2x22.
其中,
V ( x ) 正 定 V(x)正定 V(x)正定
V ˙ ( x ) = g l s i n x 1 x ˙ 1 + x 2 x ˙ 2 \dot{V}(x)=\frac{g}{l}sinx_1\dot{x}_1+x_2\dot{x}_2 V˙(x)=lgsinx1x˙1+x2x˙2
将 x ˙ 1 , x ˙ 2 \dot{x}_1,\dot{x}_2 x˙1,x˙2代入上式,
V ˙ ( x ) = − k m x 2 2 半 负 定 \dot{V}(x)=-\frac{k}{m}x_2^2半负定 V˙(x)=−mkx22半负定
∴ 单 摆 在 ( 0 , 0 ) 处 稳 定 \therefore 单摆在(0,0)处稳定 ∴单摆在(0,0)处稳定
2
已知系统方程如下,用Lyapunov函数判断稳定性
{ x 1 ˙ = x 2 − x 1 ( x 1 2 + x 2 2 ) x 2 ˙ = − x 1 − x 2 ( x 1 2 + x 2 2 ) \left\{ \begin{aligned} \dot{x_1} & = x_2-x_1(x_1^2+x_2^2)\\ \dot{x_2} & = -x_1-x_2(x_1^2+x_2^2) \\ \end{aligned} \right. {x1˙x2˙=x2−x1(x12+x22)=−x1−x2(x12+x22)
寻找平衡点:
{ x 2 − x 1 ( x 1 2 + x 2 2 ) = 0 − x 1 − x 2 ( x 1 2 + x 2 2 ) = 0 ⇒ x 1 = x 2 = 0 \left\{ \begin{aligned} x_2-x_1(x_1^2+x_2^2)& =0\\ -x_1-x_2(x_1^2+x_2^2) & =0 \\ \end{aligned} \right. \Rightarrow x_1=x_2=0 {x2−x1(x12+x22)−x1−x2(x12+x22)=0=0⇒x1=x2=0
选择V函数:
V ( x ) = x 1 2 + x 2 2 V(x)=x_1^2+x_2^2 V(x)=x12+x22
其中,
V ( x ) 正 定 V(x)正定 V(x)正定
V ˙ ( x ) = 2 x 1 x 1 ˙ + 2 x 2 x 2 ˙ = − 2 ( x 1 2 + x 2 2 ) 2 负 定 \dot{V}(x)=2x_1\dot{x_1}+2x_2\dot{x_2}=-2(x_1^2+x_2^2)^2负定 V˙(x)=2x1x1˙+2x2x2˙=−2(x12+x22)2负定
∴ 系 统 在 ( 0 , 0 ) 渐 进 稳 定 , 又 由 于 V ( x ) 半 径 无 穷 大 , 故 该 点 全 局 渐 进 稳 定 \therefore 系统在(0,0)渐进稳定,又由于V(x)半径无穷大,故该点全局渐进稳定 ∴系统在(0,0)渐进稳定,又由于V(x)半径无穷大,故该点全局渐进稳定
连续时间线性系统稳定性判别
线性时不变系统稳定判据的间接法
1
{ x 1 ˙ = x 2 x 2 ˙ = − x 1 \left\{ \begin{aligned} \dot{x_1} & = x_2\\ \dot{x_2} & = -x_1 \\ \end{aligned} \right. {x1˙x2˙=x2=−x1
A = [ 0 1 − 1 0 ] ⇒ d e t ( λ I − A ) = λ 2 + 1 ⇒ λ 1 , 2 = ± i A= \left[ \begin{matrix} 0 & 1 \\ -1 & 0 \end{matrix} \right]\Rightarrow det(\lambda I-A)=\lambda ^2+1\Rightarrow \lambda _{1,2}=\pm i A=[0−110]⇒det(λI−A)=λ2+1⇒λ1,2=±i
⇒ 系 统 所 有 平 衡 点 稳 定 \Rightarrow 系统所有平衡点稳定 ⇒系统所有平衡点稳定
2
{ x 1 ˙ = − x 1 + x 2 x 2 ˙ = − x 1 − x 2 \left\{ \begin{aligned} \dot{x_1} & = -x_1+x_2\\ \dot{x_2} & = -x_1-x_2 \\ \end{aligned} \right. {x1˙x2˙=−x1+x2=−x1−x2
A = [ − 1 1 − 1 − 1 ] ⇒ d e t ( λ I − A ) = ( λ + 1 ) 2 + 1 ⇒ λ 1 , 2 = − 1 ± i A= \left[ \begin{matrix} -1 & 1 \\ -1 & -1 \end{matrix} \right]\Rightarrow det(\lambda I-A)=(\lambda+1) ^2+1\Rightarrow \lambda _{1,2}=-1\pm i A=[−1−11−1]⇒det(λI−A)=(λ+1)2+1⇒λ1,2=−1±i
⇒ 系 统 所 有 平 衡 点 渐 进 稳 定 \Rightarrow 系统所有平衡点渐进稳定 ⇒系统所有平衡点渐进稳定
3
{ x 1 ˙ = x 1 + x 2 x 2 ˙ = − x 1 + x 2 \left\{ \begin{aligned} \dot{x_1} & = x_1+x_2\\ \dot{x_2} & = -x_1+x_2 \\ \end{aligned} \right. {x1˙x2˙=x1+x2=−x1+x2
A = [ 1 1 − 1 1 ] ⇒ d e t ( λ I − A ) = ( λ − 1 ) 2 + 1 ⇒ λ 1 , 2 = 1 ± i A= \left[ \begin{matrix} 1 & 1 \\ -1 & 1 \end{matrix} \right]\Rightarrow det(\lambda I-A)=(\lambda-1) ^2+1\Rightarrow \lambda _{1,2}=1\pm i A=[1−111]⇒det(λI−A)=(λ−1)2+1⇒λ1,2=1±i
⇒ 系 统 所 有 平 衡 点 不 稳 定 \Rightarrow 系统所有平衡点不稳定 ⇒系统所有平衡点不稳定
线性时不变系统稳定性判据的直接法
考虑 x ˙ = A x \dot{x}=Ax x˙=Ax的平衡点 x e = 0 x_e=0 xe=0稳定性,选择Lyapunov函数: V ( x ) = x T P x V(x)=x^TPx V(x)=xTPx
其中,P是正定矩阵, A T P + P A A^TP+PA ATP+PA是负定矩阵
V ˙ ( x ) = x ˙ T P x + x T P x ˙ = x T A T P x + x T P A x = x T ( A T P + P A ) x < 0 ( x ≠ 0 ) \dot{V}(x)=\dot{x}^TPx+x^TP\dot{x}=x^TA^TPx+x^TPAx=x^T(A^TP+PA)x<0(x\ne0) V˙(x)=x˙TPx+xTPx˙=xTATPx+xTPAx=xT(ATP+PA)x<0(x=0)