pytorch学习笔记（3）：常用网络层介绍

参考文档：https://mp.weixin.qq.com/s/Wxx-8b_36unlimLKBUl8zA

前两篇文章了解了如何用 pytorch 创建一个 CNN 网络，实现对 MNIST 数据集的图片分类。其中用到了一些函数，我们从字面意思也可以理解其功能。但是如何灵活自由的构建自己想要的网络结构呢？今天我们介绍一些在 Deep Learning 中经常听到的一些网络层，以及在 pytorch 中它们的使用方法。

1、常用的神经网络层

这里我们介绍一下在构建网络时常见的一些神经网络层，分别从卷积层，池化层，dropout，BN 层展开介绍。

卷积层

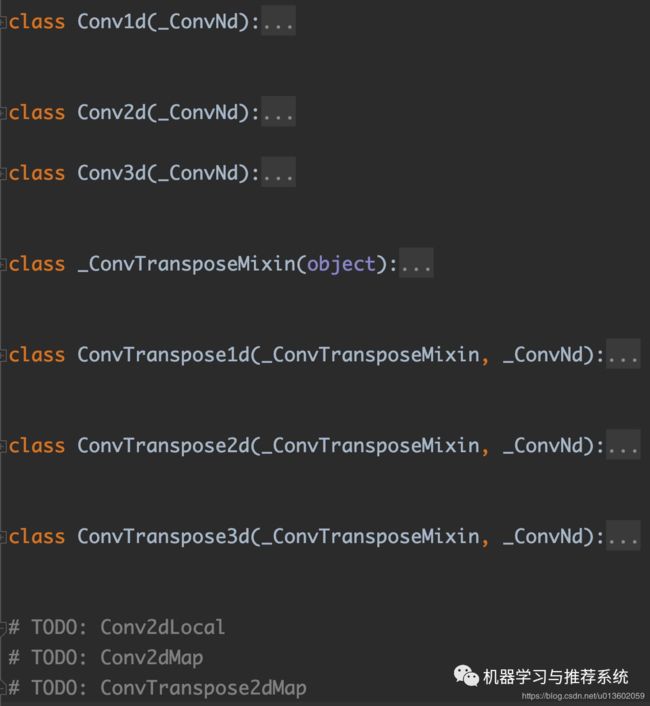
从上图的源码中我们可以看到，pytorch 提供了多种类型的卷积函数，后面的 TODO 也展示了 pytorch 开发团队在后面计划加入的一些层。

在我们平常的使用中，可能以二维卷积最常用，所以这里以它为例来进行介绍。

CLASS torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)

值得注意的几个点在于：
1.这是一个类，需要进行实例化后才能使用，我们使用的一般都是由这个类实例化出来的对象；
2.参数可以为 int 类型，也可以为 tuple，int 类型表示长宽都为同一个值；

接下来我们给一个例子看看：

>>> input = torch.randn(20, 16, 50, 100)

>>> # With square kernels and equal stride
>>> m = nn.Conv2d(16, 33, 3, stride=2)
>>> output = m(input)
>>> output.shape
torch.Size([20, 33, 24, 49])

>>> # non-square kernels and unequal stride and with padding
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
>>> output = m(input)
>>> output.shape
torch.Size([20, 33, 28, 100])

上面两个例子分别展示了参数为 int 和 tuple 的区别。大家也可以手推一下对输出的形状进行验证。

池化层

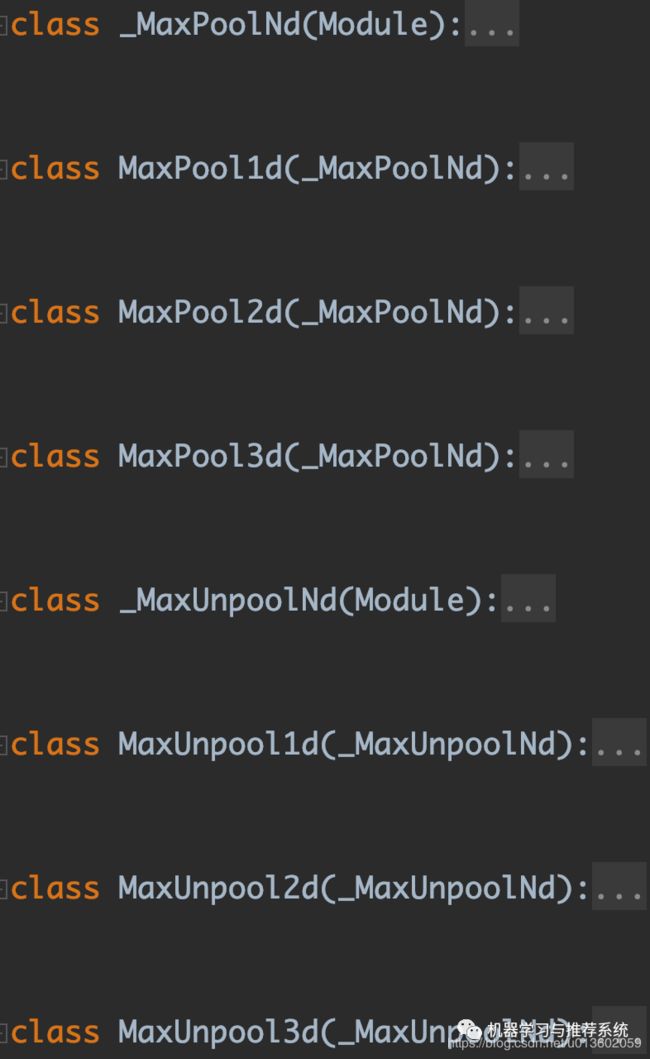
同样，这个图片截取了一部分源码中的示例，可以看到 pytorch 提供了很多类型的池化操作，我们以我们最常见的 max pooling 和 average pooling 为例进行介绍。

CLASS
torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True)

同样也是一个 class，我们也是使用实例化出来的对象进行网络操作。而且参数也可以选择 int 和 tuple 两种类型。

这里给出一个源码 doc 中的例子：

>>> input = torch.randn(20, 16, 50, 32)

>>> # pool of square window of size=3, stride=2
>>> m = nn.MaxPool2d(3, stride=2)
>>> output = m(input)
>>> output.shape
torch.Size([20, 16, 24, 15])

>>> # pool of non-square window
>>> m = nn.MaxPool2d((3, 2), stride=(2, 1))
>>> output = m(input)
>>> output.shape
torch.Size([20, 16, 24, 31])

dropout层

CLASS
torch.nn.Dropout(p=0.5, inplace=False)
torch.nn.Dropout2d(p=0.5, inplace=False)

Dropout 我们最常用的就是这两个，前者主要用于一维数据，比如 linear 的输出结果；后者主要用于二维数据，一般在卷积层后。其中的两个参数，p 表示一个将多少数据置为 0 的概率，inplace 为 true 则表示进行原地操作，对输入的数据本身内存进行操作。

下面给出一个源码 doc 中的例子：

>>> m = nn.Dropout2d(p=0.2)
>>> input = torch.randn(10, 3)
>>> output = m(input)
>>> input
tensor([[ 0.4453, -0.4929, -1.7591],
        [-0.1311, -1.0024, -0.5321],
        [-0.2614, -0.1416, -0.1580],
        [-0.1359,  0.0896, -0.3028],
        [-2.1673,  0.3533,  0.1597],
        [ 0.7464,  0.7417, -1.0306],
        [-0.1092, -1.0970,  1.1896],
        [ 0.7247, -0.8907,  0.6412],
        [ 1.9104, -0.1965,  1.6161],
        [ 0.0396,  0.4683, -0.4315]])
>>> output
tensor([[ 0.0000, -0.6161, -2.1988],
        [-0.1638, -1.2529, -0.6651],
        [-0.3268, -0.1770, -0.0000],
        [-0.1698,  0.0000, -0.3785],
        [-2.7091,  0.0000,  0.1996],
        [ 0.9330,  0.9271, -1.2882],
        [-0.0000, -1.3713,  1.4870],
        [ 0.0000, -1.1134,  0.8015],
        [ 2.3880, -0.2457,  0.0000],
        [ 0.0494,  0.5854, -0.0000]])

我们可以看到有一些数据被置为 0 了。

BN层

CLASS
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

这里的输入主要是需要注意一下 num_features，也就是输入数据的通道数。以二维的 BN 层为例，输入需要是一个 4 维的数据，分别是（batch_size，input_channel，H，W）。输出是一个同样维度的数据。

这里展示一下源码 doc 中的示例：

>>> # With Learnable Parameters
>>> m = nn.BatchNorm2d(100)

>>> # Without Learnable Parameters
>>> m = nn.BatchNorm2d(100, affine=False)

>>> input = torch.randn(20, 100, 35, 45)
>>> output = m(input)
>>> output.shape
torch.Size([20, 100, 35, 45])

可以看到输出数据的维度并没有变化，BN 层的输入需要和输入数据 input 的第二个维度保持一致（这里都是 100）。

2、常用的激活函数

在构建神经网络的过程中，激活函数也是非常重要的一个过程，对数据进行非线性激励，才是深度学习可以有如此优秀的拟合能力的核心。我们介绍几个比较典型的激活函数在 pytorch 中的应用。

这里的非线性激活函数，同样都是一个类，要使用需要进行实例化。具体的数学理论大家只要对 deep learning 的理论有些了解，对这些常见的激活函数肯定有所了解。

因为激活层一般输入和输出的格式是相同的，所以我们主要对这些激活函数的输入参数进行介绍，方便大家对这些激活层的应用。

elu

torch.nn.ELU(alpha=1.0, inplace=False)

$$ELU(x)=max(0,x)+min(0,\alpha \ast (exp(x)-1))$$输入的 alpha 就是上面函数中的 alpha。

relu

CLASS
torch.nn.ReLU(inplace=False)

relu 没有额外的参数要求，只是对数据直接进行操作。

sigmoid

CLASS
torch.nn.Sigmoid()

sigmoid 也没有额外的参数要求。

tanh

CLASS
torch.nn.Tanh()

同样没有额外的参数要求，输出与输入同格式。

softmax

CLASS
torch.nn.Softmax(dim=None)

同样没有额外的参数要求，输出与输入同格式。

最后我们给一个例子，大家可以参考一下代码应用形式：

>>> m = nn.ReLU()
>>> input = torch.randn(5)
>>> output = m(input)

>>> input
tensor([ 0.9920, -0.2270,  0.6381, -0.4804, -0.8548])
>>> output
tensor([0.9920, 0.0000, 0.6381, 0.0000, 0.0000])

3、损失函数

在网络训练的过程中，损失函数衡量了网络对数据的拟合能力。我们在这里简单介绍两类最常见的损失函数，这两个损失函数我们也在前面的两篇文章中分别用到了：MSE 和 CrossEntropy。

MSE

CLASS
torch.nn.MSELoss(size_average=None, reduce=None, reduction=’mean’)

同样是一个类，使用时需要进行实例化。MSE（均方误差） 一般用于回归任务中，衡量了输入 x 和 label 之间的误差程度。

得到的误差结合 backward() 可以自动求梯度。

CrossEntropy

CLASS
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction=’mean’)

这里一个需要注意的点是，CrossEntropyLoss 的输入是预测值和标签值，但是预测值是一个维度与类别数相等的张量，CrossEntropyLoss 会自动对输入进行一个 softmax() 操作，而标签值是对应的类别值。

下面我们给出一个例子，可以帮助我们进行理解。

>>> loss = nn.CrossEntropyLoss()
>>> input = torch.randn(3, 5, requires_grad=True)
>>> target = torch.empty(3, dtype=torch.long).random_(5)
>>> output = loss(input, target)

>>> input.shape
torch.Size([3, 5])
>>> target.shape
torch.Size([3])

4、总结

本篇文章我们介绍了一些常用的神经网络层，有了这些储备，我们基本上可以参考前面的两篇文章，来构建自己想要的神经网络结构。

更多的网络层的内容可以看 pytorch 官方文档的总结，都非常清晰：https://pytorch.org/docs/stable/nn.html#