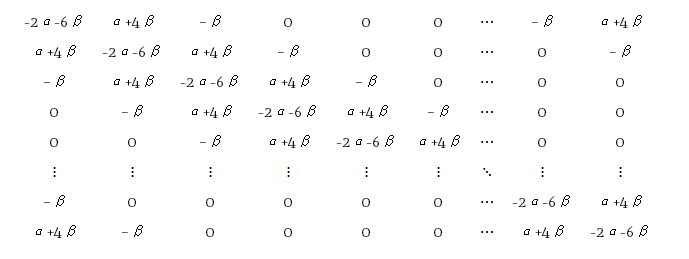itk中的图像分割算法(一)
Snake简介:
Snake的思路就是将目标图像的边缘检测转变为求解能量泛函最小值的过程。这类算法需要给出初始的轮廓,然后进行迭代,使轮廓沿能量降低的方向靠近,最后得到一个优化的边界。能量函数包括内外力两方面,如边界曲率和梯度。
优点:1.Snake模型基于Marr的计算机视觉理论,将高层信息和底层任务相结合,即把图像数据、目标边缘、初始估计和知识约束统一到一个过程中;
2.Snake模型的轮廓线在形变过程中自始自终都是连续光滑的,使得当我们提取局部间断或是不连续的边缘时,也会得到比较好的整体分割效果;
3.经过适当的初始化后,Snake模型会自动并自适应地收敛于目标边界处,不需要消耗太多人力;
4.Snake模型不会收到目标形状的约束,它可以检测出任意形状的边界,而且它是线性模型,可以快速执行自身形变,例如目标跟踪;
5.利用样条的平滑性约束作用,具有很强的鲁棒性。
缺点:
1.对初始轮廓位置比较敏感,初始轮廓必须设置在目标边缘附近,否则就会产生错误分割结果或是陷入局部最优;
2.比较依赖于参数,如何选取最有参数没有确定的准则;
3.不能自适应地改变自身的拓扑结构,因此很难同时分割多个目标;
4.传统Snack模型对于凹陷目标边缘的提取效果不好。
经典Snake模型:
0.Snake模型:1988年,Kass、Witkin和 Terzopoulos等人提出Active Contour Models,又叫Snake模型。这个轮廓同时收到三个能量驱使(内部的轮廓能量,用于保持snake在各阶导数上的连续性;图像能量,使得轮廓依附到所需要的特征上;外部约束能量),
1.Balloon-Snake模型:1991年,Cohen等人提出,将传统Snake模型里的高斯外力与新增加的膨胀力相结合,增大了外力捕获范围。
2.Distance-Snake模型:L.D.Cohen 和 I.Cohen 提出了基于距离势能的算法模型。
3.GVF-Snake模型:Xu Chenyang 等人在1998年提出。
接下来看代码:
1.创建初始图像数据
void createImage(ImageType::Pointer image,
int w, int h, double cx, double cy, double rx, double ry)
{
itk::Size<2> size;
size[0] = w;
size[1] = h;
//生成一个随机图像
itk::RandomImageSource::Pointer randomImageSource = itk::RandomImageSource::New();
randomImageSource->SetNumberOfThreads(1); // to produce non-random results
randomImageSource->SetSize(size);//大小
randomImageSource->SetMin(200);//最小灰度
randomImageSource->SetMax(255);//最大灰度
randomImageSource->Update();
image->SetRegions(randomImageSource->GetOutput()->GetLargestPossibleRegion());
image->Allocate();
IndexType index;
//Draw oval.
for (int i=0; iSetPixel(index, randomImageSource->GetOutput()->GetPixel(index)-100);
}
else
{
image->SetPixel(index, randomImageSource->GetOutput()->GetPixel(index));
}
}
}
} vnl_vector generateCircle(double cx, double cy, double rx, double ry, int n)
{
vnl_vector v(2*(n+1));
for (int i=0; i vnl_matrix computeP(double alpha, double beta, double gamma, double N) throw (int)
{
double a = gamma*(2*alpha+6*beta)+1;
double b = gamma*(-alpha-4*beta);
double c = gamma*beta;
vnl_matrix P(N,N);
P.fill(0);
//fill diagonal 填充对角线
P.fill_diagonal(a);
//fill next two diagonals 填充接下来的两条对角线
for (int i=0; i<(N-1); i++)
{
P(i+1,i) = b;
P(i,i+1) = b;
}
//Moreover 另外
P(0, N-1)=b;
P(N-1, 0)=b;
//fill next two diagonals
for (int i=0; i<(N-2); i++)
{
P(i+2,i) = c;
P(i,i+2) = c;
}
//Moreover
P(0, N-2)=c;
P(1, N-1)=c;
P(N-2, 0)=c;
P(N-1, 1)=c;
if ( vnl_determinant(P) == 0.0 )
{
std::cerr << "Singular matrix. Determinant is 0." << std::endl;
throw 2;
}
//Compute the inverse of the matrix P 计算矩阵p的逆矩阵
vnl_matrix< double > Pinv;
Pinv = vnl_matrix_inverse< double >(P);
return Pinv.transpose();
} vnl_vector sampleImage(vnl_vector x, vnl_vector y, OutputImageType::Pointer gradient, int position)
{
int size;
size = x.size();
vnl_vector ans(size);
IndexType index;
for (int i=0; iGetPixel(index)[position];
}
return ans;
} #include "vnl/vnl_math.h"
#include
#include "vnl/algo/vnl_determinant.h"
#include "vnl/algo/vnl_matrix_inverse.h"
#include
int main( int argc, char* argv[] )
{
//Image dimensions
int w = 300;
int h = 300;
ImageType::Pointer image = ImageType::New();
createImage(image, w, h, 150, 150, 50, 50); //创建图像
//Snake parameters
double alpha = 0.001;//0.01
double beta = 0.4;//0.4
double gamma = 100;//0.07
double iterations = 1;//6000
int nPoints = 20;//100
double sigma;//4
//Temporal variables 时间变量?
vnl_vector v = generateCircle(130, 130, 50, 50, nPoints); //创建一个圆
double N = v.size()/2;
vnl_matrix P = computeP(alpha, beta, gamma, N);//获得一个初始化的矩阵(整个算法核心内容就是这个矩阵)
//Computes the magnitude gradient
//计算图像的幅度梯度图
//itkGradientMagnitudeImageFilter
GradMagfilterType::Pointer gradientMagnitudeFilter = GradMagfilterType::New();
gradientMagnitudeFilter->SetInput( image );
gradientMagnitudeFilter->Update();
//Computes the gradient of the gradient magnitude
//计算图像幅度梯度图的梯度图(哈哈,不敢相信了,二阶导数)
//itkGradientRecursiveGaussianImageFilter
FilterType::Pointer gradientFilter = FilterType::New();
gradientFilter->SetInput( gradientMagnitudeFilter->GetOutput() );
gradientFilter->SetSigma( sigma );
gradientFilter->Update();
//Loop
vnl_vector x(N);
vnl_vector y(N);
std::cout << "Initial snake" << std::endl;//开始snake计算
for (int i = 0; i < N; i++)//将二维圆降维成一维数组
{
x[i] = v[2*i];
y[i] = v[2*i+1];
std::cout << "(" << x[i] << ", " << y[i] << ")" << std::endl;
}
for (int i = 0; i < iterations; i++)//iterations 迭代次数,看预设参数需要6000?有点多吧?
{
vnl_vector fex;
vnl_vector fey;
//该点在图像幅度梯度图的梯度值
fex = sampleImage(x, y, gradientFilter->GetOutput(), 0);
fey = sampleImage(x, y, gradientFilter->GetOutput(), 1);
//计算后刷新xy (原来的点+该点在灰度图的邻域梯度值)*矩阵
//为了离散化的时间参数,增加一个步长gamma
// ∂Xt / ∂t = (Xt–Xt-1) / γ
// Xt = (I – γA)-1{Xt-1 + γ fx(Xt-1,Yt-1)}
// Yt = (I – γA)-1{Yt-1 + γ fy(Xt-1,Yt-1)}
x = (x+gamma*fex).post_multiply(P);//post_multiply 矩阵左乘
y = (y+gamma*fey).post_multiply(P);
}
//Display the answer
std::cout << "Final snake after " << iterations << " iterations" << std::endl;
vnl_vector v2(2*N);//将结果存在这里,将一维结果升维
for (int i=0; i 思路详解(原文在参考文献7,感谢原作者):
Snake(主动轮廓模型),就是通过一条可变的离散化二维曲线来描述目标图像的边缘轮廓,当该曲线能量最小化时就是目标图像的边缘轮廓的最优解。
这条曲线通过一个变量p(0,1)参数化,这样就可以将曲线从二维降到一维:x(p) 和 y(p)。为了简单期间,再转换到向量空间: s(p) = (x(p),y(p))T。
snake二维曲线通常是封闭曲线,所以 s(0) = s(1)。
这样,最小化能力函数就可以定义为:
E = ∫ Eint(s(p)) + Eext dp(s(p))
Eint 代表内部能量,负责约束曲线形状,
Eext 代表外部能量,负责开拓曲线边缘,外部能量通常是数字图像中梯度幅值的逆矩阵:越靠近边缘能量越低,越远离边缘能量越高(Kass, Witkin and Terzopoulos (1988) 在论文中做出了定义)。
先来讨论内部能量Eint ,
Eint(s(p)) = ½ { α(p)|s′(p)|2 + β(p)|s″(p)|2 }
α 和 β 是两个预设参数,曲线上每点的α 和 β 都是相同的。
一阶导数越大,曲线的长度越长,目的是约束曲线的长度;
二阶导数越大,曲线的曲率越大,目的是约束曲线的曲率;
接下来讨论外部能量Eext ,
通过Euler–Lagrange equation(欧拉-拉格朗日方程),最终得出:
αs″(p) – βs″″(p) – ∇Eext(s(p)) = O
∇Eext :外部能量的梯度;(算法的重点就在这里)
将上面的s(p)函数转换成时间函数s(p,t),O转换为s(p,t)在t的偏导数,于是有:
∂s(p)/∂t =αs′(p, t)-βs′′(p, t)+ Fext(s(p, t))
接下来要做的是i,将曲线方程离散化,
p = i/N ,(i 区间为(0,N-1))
而snake曲线是封闭的,所以有s[N] = s[0], s[N+1] = s[1], ,,,
然后将二维曲线降维,Fext 用 fx 和 fy 来表示。我们使用有限差分法来逼近空间导数:
x″[i] = x[i-1]-2x[i]+x[i+1]
x″″[i] = x[i-2]-4x[i-1]+6x[i]-4x[i+1]+x[i+2]
于是有:
∂xt[i] / ∂t = α(xt[i-1]-2xt[i]+xt[i+1]) + β(-xt[i-2]+4xt[i-1]-6xt[i]+4xt[i+1]-xt[i+2]) + fx(xt[i],yt[i])
∂yt[i] / ∂t = α(yt[i-1]-2yt[i]+yt[i+1]) + β(-yt[i-2]+4yt[i-1]-6yt[i]+4yt[i+1]-yt[i+2]) + fy(xt[i],yt[i])
接下来是神来之笔:
构建一个五循环对角带状矩阵!如下:
∂Xt / ∂t = AXt + fx(Xt,Yt)
∂Yt / ∂t = AYt + fy(Xt,Yt)
最后一步,要在离散化的时间参数上增加一个步长 γ: ∂Xt / ∂t = (Xt–Xt-1) / γ.
假设snake运动范围足够小,步伐足够慢,那么就可以将t-1带入上面的方程:
Xt = (I – γA)-1{Xt-1 + γ fx(Xt-1,Yt-1)}
Yt = (I – γA)-1{Yt-1 + γ fy(Xt-1,Yt-1)}
这就是简化后的snake了。
思路的转换往往能带来持久的惊喜,Snake方法就是在图像分割领域的惊喜之一。
抱歉在介绍分割算法的第一篇就放大招,基础的分割算法之后会陆续补齐的,并且深入分析源代码,争取揭掉图像处理算法面纱,看到数学矩阵变换真相。
1.https://itk.org/Wiki/ITK/Examples/ImageSegmentation/ExtractContourWithSnakes
2.http://www.cnblogs.com/lcchuguo/p/4046372.html
3.http://blog.csdn.net/byxdaz/article/details/667432?locationNum=12
4.《Snake模型图像分割算法研究》
5.https://zhidao.baidu.com/question/743867243241521212.html
6.《对snake模型的研究》
7.http://www.crisluengo.net/index.php/archives/217