初赛问题求解选集
zhowie大佬传送门
YZK大佬传送门
社会瑞姐传送门
NOIP2005
第一题
答案:5。
解析:选择排序的原理。对于按顺序扫描的i,每次在i的后面选择一个最小的和i交换。
这5次分别交换( 32,25 ),( 74,28 ),( 43,53 ),( 58,47 ),( 47,86 )
第二题
答案:11011.
解析:当此时有x根火柴,当且仅当x%3==0时,x是必败的。
反之,如果x%3=a( a!=0 )那么先手先取a,剩下的数是3的倍数。每一轮无论后手怎么取(假设取b),先手都取( 3-b )让每一轮都恰好取走3个,可以保证让先手取走最后一批。
NOIP2012
第一题
本题中,我们约定布尔表达式只能包含p,q,r三个布尔变量,以及“与”(∧)、“或”(∨)、“非”(¬)三种布尔运算。如果无论p,q,r如何取值,两个布尔表达式的值总是相同,则称它们等价。例如(p∨q)∨r和p∨(q∨r)等价,p∨¬p和q∨¬q也等价;而p∨q和p∧q不等价。那么两两不等价的布尔表达式最多有_个。
答案:256。
题解
这道题该怎么去思考?
由于无论怎么取,两个式子的值恒等。p,q,r可以取0,1中的任意一个数,总共有2³=8种情况,每种情况对应一个不同的值,0或1。
因此每种情况都对应一个字符串,保证字符串的值不等,两两都不等价,至少有2^8种取法,因此答案就是256
第二题
2. 对于一棵二叉树,独立集是指两两互不相邻的节点构成的集合。例如,图1有5个不同的独立集(1个双点集合,3个单点集合、1个空集),图2有14个不同的独立集。那么图3有 ___个不同的独立集。
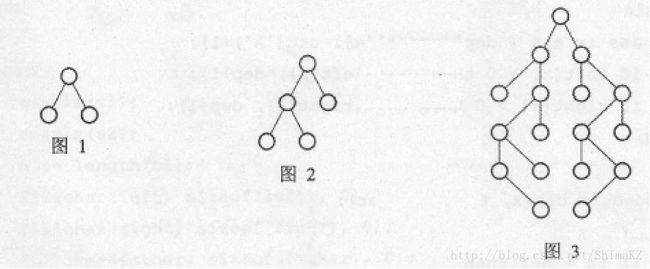
这道题考虑的是树形DP,对于每一个节点,可以得到如下递推式:
(a[i]表示的是第选的方案,b[i]表示的是不选的方案)
a[i]=(a[left]+b[left])*(a[right]+b[right]);//左右节点选或不选的方案数的总和。
b[i]=a[left]*a[right];//不选左右节点的方案数的总和。
最后只要求出a[1]+b[1]即可
NOIP2014
第一题
直接枚举都可以写出来,但可以分类讨论去写。
I.组成的四位数中有4种不同的数,取法只有一种,1,2,4,8,总共1×A(4,4)=24个。
II.组成的四位数有3种不同的数,两个1的取法有3种,两个8的取法也有3种,总共6×A(4,4)/A(2,2)=72个。
III.组成的四位数有2种不同的数,取法只有一种,1,1,8,8,总共A(4,4)/(A(2,2)×A(2,2))=6个。
总共24+72+6=102个。
第二题
想用什么算法就用什么算法,反正能过就行
NOIP2013
第一题
水题,模拟
第二题
这道题我其实已经算出来了,只不过最后大意了,忘了除以4,导致了错误。这也是一个递推的问题,因此可以算过去。
设从2跳到1的期望是f2,那么有1/2的概率是一次跳到1,还有1/2的概率是(1+f2)次跳到1,
即第一次没有跳到1,跳到2的情况,
于是可以列出等式:f2=1*1/2+(1+f2)*1/2,得f2=2;对于n=3,则有1/3的概率一次跳到1,有1/3的概率(1+f2)次跳到1,即第一次跳到2,再从2跳到1的过程,
最后还有1/3的概率(1+f3)次跳到1,于是f3=1/3+(1+f2)*1/3+(1+f3)*1/3,
得f3=2.5;
同理f4=1/4+(1+f2)*1/4+(1+f3)*1/4+(1+f4)*1/4,
得f4=17/6;
f5=1/5+(1+f2)*1/5+(1+f3)*1/5+(1+f4)*1/5+(1+f5)*1/5,
得f5=37/12. NOIP2011
第一题
画一下就出来了.
第二题
这道题我是直接意识流玄学过的,但真正的方法是LIS的做法
这个不是交换位置喔,是取出再插入。
先在原序列中找个最长上升子序列(除去某些元素,但不影响相对位置的序列称为子序列),发现是ACEGI,长度为5,最长了,
剩下4个移动一下就能成有序的ABCDEFGHI了NOIP2010
第一题
这个跟送的一样,然而我多抄了一个空格,5分没了。以后一定要注意在记录答案的时候也要认真一些,不要随便搞搞就过去了。
第二题
这个条件我没看懂,其实分析一下就是个二分图。补充一个定理:
定理:无向图G为二分图的充分必要条件是:G至少有两个顶点,且其所有回路的长度均为偶数。第三题
这道题挺难的,用前缀和以及构造图来写,具体实现,商业机密
NOIP2009
第一题
先确定12346的位置,然后将7插入内部有两个位置可选,然后将5插入时候,有6个位置选择。最后,放89的时候,考虑两种情况,89在一起,有8个位置选;89不在一起,8个位置选2个。
第二题
先化成七进制数,因为可以无限找零,所以把大于4的位数用7-a代替,即可得解。
NOIP2006&NOIP2007
见考后总结NOIP2006,NOIP2007。
未完待续。。。