工厂最大效益--单纯性算法

运气好不好，我学了运筹学，没选到数学建模，但是我觉得运筹学作为一门比较接近优化各种算法的学科，我还是比较喜欢的，下面记录的是我在运筹学第一章中学习的单纯性算法的运用。此处不详细讲解单纯性算法原理了，附上链接（百度百科-单纯性算法）

---

本博文参考《趣学算法》实现，仅学习使用，侵删。

---

单纯性算法

概念：
单纯形法是一种迭代算法，其基本原理及主要步骤是：首先设法找到一个（初始）基可行解，然后再根据最优性理论判断这个基可行解是否最优解。若是最优解，则输出结果，计算停止；若不是最优解，则设法由当前的基可行解产生一个目标值更优的新的基可行解，再利用最优性理论对所得的新基可行解进行判断，看其是否最优解，这样就构成一个迭代算法。由于基可行解只有有限个，而每次目标值都有所改进，因而必可在有限步内终止。如果原问题确有最优解，必可在有限步内达到，且计算量大大少于穷举法；若原问题无最优解，也可根据最优性理论及时发现，停止计算，避免错误及无效运算。

标准数学表达式如下：（图片来源于百度百科）

---

题目：（来源于《趣学算法》）
某食品加工厂一共有三个车间，第一车间用1个单位的原料N可以加工5个单位的产品A或2个单位的产品B。产品A如果直接售出，售价为10元，如果在第二车间继续加工，则需要额外加工费5元，加工后售价为19元。产品B如果直接售出，售价16元，如果在第三车间继续加工，则需要额外加工费4元，加工后售价为24元。原材料N的单位购入价为5元，每工时的工资是15元，第一车间加工一个单位的N,需要0.05个工时，第二车间加工一个单位需要0.1工时，第三车间加工一个单位需要0.08工时。每个月最多能得到12000单位的原材料N,工时最多为1000 工时。如何安排生产，才能使工厂的效益最大呢?

---

1.目标函数和约束条件如下:
max z = 10x1 +12.5x2 + 16x3 +18.8x4 - 5.75x5;
x3+4-2x5 = 0;
x5 ≤ 12000;
0.1x2 + 0.08x4 +0.05x5 ≤ 1000;
xi ≥ 0(i=1,2,3, 4,5);
其中
x1表示产品A的售出量
x2表示产品A在第二车间加工后的售出量
x3表示产品B的售出量
x4表示产品B在第三车间加工后的售出量
x5表示第一车间所用的原材料数量

max z = 10x1 +12.5x2 + 16x3 +18.8x4 - 5.75x5;
表示A直接售出的价钱+

x1 +x2-5x5 = 0;
表示产品A在第一车间使用原料一共可以生产的数量

x3+x4-2x5 = 0;
表示产品B在第一车间使用原料一共可以生产的数量

x5 ≤ 12000
表示原料的最大值

0.1x2 + 0.08x4 +0.05x5 ≤ 1000;
表示在一二三车间使用的工时的满足式

2.转化为标准型
max z = 10x1 +12.5x2 + 16x3 +18.8x4 - 5.75x5;
x1 +x2-5x5 = 0;
x3+x4-2x5 = 0;
x5 + x6 = 12000;
0.1x2 + 0.08x4 +0.05x5 + x7 = 1000;
xi ≥ 0(i=1,2,3, 4,5,6,7)

3.建立单纯形表
四个表达式，需要四个基本变量，查看可知:x1,x3,x6,x7可作为基向量
（x1,x3,x6,x7);
将目标函数有非基变量表示可得：
z = 2.5x2+2.8x4,+76.25x5;
在单纯性表中，基变量做行，非基变量做列，检验数放第一行，非基变量的系数作为值，走早初始单纯形表；

4.判断是否得到最优解
1.若c所在行的检验数都小于等于零，那么就获得了最优解；
2.若存在某检验数有为正数，但是正数所在列向量存在各分量均小于等于零，那么该问题无有解界；
3.若检验数中存在为正数，并且所在列向量中有值为正数，那么继续计算即可；

5.选入基变量
正检验数中最大的一个数所对应的非基变量xn为入基变量，xn所对应的列为入基列；

6.选离基变量
选取“常数列元素/入基列元素”正比值的最小者，所对应的非基变量xm为离基变量，xm所对应的行为离基行；

7.换基变换
在单纯形表中将入基变量xn和离基变量xm变换位置

8.建立新的单纯形表
入基列 = -原值/交叉值（不包括交叉位）；
离基行 = 原值/交叉值（不包括交叉位）；
交叉位 = 原值取倒数；
c0位 = 原值 + 同行入基列元素 * 同列离基行元素/ 交叉位值：0 + 76.25 * 12000 / 1 = 915 000;

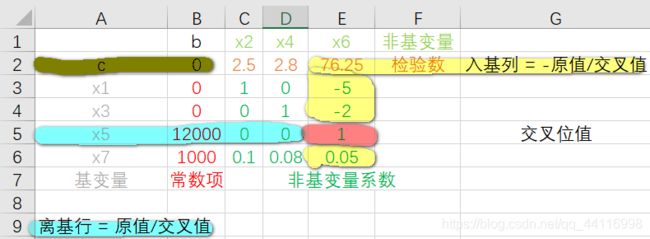
一般位置元素 = 原值 - 同行入基列元素 * 同列离基行元素/ 交叉位值；

9.判断是否得到最优解
若没有，继续执行5–8步骤；
判断有最优解，全部检验数均小于等于零，因此得到最优解，c0就是最优解，而最优解是由基变量对应的常数成的，即b所在的列，非基变量全部取零，得到唯一的最优解基向量：

---

代码实现

#include
#include
#include
using namespace std;
float kernel[100][100];//单纯形表
char FJL[100] = { };//非基变量
char JL[100] = { };//基变量
int n, m, i, j;
void Print()//输出单纯形表
{
	cout << "------------单纯形表如下------------" << endl;
	cout << "  ";
	cout << setw(7) << "b ";
	for (i = 1; i < n; i++)//非基变量输出
		cout << setw(7) << "x" << FJL[i];
	cout << endl;
	cout << "c ";
	for (i = 0; i <= n; i++)
	{
		if (i >= 1)
			cout << "x" << JL[i];
		for (j = 0; j <= m; j++)
			cout << setw(7) << kernel[i][j] << " ";
		cout << endl;
	}
	return;
}
void DCXA()
{
	float max1;//存放最大的检验数
	float max2;//存放最大正检验数对应的基变量的最大系数
	int e = -1;//记录入基列
	int k = -1;//记录离基行
	float min;
	while (true)//循环迭代，直到找到问题的解或者无解为止
	{
		max1 = 0;
		max2 = 0;
		min = 100000000;
		for (j = 1; j <= m; j++)//找入基列
		{
			if (max1 < kernel[0][j])
			{
				max1 = kernel[0][j];
				e = j;
			}
		}
		if (max1 <= 0)//最大值<=0
		{
			cout << endl;
			cout << "获得最优解： " << kernel[0][0] << endl;
			for(i = 1 ;i <= n;i++)
				cout<<"x"<<JL[i]<<"="<<kernel[i][0]<<"  "; 
			cout<<"其余变量为零"<<endl; 
			break;
			}
		for (j = 1; j <= m; j++)//判断检验数对应列的如果都小于等于零，则无解
		{
			max2 = 0;
			if (kernel[0][j] > 0)
			{
				for (i = 1; i <= n; i++)//正检验数所对应列
					if (max2 < kernel[i][j])
						max2 = kernel[i][j];
				if (max2 <= 0)
				{
					cout << "解无界" << endl;
					return;
				}
			}
		}
		for (i = 1; i <= n; i++)//找离基行
		{
			float temp = kernel[i][0] / kernel[i][e];
			if (temp > 0 && temp < min)
			{
				min = temp;
				k = i;
			}
		}
		cout << "入基变量 " << "x" << FJL[e] << " ";
		cout << "出基变量 " << "x" << JL[k] << " "<<endl<<endl;
		char temp = FJL[e];//变基变换
		FJL[e] = JL[k];
		JL[k] = temp;
		for (i = 0; i <= n; i++)//计算除入基列和出基行的所有位置的元素
		{
			if (i != k)
			{
				for (j = 0; j <= m; j++)
				{
					if (j != e)
					{
						if (i == 0 && j == 0)//特殊位置c0
							kernel[i][j] = kernel[i][j] + kernel[i][e] * kernel[k][j] / kernel[k][e];
						else//一般位置
							kernel[i][j] = kernel[i][j] - kernel[i][e] * kernel[k][j] / kernel[k][e];
					}
				}
			}
		}
		for (i = 0; i <= n; i++)//入基列元素
		{
			if (i != k)
				kernel[i][e] = -kernel[i][e] / kernel[k][e];
		}
		for (j = 0; j <= m; j++)//离基行元素
		{
			if (j != e)
				kernel[k][j] = kernel[k][j] / kernel[k][e];
		}
		kernel[k][e] = 1 / kernel[k][e];//交叉位置取倒数
		Print();
	}
	return;
}
int main()
{
	cout << "请输入非基变量个数和非基变量的下标:" << endl;
	cin >> m;
	for (i = 1; i <= m; i++)
		cin >> FJL[i];
	cout << "请输入基变量个数和基变量的下标:" << endl;
	cin >> n;
	for (i = 1; i <= n; i++)
		cin >> JL[i];
	cout << "输入约束标准型初始单纯形表的参数:" << endl;
	for (i = 0; i <= n; i++)
	{
		for (j = 0; j <= m; j++)
			cin >> kernel[i][j];
	}
	Print();
	DCXA();
	system("pause");
	return 0;
}

运行效果