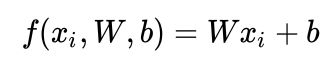以下内容参考CS231n。
上一篇关于分类器的文章，使用的是KNN分类器，KNN分类有两个主要的缺点：
- 空间上，需要存储所有的训练数据用于比较。
- 时间上，每次分类操作，需要和所有训练数据比较。
本文开始线性分类器的学习。
和KNN相比，线性分类器才算得上真正具有实用价值的分类器，也是后面神经网络和卷积神经网络的基础。
线性分类器中包括几个非常重要的部分：
- 权重矩阵W，偏差向量b
- 评分函数
- 损失函数
- 正则化
- 最优化
权重矩阵W （Weights）
- 可以理解为所有分类对应的模版向量w组成的矩阵，模版就是分类期望成为的样子。
- 训练数据可以理解为是N维空间中的一个向量v，v和W中每个模版做点积，点积越大，表示两个向量的夹角越小，也就越接近。
- 点积最大的模版w，就是v所对应的分类。
- W不是一直不变的。它会随着对损失函数最优化的过程，不断的调整。
偏差向量b （bias vector）
b是不是可以理解为，如果不设置b，那所有的分类线都要通过原点，那其实就起不到分类的作用了？
参考下图？三条线都通过原点，是无法对数据做分类的。
W和b分别对直线做旋转和平移。
评分函数（score function）
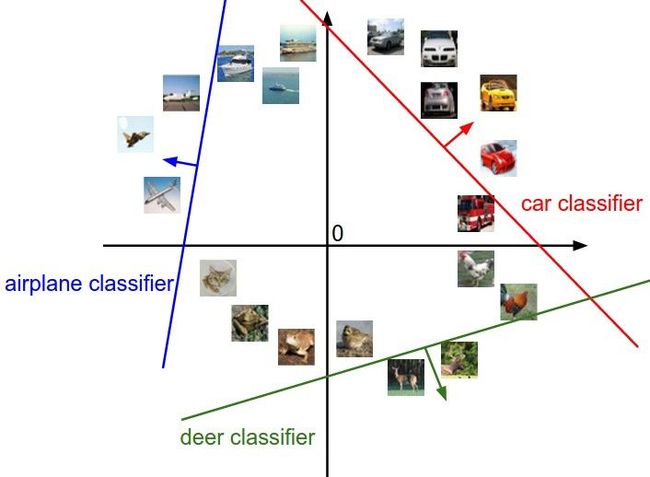
之所以是线性分类器，就是因为评分函数使用线性方程计算分数。后面的神经网络会对线性函数做非线性处理。
下图直观的展示了分类器的线性。
损失函数 （loss function）
如何判断当前的W和b是否合适，是否能够输出准确的分类？
通过损失函数，就可以计算预测的分类和实际分类之间的差异。通过不断减小损失函数的值，也就是减少差异，就可以得到对应的W和b。
Python实现
数据预处理
# 每行均值
mean_image = np.mean(X_train, axis=0) # second: subtract the mean image from train and test data # 零均值化，中心化，使数据分布在原点周围，可以加快训练的收敛速度 X_train -= mean_image X_val -= mean_image X_test -= mean_image X_dev -= mean_image
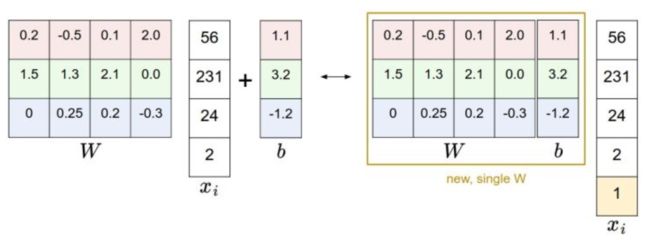
处理b的技巧
# third: append the bias dimension of ones (i.e. bias trick) so that our SVM # only has to worry about optimizing a single weight matrix W. # 技巧，将bias加到矩阵中，作为最后一列，直接参与矩阵运算。不用单独计算。 # hstack，水平地把数组的列组合起来 # 每行后面 加一个元素1 X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))]) X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))]) X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))]) X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])
计算损失函数
使用多类支持向量机作为损失函数。 SVM loss function,
, 
全体训练集上的平均损失值：
为了体现向量计算的高效，这里给出了非向量计算作为对比。
非向量版：
1 # 多类支持向量机损失函数 2 # SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值Delta 3 # max(0, s1 - s2 + delta) 4 # s1,错误分类， s2，正确分类 5 def svm_loss_naive(W, X, y, reg): 6 7 # N, 500 8 # D, 3073 9 # C, 10 10 # W (3073, 10), 用（1，3073）左乘W，得到（1， 10） 11 # X(500, 3073), y(500,) 12 13 # 对W求导。 后面求使损失函数L减小的最快的w，也就是梯度下降最快的方向。 14 dW = np.zeros(W.shape) # initialize the gradient as zero 15 16 # compute the loss and the gradient 17 num_classes = W.shape[1] # 10 18 num_train = X.shape[0] # 500 19 loss = 0.0 20 for i in range(num_train): 21 # 分数 = 点积 22 # 向量(1,D)和矩阵(D,C)的点积 = (1,C) (c,) 23 # scores中的一行，表示所有类的打分 24 scores = X[i].dot(W) 25 26 # y[i]，对的分类 27 correct_class_score = scores[y[i]] 28 for j in range(num_classes): 29 # 相等的分类不做处理 30 if j == y[i]: 31 continue 32 # 用其他分类的得分 - 最终分类的得分 + 1 33 margin = scores[j] - correct_class_score + 1 # note delta = 1 34 35 if margin > 0: 36 loss += margin 37 38 # （错的-对的），所以第一个是-X，第二个是X 39 # 500张图片的dW和，后面再除个500 40 dW[ :, y[i] ] += -X[ i, : ] 41 dW[ :, j ] += X[ i, : ] 42 43 loss /= num_train 44 dW /= num_train 45 46 # Add regularization to the loss. 47 # 正则化，https://blog.csdn.net/gsww404/article/details/80414675 48 # L2正则化 49 loss += reg * np.sum(W * W) 50 51 # 这里为什么不是2W 52 dW += reg * W 53 54 return loss, dW
向量版：
def svm_loss_vectorized(W, X, y, reg): loss = 0.0 dW = np.zeros(W.shape) # initialize the gradient as zero num_classes = W.shape[1] num_train = X.shape[0] scores = X.dot(W) # (500, 10) correct_scores = scores[ np.arange(num_train), y] #(500, ), 取( 0～500， y[0~500]) correct_scores = np.tile(correct_scores.reshape(num_train, 1) , (1, num_classes)) # (500, 10), 复制出10列，一行里的值是相同的 margin = scores - correct_scores + 1 margin[np.arange(num_train), y] = 0 # 正确的分类，不考虑 margin[margin < 0] = 0 # 小于0的置为0，不考虑 loss = np.sum(margin) / num_train loss += reg * np.sum(W * W) margin[ margin > 0 ] = 1 # 大于0的是造成损失的权重 row_sum = np.sum( margin, axis = 1 ) # 对每行取和， dW[ :, y[i] ] += -X[ i, : ]， 参考非向量的写法，每次遍历里，正确的分类都有被减一次 margin[np.arange( num_train ), y] = -row_sum # 正确分类是负的，-X # 点积 dW += np.dot(X.T, margin) / num_train + reg * W return loss, dW
随机初始化W，计算loss和gradient
# randn，高斯分布（正态分布）随机数 # 初始权重采用小一点的值 W = np.random.randn(3073, 10) * 0.0001
# grad，analytic gradient loss, grad = svm_loss_naive(W, X_dev, y_dev, 0.000005)
检查梯度值的正确性。用数值梯度值（numerical gradient）和分析梯度值（analytic gradient）比较。
检查梯度方法：
def grad_check_sparse(f, x, analytic_grad, num_checks=10, h=1e-5): for i in range(num_checks): # 随机取一个位置 ix = tuple([randrange(m) for m in x.shape]) oldval = x[ix] x[ix] = oldval + h # increment by h fxph = f(x) # evaluate f(x + h) x[ix] = oldval - h # increment by h # decrement ？ fxmh = f(x) # evaluate f(x - h) x[ix] = oldval # reset # 对称差分 grad_numerical = (fxph - fxmh) / (2 * h) grad_analytic = analytic_grad[ix] # 相对误差 ？？ rel_error = abs(grad_numerical - grad_analytic) / (abs(grad_numerical) + abs(grad_analytic))
比较分析梯度和数值梯度：
# 检查计算的梯度值是否正确 # Compute the loss and its gradient at W. loss, grad = svm_loss_naive(W, X_dev, y_dev, 0.0) # Numerically compute the gradient along several randomly chosen dimensions, and # compare them with your analytically computed gradient. The numbers should match # almost exactly along all dimensions. from cs231n.gradient_check import grad_check_sparse f = lambda w: svm_loss_naive(w, X_dev, y_dev, 0.0)[0] # 取loss grad_numerical = grad_check_sparse(f, W, grad) # do the gradient check once again with regularization turned on # you didn't forget the regularization gradient did you? loss, grad = svm_loss_naive(W, X_dev, y_dev, 5e1) f = lambda w: svm_loss_naive(w, X_dev, y_dev, 5e1)[0] grad_numerical = grad_check_sparse(f, W, grad)
创建一个线性分类器类
最优化方法使用 随机梯度下降法（SGD，Stochastic Gradient Descent）。
class LinearClassifier(object): def __init__(self): self.W = None # 训练，也是最优化，调参的过程。 def train(self, X, y, learning_rate=1e-3, reg=1e-5, num_iters=100, batch_size=200, verbose=False): """ Train this linear classifier using stochastic gradient descent. Inputs: - X: A numpy array of shape (N, D) containing training data; there are N training samples each of dimension D. - y: A numpy array of shape (N,) containing training labels; y[i] = c means that X[i] has label 0 <= c < C for C classes. C是所有类别吧？ - learning_rate: (float) learning rate for optimization. - reg: (float) regularization strength. - num_iters: (integer) number of steps to take when optimizing - batch_size: (integer) number of training examples to use at each step. - verbose: (boolean) If true, print progress during optimization. Outputs: A list containing the value of the loss function at each training iteration. """ num_train, dim = X.shape num_classes = np.max(y) + 1 # assume y takes values 0...K-1 where K is number of classes if self.W is None: self.W = 0.001 * np.random.randn(dim, num_classes) loss_history = [] for it in range(num_iters): X_batch = None y_batch = None # 默认是replacement = true， 随机出来的数，还要再放回到样本池中 randomRows = np.random.choice(num_train, batch_size) X_batch = X[randomRows] y_batch = y[randomRows] # evaluate loss and gradient loss, grad = self.loss(X_batch, y_batch, reg) loss_history.append(loss) # perform parameter update self.W += -learning_rate * grad if verbose and it % 100 == 0: print('iteration %d / %d: loss %f' % (it, num_iters, loss)) return loss_history # 预测 def predict(self, X): y_pred = np.zeros(X.shape[0]) y_pred = np.argmax( np.dot( X, self.W ), axis=1 ) return y_pred # 计算损失值 def loss(self, X_batch, y_batch, reg): pass
继承基类LinearClassifier，定义SVM分类器
class LinearSVM(LinearClassifier): """ A subclass that uses the Multiclass SVM loss function """ def loss(self, X_batch, y_batch, reg): return svm_loss_vectorized(self.W, X_batch, y_batch, reg)
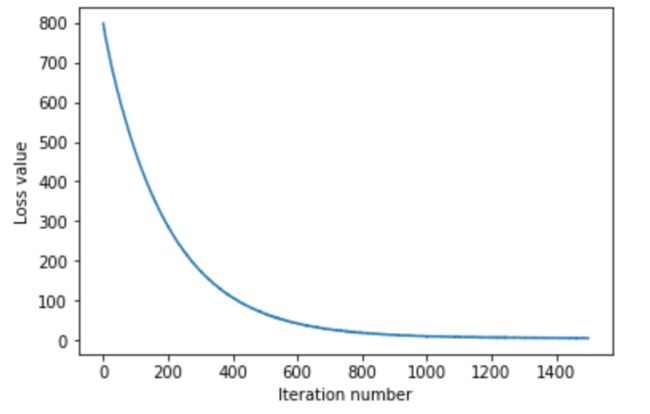
每次随机取出200个数据，训练1500次。 下图显示，损失值随着训练的迭代，追减降低。
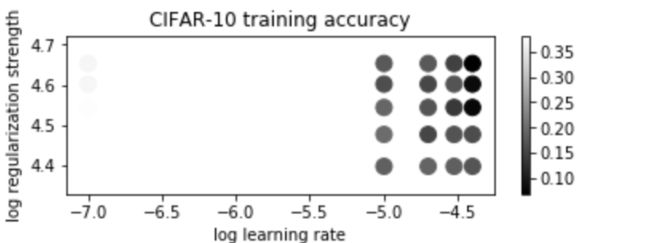
对于CIFAR-10的训练集和验证集的准确度如下。
training accuracy: 0.377939
validation accuracy: 0.383000
原文中还对学习率和Regulariztion Strength（不知道如何翻译好）做了各种调整。下面是各种组合的准确率统计。
颜色越深，表示准确率越高。可以看出来较低的学习率，训练的准确率越高。但是学习率越低，训练的时间也就越长。这是一个需要权衡的地方。
下图是最终训练出来的W所对应的图片。从图中可以看出最终的W，通过5万张图的训练， 提取出了具有指定分类的特征。
python相关：
- np.mean(a, axis=None)，
- 计算平均值。 axis=0，对整列计算均值。
- np.hstack(tup)，
- 在水平方向上合并
- np.vstack(tup),
- 在竖直方向上合并
- np.stack(arrays, axis=0),
- 增加了一个维度，而且合并的两个的形状必须一样。
- np.tile(A, reps)，
- A是被重复的对象，reps是在不同维度上重复的次数
- np.random.randn，
- [0,1)范围内的随机数，满足高斯分布
- tuple([randrange(m) for m in x.shape])，
- 随机选择x中的任意位置
- f = lambda w: svm_loss_naive(w, X_dev, y_dev, 0.0)[0]，
- lambda函数，w是参数，：后面是函数体。
- np.random.choice(a, size=None, replace=True, p=None)，
- 从a中随机选择size个数。replace=True，表示随机取出的数，还要放回去。
- np.max(a, axis=None, out=None, keepdims=np._NoValue)，
- 取最大值，也可以取每行或者每列中的最大值。
- np.argmax，
- 和np.max类似，区别是返回的是索引。
Reference：
1、知乎CS231n中文版，https://zhuanlan.zhihu.com/p/20918580?refer=intelligentunit